Задание 1. Решение систем линейных алгебраических уравнений.

Цель задания.

Практика в использовании численных методов решения систем линейных алгебраических уравнений.

Содержание задания.

1. Изучение численных методов решения систем линейных алгебраических уравнений.

2. Решение задачи, связанной с решением систем линейных алгебраических уравнений.

Постановка задачи.

Решить систему алгебраических уравнений вида

Ax=b (1)

де -невырожденная квадратная матрица порядка m,

- вектор-столбец правых частей системы. По найденному решению получить вектор невязок правой части системы.

порядок матрицы m , сама матрица A, вектор b и численный метод определяются вариантом задания (см. Приложение 1).

Требование к программе.

1. Алгоритм решения системы линейных алгебраических уравнений

должен быть оформлен в виде описания процедуры.

2. В качестве результатов программа должна выдать на печать решение системы, вектор невязок и - для итерационных методов - количество сделанных итераций.

Содержание отчета.

1. Постановка задачи для конкретного варианта.

2. Текст программы.

3 Полученные на ЭВМ результаты решения задачи.

Приложение 1. Варианты задания

I. Численный метод решения системы уравнений.

1.Первая модификация метода Гаусса.

Запишем исходную систему (1) в виде

(i=1,2,...m). (1')

Здесь .

Суть первой модификации метода Гаусса состоит в приведении системы (1') последовательным исключением неизвестных к треугольному виду:

(i=1,2,...m). (2)

из которой последовательно находятся (k=m,...,1).

Для применимости этого метода надо, чтобы значения элементов, на которые производится деление при исключении неизвестных, были отличны от нуля.

2.Вторая модификация метода Гаусса.

Суть второй модификации метода Гаусса состоит в том, чтобы привести систему уравнений вида (1') к треугольному виду (2), воспользовавшись представлением матрицы А в виде произведения A=CD, где C-левая, а D-правая треугольные матрицы, причем диагональные элементы матрицы D равны единице.

Элементы этих матриц вычисляются по рекуррентным соотношениям:

при

(3)

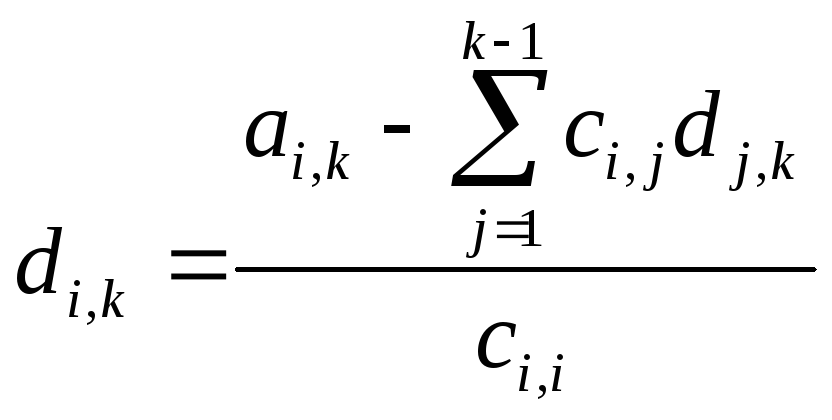при

Эти вычисления производятся последовательно для совокупностей

(i, k)=(1,1),...,(1,m)(2,1),...,(2,m),...,(m,1),...,(m, m).

Примечание. Здесь и далее в этом методе считается, что если верхний предел суммирования меньше нижнего, то вся сумма равна нулю.

После разложения матрицы А решение исходной системы сводится к последовательному решению двух систем с треугольными матрицами:

Cd=b Dx=d, (4)

где .

Заметим, что значение , которые являются решением системыCd=b, могут вычисляться одновременно с остальными по формулам (3), для чего эти вычисления проводятся последовательно для совокупностей

(i, k)=(1,1),...,(1,m+1),(2,1),...,(2,m+1),...,(m,1),...(m,m+1).

Значения (решение системыDx=d) находятся из соотношений

(i=m,m-1,...,1)

Для осуществления вычислений по формулам (3) необходимо, чтобы все были отличны от нуля; для этого необходимо и достаточно выполнение условий

(k=1,2,...,m-1) (5)

где - матрица главного минораk-го порядка матрицы А.

3.Метод ортогонализации.

Запишем исходную систему (1) в виде

. . . . . . . . . . . . (6)

где .

Иначе:

(здесь ). Таким образом, решение исходной системы равносильно нахождению вектораy с последней компонентой равной единице, ортогонального к векторам . Если добавить вектор, то векторылинейно независимы, поскольку определитель матрицы, строками которой они являются, равен.

С помощью алгоритма последовательной ортогонализации с нормировкой систему векторовможно привести к ортонормированной системе векторов:

, (k=1,2,...,m-1).

Вектор ортогонален ко всем векторампричем. Следовательно,- решение исходной системы. Метод ортогонализации применим при любой невырожденной матрицеA.

4.Метод простой итерации.

В методе постой итерации система (1) приводится к виду

(это можно сделать, например, так: x=x-D(Ax-b); если , то эта система эквивалентна системе (1); если в качествеD взять единичную матрицу, то C=E-A и g=b).

Решение системы (7) находится предел последовательности , получающейся из рекуррентных соотношений

При некотором начальном приближении . Обозначим. Тогда заданная точностьсчитается достигнутой, если.

Варианты норм векторов:

4.1) ;

4.2) ;

4.3)

Метод простой итерации сходится при любом начальном приближении (в качествеможно взять, например,g), если , а в качестве нормы матрицы можно взять, например,

5) Метод Зейделя.

В методе Зейделя последовательно уточняются компоненты решения исходной системы (1), причем k -я компонента находится из k -го уравнения. Именно, если , то следующее приближение определяется из системы соотношений:

. . . . . . . . . . . . . . . . (8)

Метод Зейделя сходится при любом (например,=b ), если для всех i выполняется условие

, где q<1

Считать, что требуемая точность достигнута, если

В качестве вариантов нормы вектора использовать те же нормы, что и в методе простой итерации (см. 4.1, 4.2 и 4.3).

II. Система уравнений.

Порядок системы m =5; для итерационных методов ; номерN системы - от 1 до 18: система с номером N=3(k-1)+l (k=1,2,...,6; l=1,2,3) задается матрицей и соответствующим вектором - правой частьюиз табл. 1 (все значения считаются точными).

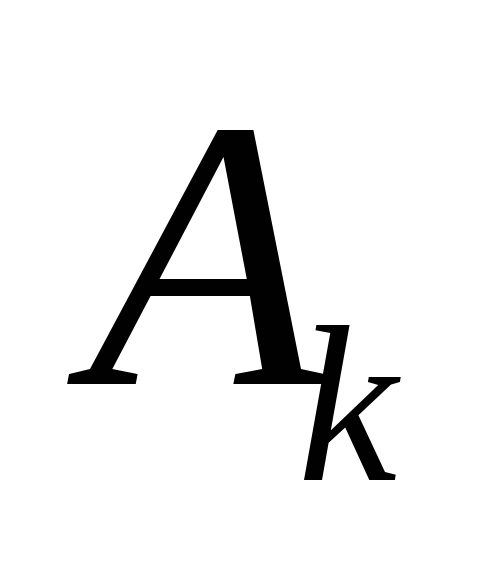
	i	J
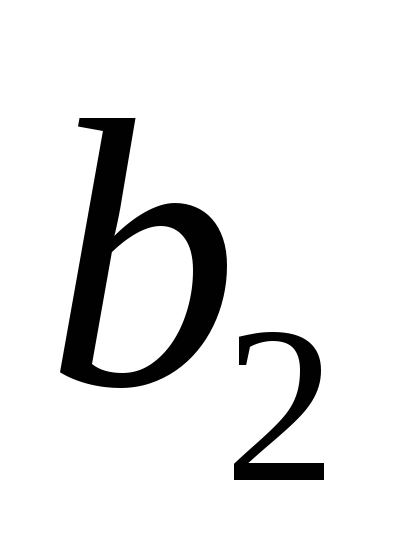
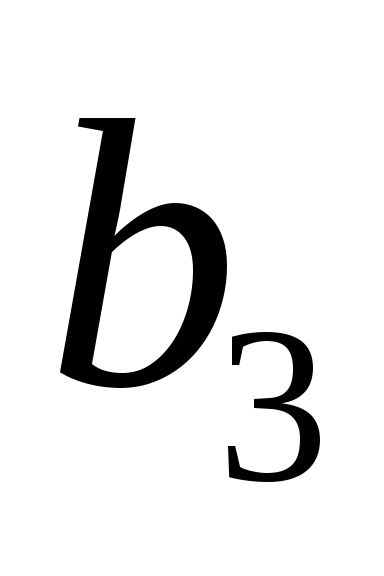
		1 2 3 4 5
	1 2 3 4 5	.45 .03 -.01 .02 -.111 .02 .375 -.01 .01 0 0 .07 .44 0 .113 - -.03 . 015 -.02 .41 -.084 .02 01 0 0 .29	-.275 -.78 1.75 -2.18 1.45	-1.784 .68 1.032 -1.056 1.12	2.491 1.275 -.783 .429 -.16
	1 2 3 4 5	.38 -.05 .01 .02 .07 .052 .595 0 -.04 .04 .03 0 .478 -.14 .08 -.06 .126 0 .47 -.02 .25 0 .09 .01 .56	-2.14 1.833 1.736 -1.242 1.44	.75 -.858 3.16 -1.802 2.91	2.32 2.544 -3.238 1.534 .12
	1 2 3 4 5	.405 .05 .04 0 .09 -.061 .53 .073 .11 -.06 .07 -.036 .38 .03 .02 -.05 0 .066 .58 .23 0 .081 -.05 0 .41	-1.475 2.281 .296 .492 1.454	1.065 0.975 -1.312 1.096 -.048	1.77 -.53 -.626 -2.772 1.001
	1 2 3 4 5	.43 .045 -.02 .03 -.02 .12 .37 .02 0 -.01 .01 .032 .356 -.02 .05 .12 -.11 0 .49 .112 -.05 0 .025 -.01 .294	.457 -.86 1.718 .864 2.068	2.56 2.77 -.916 .808 -.639	.78 -.38 1.91 -1.464 2.362
	1 2 3 4 5	.49 0 -.128 .09 .15 -.03 .32 0 -.061 .02 .01 -.09 .58 .011 .035 .03 0 -.073 .58 0 .02 -.03 .145 -.012 .42	.964 1.279 -1.799 -4.971 2.153	1.564 -1.733 1.393 1.744 -2.046	2.332 -2.261 -1.484 .932 1.758
	1 2 3 4 5	.51 -.074 .01 -.13 .09 .08 .3 -.036 0 .05 15 0 .42 .06 -.07 .19 .023 .06 .438 0 .05 -.07 .023 0 .36	.708 2.578 -.19 1.64 -2.229	-.214 1.866 .18 -3.258 2.762	2.866 .842 -.75 -1.527 1.164