
МЖиГ (Вся теория)
.pdf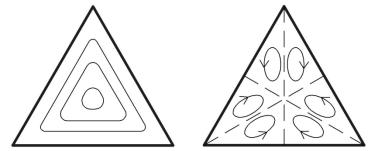
Для транспорта жидкостей в ряде случаев используются трубопроводы некруглого сечения. В таких трубах возникает сложная структура потока, в частности вторичные течения. Рассмотрим пример.
На Рис. 5.11 для треугольного сечения показаны линии равных скоростей и вторичные течения в плоскости поперечного сечения трубы. Накладываясь на продольное движение, вторичное течение непрерывно переносит количество движения по направлению к углам, в результате чего в угловых участках наблюдаются сравнительно высокие продольные скорости.
Рис. 5.11. Линии постоянных скоростей (изотахи) и вторичные течения в треугольной трубе
Такого рода структуры потока можно получить и для других некруглых сечений, используя компьютерные технологии. Зная профиль скоростей, можно определить коэффициенты гидравлического сопротивления и, как следствие, потери напора.
Однако в инженерной практике применяется более простое приближенное решение: для определения потери напора в некруглых трубах применяется формула Дарси
– Вейсбаха. В этой формуле в качестве диаметра трубы используется эквивалентный диаметр:
Здесь λ f Re,
|
|
h λ |
l |
|
w2 |
. |
(5.48) |
|||
|
|
|
|
|
||||||
|
|
l |
|
dэкв |
|
2g |
|
|||
|
|
|
|
|
|
|
||||
|
, |
Re |
wdэквρ |
.. |
|
|
|
|
||
|
|
|
|
|
|
|||||
dэкв |
|
|
μ |
|
|
|
|
|||
Для расчета коэффициента гидравлического трения используются те же формулы, которые были приведены раньше для круглого сечения.
Таким образом, при гидравлическом расчете некруглых трубопроводов используется тот же алгоритм расчета, что и для круглых трубопроводов, но вместо диаметра принимается эквивалентный диаметр.
Для равностороннего треугольника разница между результатами точного решения и приближенного составляет не более 10 .
5.6.Определение оптимального диаметра трубопровода
При проектировании трубопроводных систем часто возникают проблемы определения оптимального диаметра трубопровода dопт . Предположим, что известны
Vɺ, z1, z2 ,l. Расчетные формулы:
81
w |
|
4Vɺ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||
|
πd |
2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
w2 |
|
l |
|
|
||||||
h1 2 hl hм |
|
|
|
|
|
|
|
|
λ |
|
ξ . |
||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2g |
|
d |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Для ламинарного режима: h |
|
|
~ |
1 |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 2 |
|
|
d4 |
|
|
|
|
|||||||||||
Для турбулентного режима: h |
|
|
~ |
|
|
|
1 |
|
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 2 |
|
|
|
|
d5 |
|
|
|
|
||||||||
Потребный напор системы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H z1 z2 h1 2. |
|
|
|||||||||||||||||
Мощность потока: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
ɺ |
|
|
|
|
|
|
|
|
|
|
||||
ρgVH. |
|
|
|
|
|||||||||||||||
Мощность насоса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
N |
|
|
, |
|
|
|
|
|||||||
н |
|
η η |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
эд |
|
|
|
|
||||||||||
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
||||||
(5.49)
(5.50)
(5.51)
(5.52)
где ηн – КПД насоса, ηэд – КПД электродвигателя.
Оптимальный (наиболее экономически выгодный) диаметр dопт определяется на основе технико-экономических расчетов.
Уменьшение диаметра трубопровода приводит к увеличению мощности насоса Nн; увеличение d – наоборот к уменьшению Nн. Но увеличение диаметра приведет к увеличению стоимости трубопровода и строительства трубопроводной сети. Итак, необходимо учитывать как затраты эксплуатационные, так и капитальные. Эксплуатационные затраты Cэ : расход электроэнергии на работу насоса, обслуживание
трубопроводной сети, ремонт сети и управленческие расходы. Капитальные затраты Cк : стоимость насоса и трубопроводов, стоимость сооружений и амортизационные расходы.
Полная стоимость варианта трубопроводной сети: |
|
|||
C Cэ |
Cк |
|
(5.53) |
|
t |
||||
|
|
|||
где t – срок окупаемости сооружения. Обычно 7 t 10 лет. |
|
|||
Таким образом, задача определения оптимального диаметра |
трубопровода dопт |
|||
сводится к определению минимума полной стоимости трубопроводной сети С. Задача может быть решена разными методами:
–математический (определение минимума функции С);
–графический;
–подбор вариантов.
Математический метод – это задача однопараметрической оптимизации.
Определяем первую производную С по dопт |
и приравниваем её к нулю; оттуда находим |
||||
dопт . При этом вторая производная должна быть больше нуля. |
|
||||
|
dC |
0 , |
d2C |
0 . |
(5.54) |
|
ddопт |
ddопт2 |
|||
|
|
|
|
||
82

Графический метод. Строим зависимости Cэ d и Cк d , складываем ординаты при одинаковых d, находим минимум С (Рис. 5.12).
Рис. 5.12. К определению оптимального диаметра трубопровода
Подбор вариантов. Для капельной жидкости приемлемые скорости жидкости в трубопроводах колеблются в пределах w = 0,5÷3 м/с.
Найдем диаметры трубопроводов для скорости 0,5 м/с – d1 и 3 м/с – d2 . Определим
C1 и C2 . Cmin будем искать в пределах от d1 до d2 . Далее, идя навстречу друг другу, по
диаметру найдем Cmin и dопт .
По терминологии экономистов полная стоимость варианта трубопроводной сети С
– приведенная годовая затрата.
5.7.Течение в трубах неньютоновских жидкостей
Рассмотрим горизонтальную цилиндрическую трубу круглого сечения.
Аномально-вязкие жидкости.
Для круглой трубы распределение напряжений трения определяется по формуле:
τ p r. (5.55) 2l
Принимая реологическое уравнение аномально-вязкой жидкости в виде степенной зависимости (5.55) получим:
|
dw m |
|
p |
|
|
|
|
||||||||||
|
K |
|
|
|
x |
|
|
r. |
|
|
|
(5.56) |
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
dr |
|
2l |
|
|
|
|
|||||||||
Здесь K и m – реологические константы жидкости, p – потери давления на участке |
|||||||||||||||||
длиной l. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегрирование уравнения |
(5.56) |
|
при граничном условии r R , |
wx 0 дает |
|||||||||||||
распределение скорости по сечению трубы в следующем виде: |
|
||||||||||||||||
|
1 |
|
|
|
|
|
|
m 1 |
|
|
m 1 |
|
|
||||
|
p |
|
m |
|
|
|
|
||||||||||
m |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||
wx |
|
|
|
|
|
|
R m |
r m . |
(5.57) |
||||||||
|
|
||||||||||||||||
|
2Kl |
|
m 1 |
|
|
|
|
|
|
|
|
||||||
Максимальная скорость достигается на оси трубы при r 0. Средняя скорость получена в виде:
83

|
|
|
|
1 |
|
m 1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
p m |
|
|
|||||
|
|
|
|
|||||||
wx cp |
|
|
|
|
R |
m |
. |
(5.58) |
||
|
|
|||||||||
|
|
3m 1 |
2Kl |
|
|
|
||||
Согласно формуле (5.58) потеря давления p ~ wxm . Это означает, что p для псевдопластичных жидкостей растет медленнее с ростом wx , чем для ньютоновских, а для дилатантных – быстрее (Рис. 5.13).
Рис. 5.13. Распределение обобщенных скоростей по сечению трубы: 1 – ньютоновская жидкость; 2 – псевдопластичная жидкость; 3 – дилатантная жидкость
Используя формулу (5.58), можно определить расход жидкости при известных свойствах жидкости и параметрах течения. В случае необходимости из (5.58) можно найтиp.
Вязко-пластическая среда. Эта среда обладает предельным напряжением сдвига τ0 . Если напряжение трения τ τ0 , то течения среды не будет. Для реализации течения необходимо, чтобы τ τ0 (Рис. 5.14).
В области |
τ τ0 возникает пристенное кольцевое течение. В центральной части |
трубы, при τ τ0 |
среда будет двигаться как твердый стержень с одинаковой скоростью |
wxc . |
|
Рис. 5.14. Схема течения вязко-пластичной среды
Итак, имеем следующие исходные зависимости:
При τ τ0 |
dwx |
0 ; при τ τ0 |
|
|
|
dwx |
|
|
τ0 |
μ |
|
|
|||
dr |
dr |
||||||
|
|
|
|
|
Для кольцевой зоны получена формула: |
|
|||||||||
|
|
1 |
|
p |
R |
2 |
|
2 |
τ0 |
|
wx |
|
|
|
|
|
r |
|
R r .. |
||
μ |
4l |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
Для осевой (стержневой) зоны:
84
p r.
2l
(5.59)
(5.60)
|
|
|
1 |
p |
R |
2 |
2 |
τ0 R r0 |
|
|
|
|||||||
|
wxc |
|
|
|
|
|
|
r0 |
. |
(5.61) |
|
|||||||
|
|
μ |
|
|
|
|||||||||||||
|
|
|
|
4l |
|
|
|
|
|
|
|
|
|
|
|
|
||
Общий объемный |
расход |
складывается |
из |
потоков |
стержневой зоны Vɺ |
и |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ст |
|
кольцевой зоны Vɺ |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
Vɺ Vɺст |
Vɺк |
wxc πr02 |
wx 2πrdr. |
(5.62) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r0 |
|
|
|
|
|
После ряда упрощений формула (5.62) принимает вид: |
|
|
||||||||||||||||
|
|
|
|
|
|
pπR4 |
|
|
8 |
|
τ |
l |
|
|
|
|
||
|
|
|
Vɺ |
|
|
|
1 |
|
|
0 |
|
. |
|
(5.63) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
8μl |
|
|
|
3 |
|
pR |
|
|
|
|||
Формула (5.63) является аналогом уравнения Пуазейля. Она может быть использована и для определения потери давления p .
Вязко-пластические среды иногда называют бингамовскими жидкостями или телами Шведова – Бингама.
85

Глава 6. Истечение жидкостей через отверстия и насадки
В инженерной практике часто приходится иметь дело с истечением жидкости через отверстия различной формы и размеров, а также через короткие трубки (патрубки), называемые насадками.
Отверстием в тонкой стенке называют такое отверстие, края которого имеют острые кромки и толщина стенки не влияет на форму и условия истечения струи (Рис. 6.1). При этом возникают только местные сопротивления (внезапное сжатие). Частицы жидкости приближаются из всего прилегающего объема по плавным траекториям. Струя отрывается от стенки у кромки отверстия и затем по инерции несколько сжимается. Максимальное сжатие наблюдается на расстоянии от стенки резервуара, примерно равном диаметру отверстия d (dс – диаметр максимального сжатия струи). Наиболее существенна инерционность частиц, двигающихся к отверстию вдоль стенки; они огибают край отверстия и образуют внешнюю поверхность струи на участке сжатия. Если отверстие не круглое, а, например, квадратное или треугольное, то наблюдается явление инверсии струи, т.е. изменение формы ее поперечного сечения. Например, струя, вытекающая из квадратного отверстия, приобретает на некотором расстоянии крестообразную форму. Это объясняется действием сил инерции и поверхностного натяжения.
Сжатие струи оценивается коэффициентом сжатия ε, определяемым как Sc .
S
Рис. 6.1. Схема истечения через отверстие в тонкой стенке
6.1. Истечение жидкостей через отверстия в тонкой стенке при постоянном напоре
Наиболее важными параметрами процесса истечения для инженерной практики являются скорость истечения и расход жидкости. Определить эти параметры можно, используя уравнение Бернулли для установившегося движения потока жидкости (когда H = const). Выберем плоскость сравнения 0 - 0 и запишем уравнение Бернулли для сечений 1
– 1 и 2 – 2 с учетом того, что сечение 1 – 1 много больше площади сечения 2 – 2, что, в соответствии с уравнением неразрывности w1 << w2 позволяет пренебречь скоростным
86

напором (сечение 1 - 1 – свободная поверхность жидкости в резервуаре, сечение 2 - 2 – сжатое сечение струи – Рис. 6.1):
|
p |
|
p |
w2 |
|
|
||
H |
атм |
0 |
0 |
атм |
|
с |
h |
(6.1) |
|
|
|
||||||
|
g |
|
g |
2g |
м |
|
||
|
|
|
|
|||||
Решаем уравнение относительно wc – скорости струи в сжатом сечении. С учетом того, что
h |
|
|
|
w2 |
|
|
c |
(6.2) |
|||
|
|
||||
м |
|
c |
|
2g |
|
где ξc –коэффициент местного сопротивления при внезапном сужении потока, находим:
|
|
w |
1 |
|
|
|
|
|
||||
|
|
|
|
2gH |
(6.3) |
|||||||
|
|
|
|
|||||||||
|
|
c |
1 c |
|
||||||||
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
||||
Если обозначить |
|
|
|
|
как |
коэффициент скорости истечения, то |
||||||
|
|
|
|
|||||||||
1 c |
||||||||||||
|
|
|
|
|
|
|
|
|||||
wc 
 2gH
2gH
Для идеальной жидкости ξc = 0 и φ = 1, откуда получаем формулу Торичелли:
wT |
|
2gH |
|
(6.4) |
|||||
Определим расход потока: |
|
|
|
|
|
|
|
|
|
Vɺ w S |
|
|
|
|
|
|
|
|
|
c |
|
|
|
2gH S, |
(6.5) |
||||
c |
|
|
|
|
|
|
|
|
|
т.е. |
|
|
|
|
|
|
|
|
|
Vɺ S |
|
|
|
(6.6) |
|||||
|
2gH , |
||||||||
где μ = ε · φ – коэффициент расхода.
Для инженерных расчетов обычно принимают следующие значения коэффициентов: ε = 0,64; φ = 0,97; μ = 0,62.
Следует отметить, что данные значения справедливы для турбулентного режима течения, а в общем случае все эти коэффициенты зависят от критерия Рейнольдса.
6.2.Истечение жидкостей через насадки. Виды и назначение насадков
Параметры струи, вытекающей через отверстия, можно изменять в определенных пределах, используя насадки. Насадки бывают цилиндрические, конические и коноидальные. Рассмотрим схему работы цилиндрического насадка (Рис. 6.2).
87
Рис. 6.2. Схема истечения через цилиндрический насадок
При входе струи в насадок она сжимается так же, как и при истечении из отверстия в тонкой стенке, а затем расширяется, заполняя на выходе все сечение насадка. В результате между поверхностью транзитной струи и поверхностью насадка образуется кольцевая вихревая зона, а на выходе из насадка Sc = S, т.е. εнас = 1.
При этом оптимальная длина насадка ℓ, в пределах которой выполняются эти соотношения, обычно находится в пределах (3÷4)d.
При составлении уравнения Бернулли для сечений потока на свободной поверхности жидкости в резервуаре и в выходном сечении насадка можно применить алгоритм, уже использованный для отверстия в тонкой стенке, но с соответствующими поправками на потери напора в результате расширения струи и ее движения по насадке (короткому трубопроводу) длиной ℓ. В этом случае скорость истечения запишется:
|
|
|
|
2gH |
|
|
|
|
|
|
|
|
|
|
|
|
||
wнас |
|
|
|
|
|
|
|
нас 2gH |
(6.7) |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
ℓ |
||||||||||
1 |
c |
|
p |
|
|
|
|
|
|
|
|
|
|
|
||||
d |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нас |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.8) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
ℓ |
|
|
|
||||||
|
|
|
|
c |
p |
d |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
c – коэффициент местного сопротивления сужения, |
|
|||||||||||||||||
p – коэффициент местного сопротивления расширения,
λ– коэффициент сопротивления по длине потока.
Из формулы следует, что коэффициент скорости для насадка меньше, чем для отверстия в тонкой стенке за счет того, что увеличиваются потери энергии на расширение струи и трение о стенки насадка. Поэтому скорость истечения также уменьшается. Для инженерных расчетов обычно принимают φнас. = 0,8 ÷0,82 откуда μнас. = φнас.· εнас.= 0,8 · 1 = 0,8.
Сравнение μотв и μнас показывает, что расход через насадок при прочих равных условиях больше, чем через отверстие в тонкой стенке. С одной стороны, наличие насадка увеличивает гидравлическое сопротивление, с другой стороны – расход увеличивается. Кажущийся парадокс можно объяснить следующим эффектом. При сравнении параметров струи в узком (сжатом) сечении и в широком (выходном) замечаем, что Sвых> Sс, значит, и wвых < wc (следует из уравнения неразрывности потока). Из уравнения Бернулли следует, что рвых > рс, но рвых = рат, поэтому рс < рaт. Таким образом, в сжатом сечении образуется вакуум, который служит дополнительной движущей силой для движения струи, увеличивая расход.
Конические и коноидальные насадки можно объединить в группу
нецилиндрических насадков.
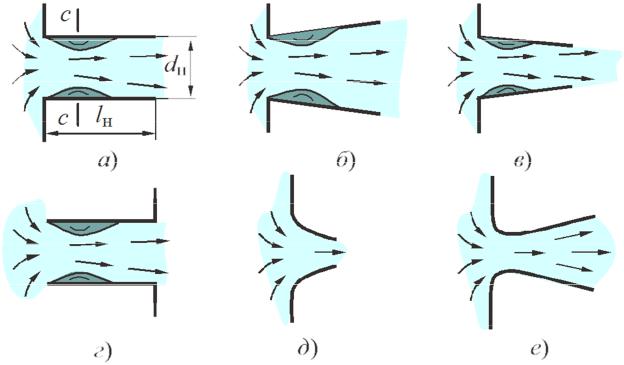
При этом конические насадки (Рис. 6.3) подразделяются на расходящиеся (б) и сходящиеся (в). Сходящиеся насадки увеличивают скорость и дальнобойность струи, расходящиеся насадки обеспечивают увеличение расхода. Коноидальный насадок (д-е) – частный случай конического, форма которого соответствует форме вытекающей струи
88
(плавное сужение). При этом вихреобразование почти не возникает, коэффициент расхода приближается к единице.
Рис. 6.3. Виды насадков: а,г – цилиндрический; б – конический расходящийся; в – конический сходящийся; д-е – организация плавного входа
6.3. Истечение жидкостей через отверстия и насадки при переменном напоре
Истечение жидкости из резервуара при переменном напоре является примером неустановившегося движения (скорость истечения и расход меняются во времени). Поэтому применение уравнения Бернулли в обычной форме (для установившегося движения) является, строго говоря, неправомерным. Однако в резервуарах большого размера напор изменяется очень медленно и в течение малого отрезка времени напор можно считать постоянным. В рассматриваемом примере (Рис. 6.4) напор уменьшается с величины Н1 до величины Н2, а его текущее переменное значение обозначается как Н. Через время dt напор уменьшается на величину dH, объём жидкости в резервуаре изменяется на величину dV = - Ω · dH, где Ω - площадь сечения резервуара (обычно Ω = const), а dH – отрицательная величина, поскольку Н уменьшается с течением времени.
89

Рис. 6.4. Схема истечения при переменном напоре
Изменение объёма dV можно также определить, считая, что за время dt напор Н изменяется незначительно и используя полученную ранее формулу для определения расхода при постоянном напоре:
|
|
|
dV Q dt S |
2gH dt |
|
После приравнивания двух выражений для dV:
S
 2gH dt dH
2gH dt dH
Ив результате разделения переменных получаем:
dt |
|
|
|
dH |
||
S |
|
|
|
|
||
|
|
2g |
|
|
H |
|
После интегрирования в пределах от Н1 до Н2:
|
H2 |
|
|
|
|
|
|
dH |
|
|
|||
t |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
S |
2g |
|
|
|
|
|
|||||||
|
H |
|
|
|
H |
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Откуда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
|||
|
|
H1 |
|
H2 |
|||||||||
|
|
|
|
|
|||||||||
|
|
|
|
||||||||||
|
S 2g |
|
|
|
|
|
|
|
|
||||
(6.9)
(6.10)
(6.11)
(6.12)
(6.13)
Для определения времени полного опорожнения резервуара (Н2 = 0) умножим числитель и знаменатель на 
 H1 и получим:
H1 и получим:
t |
2 |
H |
1 |
|
|
|
H |
1 |
|
2 H |
1 |
|
|
|
2V |
(6.14) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɺ |
|||||
S |
|
|
|
|
|
|
|
|
|
|
S 2gH |
|
|||||||||
|
|
2g |
|
H |
1 |
|
|
1 |
|
|
V |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
||||
где V – рабочий объём резервуара (до центра отверстия), Vɺ |
– максимальный |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
расход жидкости при истечении через отверстие (при Н = Н1).
90
