МЖиГ (Вся теория)

Шкалы абсолютных и избыточных давлений являются неограниченными, шкала вакуума ограничена – она меняется от атмосферного давления до нуля.

Для измерения гидростатического давления применяются различные приборы. Их можно подразделить на две основные группы: жидкостные и механические.

Простейший жидкостной прибор – пьезометр (Рис. 2.4).

Пьезометр – открытая с обоих концов стеклянная трубка, которая одним концом

Вместо ртути могут быть использованы другие жидкости, плотность которых гораздо выше плотности жидкости, находящейся в резервуаре.

Для измерения перепада давления применяются жидкостные дифференциальные манометры (Рис. 2.6).

22

Рис. 2.6. Ртутный дифференциальный Рис. 2.7. Измерение вакуума манометр

Используется следующая формула для измерения разности давлений:

Обычно hрт называют вакуумметрической высотой и обозначают hвак.

Жидкостные манометры просты по конструкции, характеризуются большой точностью измерений, однако они применяются для измерения сравнительно небольших давлений. Для измерения больших давлений применяются механические манометры (Рис. 2.8). В механических манометрах жидкость измеряется величиной деформации гибкого элемента (полой пружины, мембраны). Механические манометры могут применяться и для измерения малых давлений и вакуума (моновакуумметры). Широкое распространение нашли сильфонные перепадомеры (Рис. 2.9), дифференциальные сильфонные манометры.

Рис. 2.8. Устройство пружинного Рис. 2.9. Сильфонный дифманометр манометра

2.4.Закон Паскаля и его использование в технике

23

Сначала рассмотрим силы давления жидкости на горизонтальные стенки.

Сила давления жидкости на горизонтальное дно сосуда определяется по формуле (Рис. 2.12):

Рис. 2.12. Сила давления жидкости на горизонтальные стенки

Рассмотрим более общий случай. Пусть площадь S расположена под углом α к горизонту и перпендикулярна к плоскости рисунка (Рис. 2.13).

Через проекцию контура площади S (линия АВ) проведем ось оу и спроектируем эту площадь на плоскость хоу.

Определим силу давления жидкости на элементарную площадку dS предполагая, что в пределах dy давление не меняется:

25

Рис. 2.13. Схема для определения силы давления жидкости на плоскую стенку

Последний интеграл в правой части уравнения представляет собой статический

плоскую стенку равна произведению площади стенки на гидростатическое давление в

Зная величины Р0 и Ризб , и точки их приложения, можно по правилам механики найти величину и точку приложения общей силы P.

2.6.Сила давления жидкости на криволинейные стенки. Закон Архимеда

В отличие от плоской стенки, элементарные силы, действующие на элементарные площадки криволинейной стенки в различных точках, различаются не только по величине, но и по направлению. Поэтому силу гидростатического давления, действующего на криволинейную стенку, непосредственно определить невозможно, его находят через составляющие (проекции) этой силы.

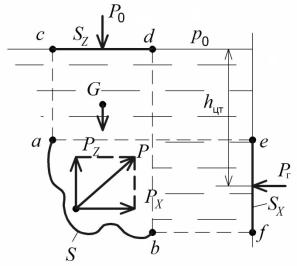
Для простоты рассмотрим цилиндрическую поверхность аb с образующей, перпендикулярной к плоскости чертежа (Рис. 2.14). Жидкость действует на стенку аb с силой Р , а стенка аb с такой же силой, но в обратную сторону. Разложим эту силу Р на

вертикальную Рz и горизонтальную Рх составляющие.

Далее рассмотрим условие равновесия объема жидкости, заключенного в

горизонтальную (свободную) поверхность, V – объем жидкого тела. Объем жидкого тела (тело давления) ограничено снизу криволинейной поверхностью аb, сверху – проекцией этой поверхности на свободную поверхность cd, а с боков – цилиндрической поверхностью, полученной в результате проектирования площади S на свободную поверхность. Необходимо отметить, что V не всегда представляет объем жидкости.

Рис. 2.14. Схема для определения силы давления жидкости на криволинейную (цилиндрическую) стенку

Определим горизонтальную составляющую Px . На некотором расстоянии по горизонтали от площади S жидкость условно разрезаем в вертикальной плоскости и правую часть отбрасываем. На вертикальную стенку спроектируем площадь S и получим

Sх .

27

Реакцию отброшенной части жидкости обозначим через Рг . Далее рассмотрим равновесие объема жидкости, заключенной между плоскостями аb и ef. Заметим, что сила

Рг является силой давления на плоскую стенку Sх :

В этом случае Рz определяется по формуле (2.36), Рx – по формуле (2.37). Сила Ру

, как и сила Рx , расположена в горизонтальной плоскости и определяется по формуле, аналогичной (2.37).

Закон Архимеда. Рассмотрим полностью погруженное в жидкость твердое тело (Рис. 2.15).

Рис. 2.15. Тело, покоящееся в жидкости Горизонтальные составляющие силы Рх и Ру полностью уравновешиваются.

Рассмотрим вертикальную составляющую Рz .

Вертикальная сила, действующая на нижнюю поверхность аbс больше вертикальной силы давления на верхнюю поверхность adc. Разность вертикальных сил,

где Vтв – объем твердого тела, – плотность жидкости.

Итак, на тело, погруженное в жидкость, действует гидростатическая подъёмная сила, направленная вверх и численно равная силе тяжести вытесненной им жидкости. Точка приложения гидростатической подъемной силы – центр тяжести вытесненного объема жидкости.

2.7.Относительный покой жидкости

28

Относительным покоем жидкости называется случай её движения, при котором вся масса жидкости движется как твердое тело, отдельные её части не смещаются одна относительно другой.

Рассмотрим два случая.

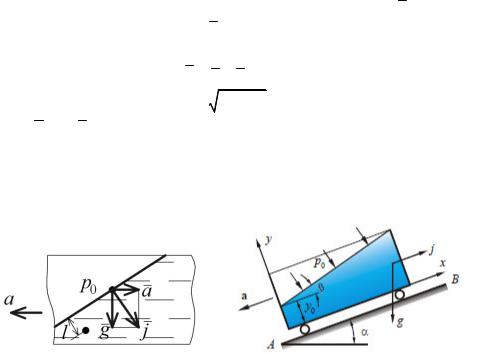
Случай первый. Сосуд с жидкостью движется прямолинейно и равноускоренно (Рис. 2.16).

Пусть сосуд движется с ускорением a. Сила инерции a направлена в сторону, обратную ускорению, сила тяжести g направлена вниз. Найдем направление и величину

равнодействующей массовой силы:

j a g,

(2.41)

j a2 g2 ,

где а и g – векторы единичных сил инерции и тяжести. Для всех частиц рассматриваемого объема жидкости равнодействующие массовые силы параллельны друг другу, а поверхности уровня перпендикулярны к этим силам, в том числе и свободная поверхность.

Рис. 2.16. Схема относительного покоя жидкости

Давление в любой точке определяется по формуле:

плотность жидкости, l – расстояние по нормали от точки до свободной поверхности. Если a 0, то j g , и уравнение (2.42) превратится в основное уравнение гидростатики.

Случай второй. Сосуд равномерно вращается вокруг вертикальной оси с угловой скоростью ω (Рис. 2.17).

В данном случае массовыми силами являются сила тяжести и центробежная сила. Воспользуемся основным дифференциальным уравнением гидростатики (2.6):

29

Рис. 2.17. Равновесие жидкости во вращающемся сосуде

Для решения задачи перейдем к цилиндрической системе координат r, , z. Нетрудно доказать, что:

рассматриваемой точки А под свободной поверхностью. Подставляя значение h в уравнение (2.46), получим:

жидкости. Однако форма свободной поверхности, от которой отсчитывается глубина

где z является текущей координатой свободной поверхности.

Уравнение (2.48) описывает кривую в виде параболы, а свободная поверхность, полученная на основе этой кривой, является параболоидом вращения.

30