Закон джоуля-ленца (в интегральной и локальной формах). Мощность тока.

При прохождении тока через проводник, обладающий сопротивлением R, выделяется тепло (происходит нагрев проводника). Возможны два случая: однородного и неоднородного участка цепи. При определении количества этого тепла используется закон сохранения энергии и закон Ома. Рассмотрим однородный участок цепи, к концам которого приложено напряжение U. За время dt переносится заряд dq:

.

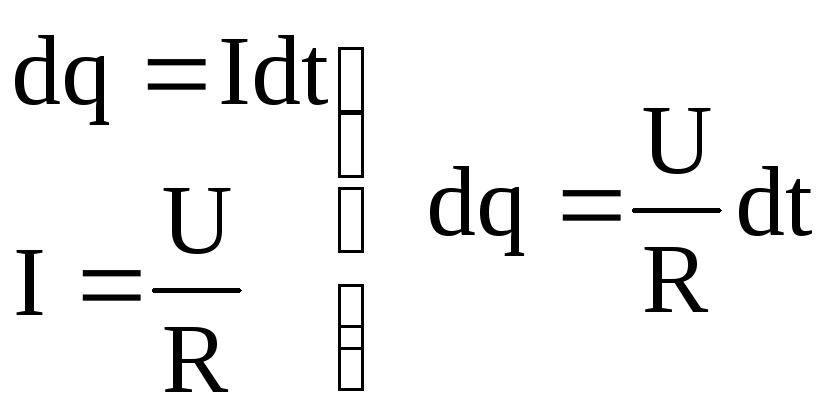Если в цепи нет , то U = ₁  ₂ и работа по переносу dq:

.

Согласно закону сохранения энергии должна выделяться внутренняя энергия (теплота), т.к. проводник неподвижен и не происходит химических превращений, эквивалентная этой работе: dQ = dA.

Таким образом:

,

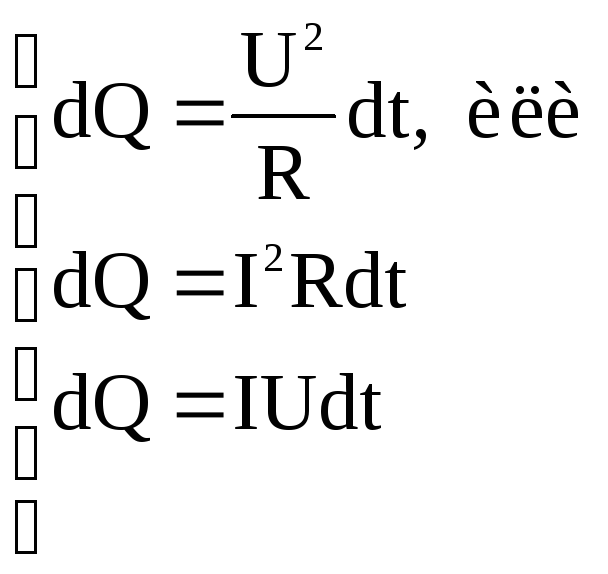получаем выражение, отражающее экспериментальный закон Джоуля-Ленца.

Полная теплота, выделившаяся за время :

.

Количество теплоты, выделившееся за единицу времени – тепловая мощность тока:

Это выражение так же отражает Закон Джоуля-Ленца в интегральной форме (т.к. мы идём от элементарного заряда dq и элементарной работы dA).

Чтобы получить выражение этого закона в дифференциальной форме, характеризующей выделение теплоты в различных местах проводящей среды, рассмотрим цилиндр элементарного объёма dV длины dl и площадью поперечного сечения dS. В этом объёме за время dt согласно закону Джоуля-Ленца выделится количество теплоты:

dQ = RI²dt=ρ (jdS)²dt= ρj²dVdt,

где dV = dSdl  объём цилиндра. Разделив это уравнение на dVdt, получим формулу, которая определяет количество теплоты, выделяющейся за единицу времени в единице объёма проводящей среды – удельную тепловую мощность тока:

P_уд=ρj²,

т.е. закон Джоуля-Ленца в дифференциальной форме.

Удельная тепловая мощность тока пропорциональна квадрату плотности электрического тока и удельному сопротивлению среды в данной точке. Это наиболее общая форма закона Джоуля-Ленца, применяемая к любым проводникам вне зависимости от их формы, однородности и природы сил, возбуждающих электрический ток.

Если на носители тока действуют только электрические силы, то на основании выражения j = E, мы получим частный случай для однородного участка цепи:

P_уд = = = E².

Рассмотрим неоднородный участок цепи, содержащий источник ЭДС. В этом случае действуют и сторонние силы, а не только электрические. Исходя из закона Ома для неоднородного участка цепи:

RI = φ₂  φ₁ + ε,

умножив обе части на I, видим, что:

RI² = (φ₂  φ₁)I + εI или P =(φ₂  φ₁)I + εI

выполняется закон сохранения энергии.

Слева в этом равенстве  тепловая мощность P, а справа алгебраическая сумма мощностей электрических и сторонних сил, которую называют мощностью тока на рассматриваемом участке цепи. Для цепи неразветвлённой (φ₂ = φ₁) и:

P = εI.

Общее количество выделяемой за единицу времени во всей цепи Джоулевой теплоты равно мощности только сторонних сил. Значит, теплота производится только сторонними силами, а электрическое поле перераспределяет эту теплоту по различным участкам цепи.

Для того чтобы получить запись закона Джоуля-Ленца в дифференциальной форме умножим обе части уравнения j = (E + E^*) на j, а также учтём, что = 1/ρ и ρj² = P_уд.. Тогда:

j²= j(E + E^*) => j² = j(E + E^*) => j² = j(E + E^*).

Окончательно записываем:

P_уд.= ρj²= j(E + E^*),

закон Джоуля-Ленца в дифференциальной форме в неоднородной проводящей среде.

11