
лекции по физике Родин / LEKTsIYa__10_TEOREMA_GAUSSA_DLYa_VEKTORA_V
.docЛЕКЦИЯ № 10
ТЕОРЕМА ГАУССА
ДЛЯ ВЕКТОРА
![]() .
ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА
.
ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА
![]() И ЕЁ ПРИМЕНЕНИЕ К РАСЧЁТУ ПОЛЕЙ.
И ЕЁ ПРИМЕНЕНИЕ К РАСЧЁТУ ПОЛЕЙ.
ПОЛЕ СОЛЕНОИДА.
В ажнейшие
свойства магнитного поля, как и
электрического, связаны с потоком и
циркуляцией векторного поля и выражают
основные законы магнитного поля.
ажнейшие
свойства магнитного поля, как и
электрического, связаны с потоком и
циркуляцией векторного поля и выражают
основные законы магнитного поля.
Потоком
![]() вектора магнитной индукции через
элементарную площадку
вектора магнитной индукции через
элементарную площадку
![]() (рис.5) называют скалярное произведение
(рис.5) называют скалярное произведение
![]() :
:
![]() .
.
Полный поток Ф через некоторую поверхность S равен:
![]() . (1)
. (1)
Теорема Гаусса:
Поток вектора
![]() сквозь любую замкнутую поверхность
равен нулю:
сквозь любую замкнутую поверхность
равен нулю:
![]() , (2)
, (2)
или в дифференциальной форме:
div
![]() = 0. (3)
= 0. (3)
Эта теорема выражает
тот факт, что силовые линии магнитного
поля замкнуты, поэтому число линий
вектора
![]() ,
выходящих из любого объема, всегда равно
числу линий, входящих в этот объем.
,
выходящих из любого объема, всегда равно
числу линий, входящих в этот объем.
Записанная в дифференциальной форме теорема Гаусса показывает, что в природе не существует магнитных зарядов, аналогичных электрическим зарядам, локализованным в пространстве.
Теорема о
циркуляции: для магнитного поля
постоянных токов циркуляция вектора
![]() по произвольному контуру L
равна произведению
по произвольному контуру L
равна произведению
![]() на алгебраическую сумму токов, охваченных
контуром (рис.6):
на алгебраическую сумму токов, охваченных
контуром (рис.6):
![]() , (4)
, (4)
г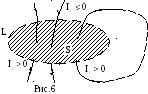 де
I = Ik,
причём Ik
величина
алгебраическая.
де
I = Ik,
причём Ik
величина
алгебраическая.
Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта. Ток противоположного направления считается отрицательным.
Для тока,
распределенного с какой-то плотностью
![]() ,
формула (4) принимает вид:
,
формула (4) принимает вид:
![]() . (5)
. (5)
Теорема о циркуляции может быть доказана из закона Био-Савара-Лапласа, но мы будем считать её как постулат, подтверждённый опытом.
Тот факт, что
циркуляция вектора
![]() означает, что поле вектора
означает, что поле вектора
![]() не потенциально
(в отличие
от поля
не потенциально
(в отличие
от поля
![]() ).
Такое поле называют вихревым
или соленоидальным.
).
Такое поле называют вихревым
или соленоидальным.
Теорема о циркуляции
вектора
![]() играет примерно ту же роль, что и теорема
Гаусса для векторов
играет примерно ту же роль, что и теорема
Гаусса для векторов
![]() и
и
![]() .
Вопрос в нахождении
.
Вопрос в нахождении
![]() можно решить при наличии симметрии,
сводя его к произведению B
(Bl)
на длину контура или его части.
можно решить при наличии симметрии,
сводя его к произведению B
(Bl)
на длину контура или его части.
ПРИМЕР.
Пусть постоянный ток I
течёт вдоль бесконечно длинного
проводника, имеющего круглое сечение
радиусом а.
Найти индукцию
![]() поля внутри и снаружи провода.
поля внутри и снаружи провода.
Р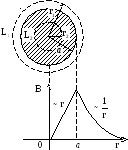 ешение
ешение
Из условия задачи
следует, что линии вектора
![]() в данном случае должны иметь вид
окружностей с центром на оси проводника.
Причем модуль вектора
в данном случае должны иметь вид
окружностей с центром на оси проводника.
Причем модуль вектора
![]() должен быть одинаков во всех точках на
расстоянии r
от оси проводника.
должен быть одинаков во всех точках на
расстоянии r
от оси проводника.
Из теоремы о
циркуляции вектора
![]() :
:
1) Снаружи проводника для контура L1: (r > a)
![]() ,
т. е.
,
т. е.
![]() и
и
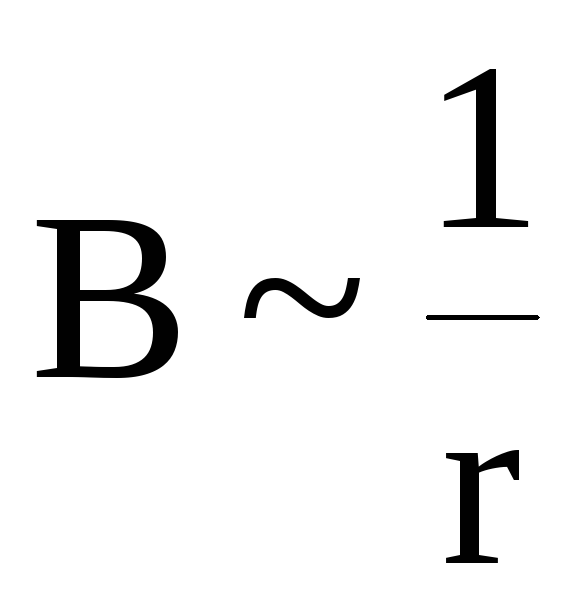 .
.
2) Внутри проводника для контура L2: (r < a)
![]() .
.
Выразим ток, охватываемый данным контуром I2 через данные в условии величины силу тока I и радиус а.
Так как плотность
тока j
= const
во всех точках проводника и
![]() ,
то для контура L2
и для проводника радиуса а
можно записать равенство
,
то для контура L2
и для проводника радиуса а
можно записать равенство
![]()
![]() .
Следовательно:
.
Следовательно: ![]() ,
т. е.
,
т. е.
![]() .
.
С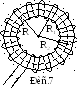 помощью закона полного тока можно найти
индукцию магнитного поля тороида.
помощью закона полного тока можно найти
индукцию магнитного поля тороида.
Тороидом называется
кольцевая катушка, имеющая форму тора,
на которую намотаны витки провода (рис.
7). Если витки расположены вплотную или
очень близко друг к другу, то тороид
можно приближенно рассматривать как
систему большого числа последовательно
соединенных круговых токов одинакового
радиуса, центры которых лежат на средней
линии тороида. Линии магнитной индукции
поля тороида имеют вид концентрических
окружностей радиуса r,
центры которых лежат на оси тороида.
Ось проходит перпендикулярно плоскости
радиуса через точку О.
Очевидно, что значения индукции
![]() во всех точках замкнутого контура L,
совпадающего с какой-либо линией индукции
магнитного поля тороида, одинаковы.
во всех точках замкнутого контура L,
совпадающего с какой-либо линией индукции
магнитного поля тороида, одинаковы.
Сказанное выше
позволяет применить закон полного тока
для индукции
![]() и определить ее значение внутри соленоида:
и определить ее значение внутри соленоида:
![]() .
.
Если
r
> R2
или r
< R1,
то Iохв
= 0, т.е. магнитное поле локализовано
внутри тороида. Для контура L радиуса
R1
< r
< R2
суммарная сила токов, охватываемых
контуром L, будет равна NI, где N – число
витков обмотки тороида, а I – сила тока
в ней. Приравнивая циркуляцию вектора
![]() в соответствии с законом (4) к величине
0NI,
получаем:
в соответствии с законом (4) к величине
0NI,
получаем:
![]() .
(6)
.
(6)
В случае тонкого тороида диаметр витков d = R2 – R1 мал по сравнению с радиусом средней (осевой) линии R = (R1 + R2)/2 и в пределах площади витка магнитное поле тороида можно приближенно считать однородным:
B B = 0NI/(2R) = 0nI, (7)
где n – число витков обмотки тороида, приходящихся на единицу длины осевой линии тороида (N = n2R).
Если неограниченно
увеличивать R,
сохраняя неизменным диаметр d
витков и
плотность n витков, то в пределе получится
бесконечно длинный соленоид. Поле внутри
такого соленоида однородно, так как
всюду векторы
![]() одинаково направлены и равны по модулю:
B
= 0nI.
Это соотношение также было получено
нами (рис.8) значительно более сложным
путем, основанным на использовании
принципа суперпозиции полей.
одинаково направлены и равны по модулю:
B
= 0nI.
Это соотношение также было получено
нами (рис.8) значительно более сложным
путем, основанным на использовании
принципа суперпозиции полей.
Соленоидом называется цилиндрическая катушка с током, состоящая из большого числа витков проводника, которые образуют винтовую линию. Если витки расположены вплотную или очень близко друг к другу, то соленоид можно рассматривать как систему последовательно соединенных круговых токов одинакового радиуса с общей осью.
Н а
рис. 8 показано сечение соленоида радиуса
R и длины L с током I.
а
рис. 8 показано сечение соленоида радиуса
R и длины L с током I.
Кружки с точками изображают сечения витков, в которых электрический ток направлен из-за чертежа к нам, а кружки с крестиками – сечения витков, в которых ток направлен за чертеж.
Рассмотрим магнитное
поле, создаваемое соленоидом. Пусть n –
число витков, приходящихся на единицу
длины соленоида, т.е.
![]() ,
N – общее число витков, L – длина соленоида.
В произвольной точке А, лежащей на оси
соленоида, магнитная индукция
,
N – общее число витков, L – длина соленоида.
В произвольной точке А, лежащей на оси
соленоида, магнитная индукция
![]() в силу принципа суперпозиции, равна
векторной сумме магнитных индукций
в силу принципа суперпозиции, равна
векторной сумме магнитных индукций
![]() полей всех витков этого соленоида.
полей всех витков этого соленоида.
В этой точке все
векторы
![]() и результирующий вектор
и результирующий вектор
![]() направлены по оси
направлены по оси
![]() в сторону перемещения буравчика с правой
резьбой при вращении его рукоятки в
направлении электрического тока в
витках соленоида. На малый участок
соленоида длиной dl
вдоль оси
приходится ndl
витков. Если
l
– расстояние вдоль оси от этих витков
до точки А, то согласно закона
Био-Савара-Лапласа магнитная индукция
поля этих витков
в сторону перемещения буравчика с правой
резьбой при вращении его рукоятки в
направлении электрического тока в
витках соленоида. На малый участок
соленоида длиной dl
вдоль оси
приходится ndl
витков. Если
l
– расстояние вдоль оси от этих витков
до точки А, то согласно закона
Био-Савара-Лапласа магнитная индукция
поля этих витков
![]() . (8)
. (8)
Так как r
= R/sin
и l
= R/tg,
то dl
найдем как дифференциал функции R/tg:
![]() .Тогда
.Тогда
![]() . (9)
. (9)
В пределах соленоида угол изменяется от 1 до 2, поэтому
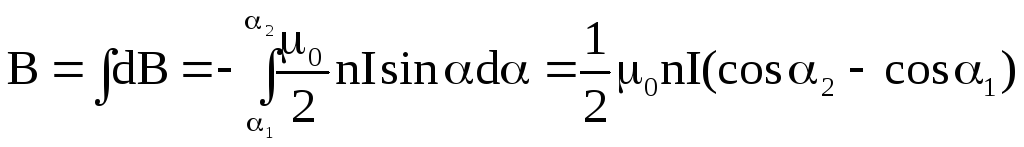 (10)
(10)
где
![]() . (11)
. (11)
Из соотношений
(10) и (11) видно, что магнитная индукция
поля соленоида в точке А зависит от силы
тока I,
густоты намотки витков n, радиуса R витков
и длины L
соленоида, а также от положения точки
А относительно концов соленоида. Можно
показать, что значение В максимально,
если l1
= L/2,
так что
![]() ,
тогда
,
тогда
![]() . (12)
. (12)
Если L >> R , то соленоид можно считать бесконечно длинным. Для точки А, лежащей вдали от концов такого соленоида, 1 0, 2 . Тогда в соответствии с формулой (10) имеем:
B = 0nI. (13)
Магнитный момент соленоида равен геометрической сумме магнитных моментов всех его N = nL витков:
![]() , (14)
, (14)
где
![]() – единичный вектор, направленный по
оси соленоида в ту же сторону, что и
вектор
– единичный вектор, направленный по
оси соленоида в ту же сторону, что и
вектор
![]() .
Модуль магнитного момента соленоида
.
Модуль магнитного момента соленоида
pm = nIV, (15)
где V = LS – объем соленоида.
ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА
ТЕОРЕМЫ О
ЦИРКУЛЯЦИИ ВЕКТОРА
![]() .
.
В дифференциальной
форме теорема Гаусса для вектора
![]() записывается в виде:
записывается в виде:
![]() или
или
![]() , (16)
, (16)
т. е. дивергенция
поля
![]() всюду равна нулю.
Это означает, что как мы уже отмечали,
магнитное поле не имеет источников
(магнитных зарядов), магнитное поле
порождают электрические токи. Закон
(16) является фундаментальным,
он справедлив не только для постоянных,
но и для переменных магнитных полей.
всюду равна нулю.
Это означает, что как мы уже отмечали,
магнитное поле не имеет источников
(магнитных зарядов), магнитное поле
порождают электрические токи. Закон
(16) является фундаментальным,
он справедлив не только для постоянных,
но и для переменных магнитных полей.
Для того чтобы
представить (записать) выражения (4, 5) в
дифференциальной форме введём понятие
ротора (вихрь) поля
![]() .
.
Рассмотрим отношение
циркуляции вектора
![]() к площади S,
ограниченной контуром. Оказывается,
что это отношение стремится к некоторому
пределу при S0,
причём этот предел зависит от ориентации
контура в данной точке пространства.
Ориентация контура задаётся вектором
к площади S,
ограниченной контуром. Оказывается,
что это отношение стремится к некоторому
пределу при S0,
причём этот предел зависит от ориентации
контура в данной точке пространства.
Ориентация контура задаётся вектором
![]() нормали к плоскости контура и направление
нормали к плоскости контура и направление
![]() связано с
направлением обхода по контуру правилом
правого винта.
связано с
направлением обхода по контуру правилом
правого винта.
Полученный предел
представляет собой скалярную величину,
которая ведёт себя как проекция некоторого
вектора на направление нормали
![]() к плоскости контура, по которому берётся
циркуляция. Этот вектор называют ротором
(вихрем) поля
к плоскости контура, по которому берётся
циркуляция. Этот вектор называют ротором
(вихрем) поля
![]() и обозначают символом rot
и обозначают символом rot![]() ,
т. е.
,
т. е.
![]() (17)
(17)
где справа стоит
проекция вектора rot![]() на нормаль
на нормаль
![]() .
Значит, в каждой точке векторного поля
.
Значит, в каждой точке векторного поля
![]() имеется вектор rot
имеется вектор rot![]() ,
направление и модуль которого связаны
со свойствами самого поля в данной
точке. Направление вектора rot
,
направление и модуль которого связаны
со свойствами самого поля в данной
точке. Направление вектора rot![]() определяется тем направлением нормали
определяется тем направлением нормали
![]() площади S,
при котором достигается максимальное
значение величины (17), являющейся
одновременно модулем вектора rot
площади S,
при котором достигается максимальное
значение величины (17), являющейся
одновременно модулем вектора rot![]() .
Формально rot
.
Формально rot![]() можно рассматривать как векторное
произведение оператора
(Набла) на вектор
можно рассматривать как векторное
произведение оператора
(Набла) на вектор
![]() ,
т. е.
,
т. е.
![]() .
.
ЗАМЕЧАНИЕ:
-
скалярное произведение векторов обозначается:
![]() ;
;
![]() ;
;
-
векторное произведение векторов обозначается:
![]() ;
;
![]() ;
;
![]() .
.
Произведение
![]() в координатном представлении записывается
с помощью определителя:
в координатном представлении записывается
с помощью определителя:
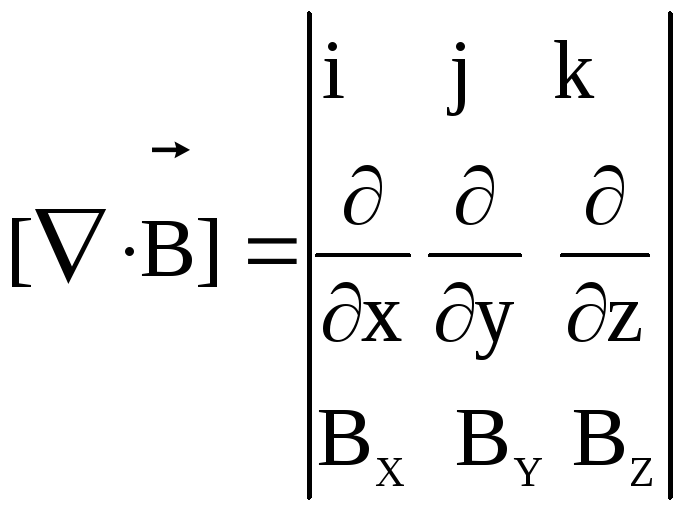 , (18)
, (18)
где
![]() – орты осей декартовых координат. Это
выражение справедливо и для любого
другого векторного поля, в частности
вектора
– орты осей декартовых координат. Это
выражение справедливо и для любого
другого векторного поля, в частности
вектора
![]() .
.
В соответствии с (17) уравнение (5) можно представить в виде:
![]() или
или
![]() ,
,
отсюда:
![]() (19)
(19)
Это и есть
дифференциальная
форма теоремы о циркуляции вектора
![]() .
.
Ротор поля
![]() совпадает с направлением вектора
совпадает с направлением вектора
![]() .
.
В электростатическом поле:
![]() . (20)
. (20)
Циркуляция вектора
![]() равна нулю,
поэтому
равна нулю,
поэтому
![]() ,
т. е. векторное поле
,
т. е. векторное поле
![]() является соленоидальным.
является соленоидальным.
ЗАКЛЮЧЕНИЕ!!!
ТЕОРЕМА ГАУССА:
В интегральной форме
![]() ,
,
в дифференциальной форме
div
![]() = 0 или
= 0 или
![]() .
.
Эта теорема выражает
тот факт, что силовые линии магнитного
поля замкнуты, поэтому число линий
вектора
![]() ,
выходящих из любого объема, всегда равно
числу линий, входящих в этот объем.
,
выходящих из любого объема, всегда равно
числу линий, входящих в этот объем.
Записанная в дифференциальной форме теорема Гаусса показывает, что в природе не существует магнитных зарядов, аналогичных электрическим зарядам, локализованным в пространстве. Магнитное поле порождают не магнитные заряды, а электрические токи.
ТЕОРЕМА О ЦИРКУЛЯЦИИ:
В интегральной форме
![]() ,
,
в дифференциальной форме
![]() или
или
![]()
Тот факт, что
циркуляция вектора
![]() означает, что поле вектора
означает, что поле вектора
![]() не потенциально
(в отличие
от поля
не потенциально
(в отличие
от поля
![]() ).
Такое поле называют вихревым
или соленоидальным.
).
Такое поле называют вихревым
или соленоидальным.
