Закон ома для неоднородного участка цепи.

Неоднородным называют участок цепи, на котором действуют сторонние силы (имеется источник ЭДС).

Пусть электрический ток течёт вдоль тонких проводов. В этом случае направление тока будет совпадать с направлением оси провода, и плотность тока будет одинакова во всех точках сечения проводника. При этом площадь сечения провода может быть неодинаковой по длине проводника.

Разделим уравнение (15) на , полученное выражение умножим скалярно на элемент оси провода dl, взятый по направлению от сечения 1 к сечению 2 (его мы примем за положительное направление) и затем проинтегрируем по длине провода от сечения 1 к сечению 2:

. (16)

Преобразуем подынтегральное выражение у первого интеграла: заменим  на 1/ и на j_ldl, где j_l  проекция вектора на направление векторa . Учтём, что j_l – величина алгебраическая, зависит от направления и ; если  то j_l> 0, при   j_l < 0. Заменим j_l на I/S , где I  сила тока величина тоже алгебраическая. Для постоянного тока во всех сечениях цепи I = const, тогда её выносим за знак интеграла:

.

Выражение  это сопротивление цепи участка длиной dl, а интеграл от этого выражения  полное сопротивление R участка цепи между сечениями 1 и 2.

В правой части (16) первый интеграл  это разность потенциалов φ₁  φ₂, а второй интеграл представляет собой ЭДС  электродвижущую силу ε, действующую на данном участке цепи:

ε₁₂ =. (17)

Как и сила тока, ЭДС является алгебраической величиной.

С учетом этих замечаний из выражения (16) получим:

IR = ₁  ₂ + ₁₂. (18)

Это уравнение выражает интегральную форму закона Ома, для неоднородного участка цепи в отличие от дифференциальной формы (15).

ЧАСТНЫЕ СЛУЧАИ:

Для замкнутой цепи φ₁ = φ₂ и следовательно (18) приобретает вид:

RI = ε, (19)

где R  полное сопротивление замкнутой цепи; ε  алгебраическая сумма отдельных ЭДС в данной цепи.

Для участка цепи содержащий сам источник ЭДС между его клеммами 1 и 2 в выражении (18) R  внутреннее сопротивление источника, а φ₁  φ₂ – разность потенциалов на его клеммах. Если источник разомкнут, то I = 0 и:

 = φ₂  φ₁, (20)

т.е. ЭДС источника можно определить как разность потенциалов на его клеммах в разомкнутом состоянии. Очевидно, что φ₂  φ₁ – разность потенциалов источника замкнутого на внешнее сопротивление всегда меньше его ЭДС.

Дополнительно (Савельев: новый §26 стр. 102-103; старый §35)

Разветвлённые цепи. Правило кирхгофа.

Обобщенный закон Ома:

,

позволяет рассчитать любую сложную цепь. Однако, проще это сделать с помощью правил Кирхгофа.

Разветвлённые цепи  это цепи, содержащие несколько замкнутых контуров. Узлом называется любая точка разветвления цепи, в которой сходится не менее трех проводников. Ток, «входящий» в узел, считают положительным, «выходящий»  отрицательным.

Р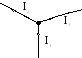асчет разветвленных цепей, например расчёт токов в отдельных её ветвях разветвлённой цепи проводят используя правила Кирхгофа:

1. Алгебраическая сумма токов, сходящихся в узле, равна нулю:

или I₁  I₂ + I₃ = 0.

2. В любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил токов I_i на сопротивления R_i, соответствующих участков контура, равна алгебраической сумме ЭДС, встречающихся в этом контуре:

Дополнительно (Савельев: новый §27,см. примеры; старый §36)