
kornil / Новые Изменения мои Part2 / с083_090
.doc__________________________________________Тема 5. Примеры___
|
|
Здесь требуется найти производную функции, заданной параметрически. |
|
|
|
Если
записать производную в дифференциальном
виде:
|
|
|
|
После сокращения на dt получаем производную. |
|
|
|
Надо найти производную неявно заданной функции. |
|
|
Продифференцируем обе части равенства, учитывая, что переменная у является функцией переменной х. |
|
|
Сделаем алгебраические преобразования, направленные на выделение производной в полученном выражении. |
|
|
Из
последнего равенства найдем
|
|
|
Найти дифференциал функции при данном значении х. |
|
|
|
Дифференциал
функции вычисляется по формуле :
|
|
|
|
Подставим
в полученное выражение заданное
значение
|
|
|
|
Окончательно:
|
|
Задание 2. Найти пределы, используя правило Лопиталя.
ПРИМЕРЫ
а) Раскрытие неопределенных
выражений вида
![]() .
.
|
|
Определим
вид неопределенного выражения. Правило
Лопиталя можно применять при
неопределенностях вида
|
||
|
|
После вычисления производных неопределенное выражение сохранилось. |
||
|
= |
Применим правило еще раз. Неопределенность раскрыта, получен ответ. |
||
|
|
Приведение к общему знаменателю позволяет получить неопределенное выражение, которое можно раскрывать с помощью правила Лопиталя. |
||
|
|
Перед
вычислением производных учтем, что
|
||
|
Здесь вместо повторного применения правила Лопиталя произведена замена эквивалентными бесконечно малыми величинами. |
|||
б) Раскрытие степенных неопределенностей.
|
|
В данном случае надо раскрыть степенную неопределенность. Степень числа е вычисляется как предел с |
|
|
|
неопределенным выражением, раскрывающемся по правилу Лопиталя. |
|
|
|
Правило применяется дважды, а затем, вместо того, чтобы применять его третий раз, можно выделить глав- |
|
|
=
|
ные части числителя и знаменателя. После сокращения получим значение числа А. |
|
|
|
Подставляем число А в степень числа е и получаем ответ. |
|
|
|
Степенная неопределенность. Степень числа е вычисляется как предел произведения функций и |
||
|
|
всегда можно воспользоваться эквивалентными бесконечно малыми величинами и произвести замену |
||
|
|
при
|
||
|
|
Чтобы применить правило Лопиталя, приводим выражение под знаком предела к дроби. |
||
|
= |
После сокращения получен ответ. |
||
|
|
Число А надо подставить в степень числа е и найти предел. |
||
Задание 3. Методами дифференциального исчисления исследовать функцию и построить ее график.
ПРИМЕР
Задана
функция
![]() .
Требуется исследовать её свойства и
построить график.
.
Требуется исследовать её свойства и
построить график.
Разобьем процесс исследования функции на три этапа:
-
На первом этапе рассмотрим аналитическое выражение, задающее функцию:
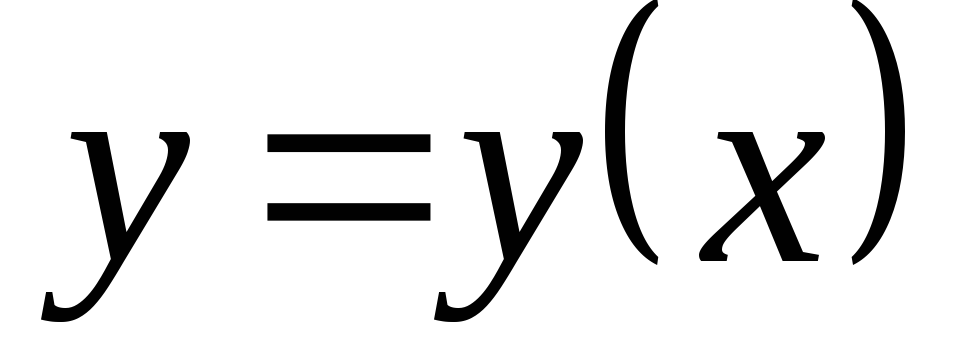 и определим следующие характеристики.
и определим следующие характеристики.
|
1 |
Областьдопустимых значений (D(x), ОДЗ) |
Знаменатель
функции обращается в нуль в точке
х = 1.
ОДЗ данной функции
|
|
2 |
Нули функции и точки пересечения с осью 0У |
График
пересечет ось ординат ОУ
при значении
абсциссы х
= 0,
|
|
3 |
Четная, нечетная, общего вида |
|
|
4 |
Исследование точек разрыва и поведения функции на границах ОДЗ |
Исследуем вид разрыва в точке х=1.
В точке х=1 имеется разрыв 2-го рода и прямая х=1 является вертикальной асимптотой функции. |
|
5 |
Наклонные и горизонтальные асимптоты функции |
|
-
На втором этапе найдем первую производную функции и по ее аналитическому выражению определим следующие характеристики самой функции.
|
1 |
Точки возможных экстремумов - критические точки |
|
|
|
Интервалы возрастания / убывания (монотонности). Обозначения: − возрастает, − убывает |
Критическая точка и точка разрыва разделяют интервалы монотонности функции. Определим знаки первой производной на каждом интервале.
|
|
3 |
Экстремумы (max / min) |
Теперь
можно сделать заключение об экстремуме
функции в точке х=0.
При переходе через эту точку первая
производная меняет знак, убывание
функции сменяет возрастание, поэтому
это точка минимума функции :
В точке х = 1 не существует экстремума, т.к. это точка разрыва второго рода. |
-
На третьем этапе найдем вторую производную функции и по ее аналитическому выражению определим следующие характеристики самой функции.
|
1 |
Точки возможного перегиба графика функции |
Найдем
точки возможного перегиба графика
функции:
|
|
|
Интервалы выпуклости / вогнутости. Обозначения: − вогнута, − выпукла |
Две найденные точки разделяют интервалы выпуклости / вогнутости функции. Определим знаки второй производной на каждом интервале.
|
|
3 |
Точки перегиба |
Теперь
можно сделать заключение о точке
перегиба функции. При переходе через
точку х =
-1/2 вторая
производная меняет знак, выпуклость
функции меняется на вогнутость, поэтому
это точка перегиба функции :
|
П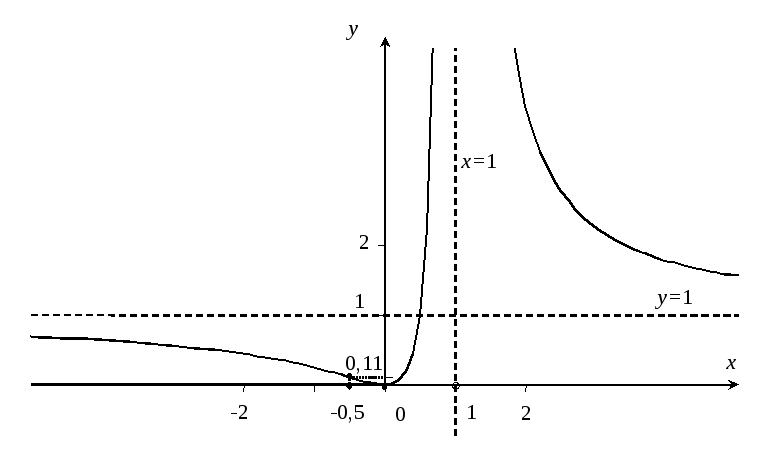 остроение
графика функции рекомендуется начинать
с построения всех
асимптот и всех точек, через которые
проходит график функции, которые получены
в процессе исследования.
остроение
графика функции рекомендуется начинать
с построения всех
асимптот и всех точек, через которые
проходит график функции, которые получены
в процессе исследования.
Задание 4. Задана функция полных издержек производства С(х) и зависимость между удельной ценой р и количеством единиц продукции х, которую можно продавать по этой цене: р = р(х). При каком объеме производства х0 прибыль будет максимальной и какова ее величина ?
ПРИМЕР
Предприятие
производит х
единиц продукции по цене
![]() а издержки производства задаются
функцией
а издержки производства задаются
функцией
![]()
Найти оптимальный для предприятия объем выпуска продукции и соответствующую ему максимальную прибыль.
Пусть TR(x) – валовой доход, z(x) – прибыль от реализации х единиц продукции по цене р(х).
Тогда
![]()
![]()
где р(х), C(х) – заданные функции.
Для решения задачи следует исследовать функцию z(x) на экстремум. При этом прибыль будет максимальна для такого объема выпуска продукции, для которого
![]()
Формируем
z(x),
находим
![]() и, решив уравнение
и, решив уравнение
![]() получаем критическую точку.
получаем критическую точку.
![]()
![]()
![]()
![]() -
критическая точка.
-
критическая точка.
Находим
![]() и определяем ее знак при х=150:
и определяем ее знак при х=150:
![]()
Значит, х=150 – точка максимума функции z(x), т.е. оптимальный объем производства составляет 150 единиц продукции.
Определяем максимальную прибыль производства, т.е. zmax = z(150).
При
х=150
цена
![]() валовой доход
валовой доход
TR(150) = 35×150 = 5250.
Издержки производства
![]()
максимальная прибыль Zmax = 5250 – 3350 = 1900.
Замечания.
-
Не следует ожидать, что при решении подобных задач будут получаться только целые числа. Подразумевается, что объем выпуска продукции х исчисляется в денежном выражении и может быть не целым.
-
Если для определения х0 получено квадратное уравнение, то отрицательный корень отбрасывают, как не удовлетворяющий экономическому смыслу задачи.

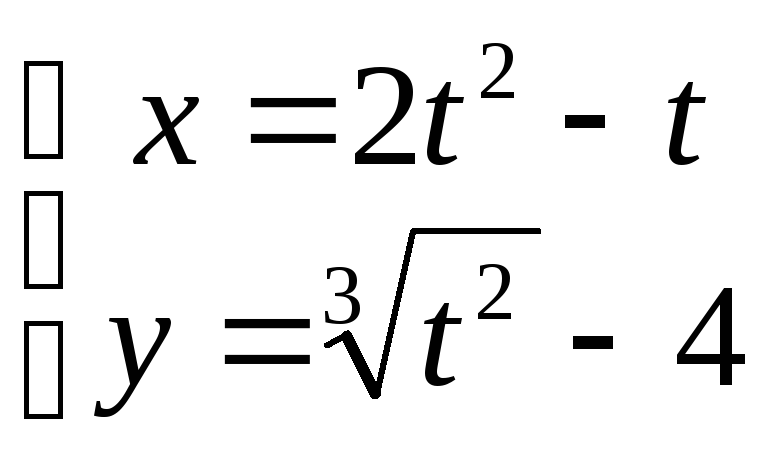
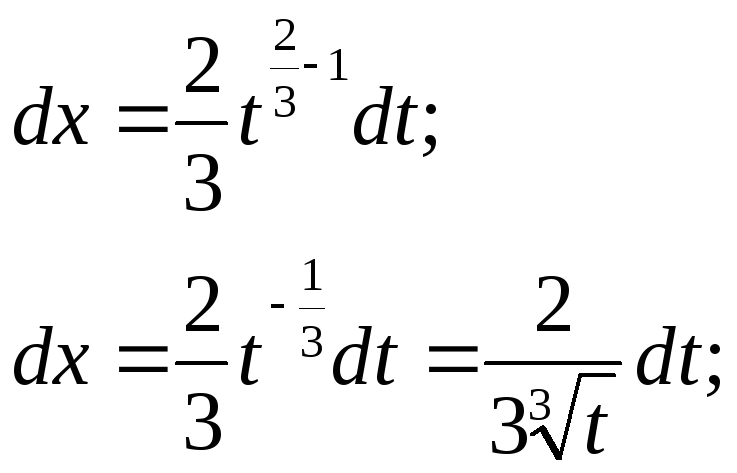
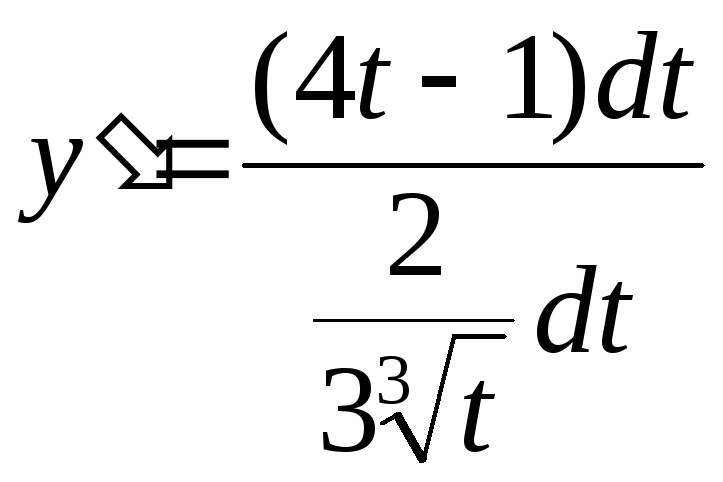 =
=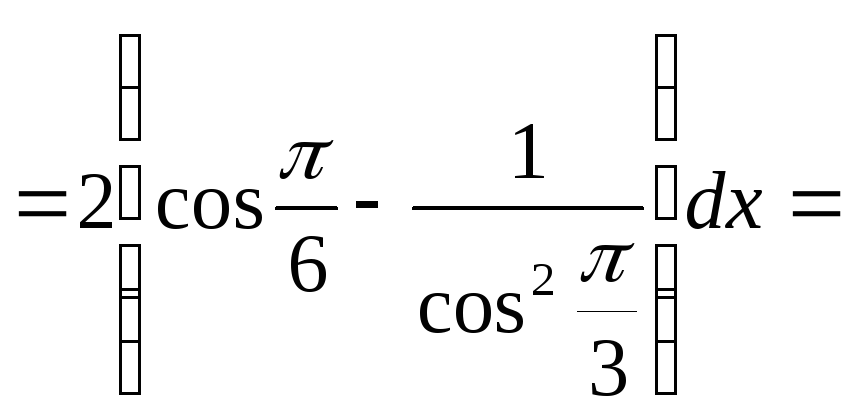
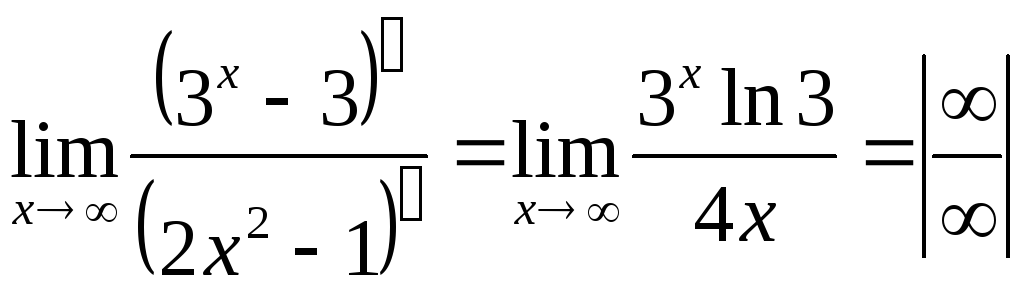
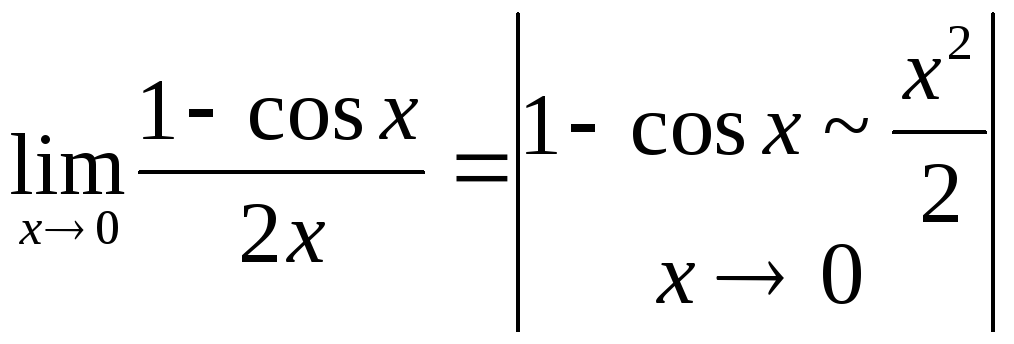 =
=
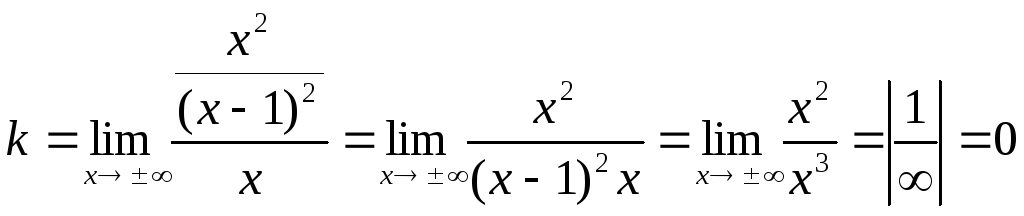 ;
;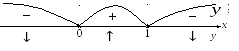 2
2 2
2