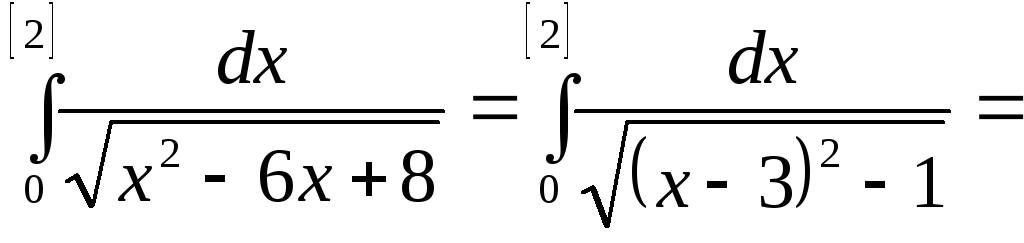kornil / Новые Изменения мои Part2 / c137_144
.doc__________________________________________Тема 7. Примеры___
|
28. |
а)
б) |
29. |
а)
б) |
30. |
а)
б) |
Примеры выполнения обязательных заданий по теме 7
Задание 1. Вычислить определенные интегралы.
ПРИМЕРЫ
|
|
Представим заданный интеграл в виде суммы интегралов. |
|||
|
= |
Вносим
под знак дифференциала в первом
во
втором
|
|||
|
= |
Находим первообразные (см. таблицу в теме 6), подставляем в них пределы по формуле Ньютона-Лейбница. |
|||
|
= = |
Учитываем,
что
|
|||
|
|
Заметим, что в числителе |
|||
|
= |
подынтегральной функции стоит производная знаменателя и внесем ее под знак дифференциала. Получаем
степенной интеграл,
По
формуле Ньютона-Лейбница подставляем
пределы интегрирования, причем
|
|||
|
= |
Окончательный ответ. |
|||
=
=
,
.
=
=
.
,
=
=
.
,
.
.
|
|
Подобные интегралы вычисляются методом замены переменной, а именно - рекомендуемой |
||
|
|
тригонометрической подстановкой (см. тему 6, таблица рекомендуемых тригонометрических подстановок). - обязательно изменить пределы интегрирования. |
||
|
= |
Производим упрощение полученных выражений. |
||
|
= |
Вычисляем интеграл за счет тригонометрических преобразований. |
||
|
= |
Подставляем пределы,
|
||
=
;
.
=
=
.
,
.
Задание 2. Вычислить площади фигур, ограниченных указанными линиями. Сделать чертеж области, площадь которой вычисляется.
ПРИМЕР
|
|
Построим заданную область, ограниченную заданными линиями на плоскости Х0У. |
||
|
|
При
при
В
общем вид линии
|
||
|
Всеми тремя заданными линиями ограничена заштрихованная область. Составляем формулу для вычисления площади: |
|||
|
|
Каждый интеграл вычислим по отдельности. |
||
|
|
Площадь
прямоугольника под прямой
|
||
|
|
Вычисление интеграла методом по частям. |
||
|
=
=
|
Упрощаем первообразную и подставляем пределы интегрирования.
|
||
,
− крайние точки.
подобен
виду линии
.
;
.
=
=
-
Если бы область
была задана линиями :
,
то следовало бы вычислять
.
Задание 3. Задачи с экономическим содержанием.
ПРИМЕРЫ
Найти среднее значение издержек производства (AC), выраженное в денежных единицах, если задана функция издержек С(q) и пределы изменения объема выпускаемой продукции q от q1 до q2. Указать объем продукции (qc), при котором издержки принимают среднее значение.
|
Пусть С(q)=3q2+4q+1, объем продукции q меняется от 0 до 3 единиц. |
|||
|
|
Согласно теореме о среднем значении. |
||
|
|
В
нашем случае
|
||
|
|
т.е. среднее значение издержек АС = 16. |
||
|
|
Определим, при каком объеме продукции издержки принимают это значение. |
||
|
|
Учитывая, что объем продукции не может быть отрицательным, берем только |
||
|
т.е.
|
положительный корень уравнения. |
||
(ден.
ед.)
единиц продукции.Ответ. Среднее значение издержек производства 16 ден.ед., причем оно достигается при выпуске продукции в 1,67 ед.
- Выпуск продукции может быть как целым, так и дробным числом, т.к. не указано, что это за продукция и в каких единицах измеряется.
Определить объем продукции, произведенной рабочим за n-й час рабочего дня (например, n=2 означает время работы от t=1 до t=2), если производительность труда f(t) задана. Определить среднюю производительность труда за 8-ми часовую смену и указать час, в который эта производительность достигается.
Пусть
.
|
|
Найдем объем продукции, произведенной рабочим за четвертый час рабочего дня. |
|||
|
=
(все приближенные значения округляем до двух знаков после запятой) |
При
вычислении первообразной разбиваем
интеграл на сумму двух интегралов и
в первом вносим под знак дифференциала:
|
|||
|
|
Средняя производительность труда за рабочую смену – по |
|||
|
|
теореме о среднем (см. пример 1 в 3-м задании), округляем до двух знаков после запятой. |
|||
|
|
Найдем час, в который достигается средняя производительность труда. |
|||
|
|
После приведения к общему знаменателю и приведения подобных получаем решение уравнения |
|||
;
ед.
.
;
(ден.ед.)
;
;
,
Ответ.
Объем продукции, произведенной за
четвертый час рабочей смены – около
3,14 ед. Средняя производительность труда
– около 3,16 ед. продукции, она достигается
на третьем часу рабочей смены (
час.).
Пусть
производительность труда в течение
смены меняется следующим образом:
.
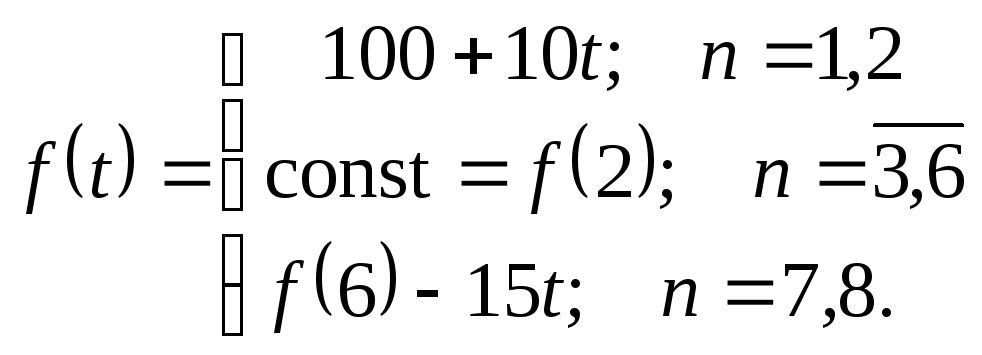Найти объем продукции, произведенной
за первые три часа рабочего дня и среднюю
производительность.
|
|
Расшифруем заданную кусочно-непрерывную функцию производительности труда. |
|||
|
|
Найдем объем продукции, произведенной за первые три часа рабочего дня. |
|||
|
|
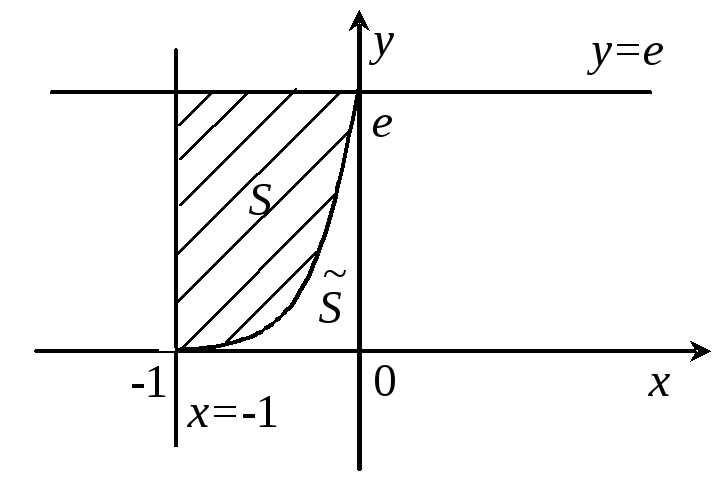
Для контроля построим график производительности труда. |
|||
|
В данном случае
вычисление интеграла поддается
элементарной геометрической проверке
– надо найти площадь под графиком
функции при
|
||||
|
|
Объем продукции, выпущенной за смену.
|
|||
|
|
Средняя производительность труда по теореме о среднем. |
|||
|
Час, в который достигается средняя производительность труда, можно приблизительно определить по графику, проведя прямую линию |
||||
|
Ответ. Объем продукции, произведенной за первые три часа рабочей смены – 340 ед. Средняя производительность труда – 91,25 ед. продукции, нет такого часа, на котором работа идет со средней производительностью. |
||||
- первые два часа
смены;
-
с третьего по шестой час;
-
последние два часа.
.
Она складывается из суммы площадей
прямоугольной трапеции
и прямоугольника
(проверьте самостоятельно).
.
.
В данной задаче она не пересекает
графика функции производительности
труда, поэтому нет такого часа за всю
смену, в который производительность
труда – средняя.
|
Определить дисконтированный доход А ден. ед. за k лет, если базовые капиталовложения А0 ден. ед., ежегодные дополнительные вложения равны А1 ден. ед., годовая процентная ставка q%. Проценты начисляются непрерывно. |
Определение начальной суммы по ее конечной величине, полученной через время t (лет) при годовом проценте (процентной ставке) q, называется дисконтированием (см. тему 4). Задачи такого рода встречаются при определении экономической эффективности капитальных вложений.
Пусть Аt – конечная сумма, полученная за t лет, и А – дисконтируемая (начальная) сумма, которую в финансовом анализе называют также современной суммой. Если проценты простые, то At = A (1 + r t), где r = q/100 – удельная процентная ставка. Тогда A = A t/ (1 + r t). В случае сложных процентов At = A (1+r t)t и потому A = At / (1 + r t)t.
Пусть поступающий ежегодно доход изменяется во времени и описывается функцией f(t) и при удельной норме процента, равной r, процент начисляется непрерывно. Можно показать, что в этом случае дисконтированный доход A за время Т вычисляется по формуле
Определим дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 млрд.ден.ед., и намечается ежегодно увеличивать капиталовложения на 1 млрд.ден.ед.
|
|
Очевидно, что
капиталовложения задаются функцией,
зависящей от года
|
|
|
Дисконтированная сумма капиталовложений. Интеграл вычисляется методом по частям: |
|
|
Проделайте вычисления самостоятельно и убедитесь, что А = 30,5 млрд. ден. ед. |
|
Ответ. Для получения одинаковой наращенной суммы через три года ежегодные капиталовложения от 10 до 13 млрд.ден.ед. равносильны одновременным первоначальным вложениям 30,5 млрд.ден.ед. при той же, начисляемой непрерывно, процентной ставке. |
|
.
Задание 4. Исследовать несобственные интегралы на сходимость по признаку сравнения и вычислить.
ПРИМЕРЫ
|
|
Несобственный интеграл 1-го рода. Для
вычисления вносим под знак дифференциала:
|
||||
|
= |
По определению НИ-1. |
||||
|
= |
Учитывая, что
|
||||
|
|
Исследуем интеграл на сходимость по
признаку сравнения. Определим функцию,
эквивалентную подынтегральной при
|
||||
|
Применялось выделение главной части в бесконечно больших величинах. Сравниваем со специальной функцией для НИ-1. |
|||||
|
|
НИ-1 сходится |
||||
=
.
=
и
получаем в пределе число (const). Значит,
этот НИ-1 сходится.
.
;
|
|
Несобственный интеграл 2-го рода.
Подынтегральная функция имеет разрыв
в точке
|
||||
|
обращается в ноль. Для вычисления
выделяем полный квадрат:
|
|||||
|
= |
По определению НИ-2. |
||||
|
|
Подставляем пределы интегрирования и вычисляем предел. |
||||
|
|
Получаем в пределе число (const). Значит, НИ-2 сходится. |
||||
|
По другому можно исследовать интеграл на сходимость по признаку сравнения.
Определим
функцию, эквивалентную подынтегральной
при
|
|||||
|
|
Найдем корни и разложим квадратный трехчлен по корням. |
||||
|
|
Применялось правило, позволяющее заменять сомножители, не стремящиеся к нулю соответствующими числами. |
||||
|
|
Сравниваем со специальной функцией для НИ-2, имеющих разрыв подынтегральной функции на верхнем пределе. НИ-2 сходится. |
||||
,
в ней знаменатель
и учитываем, что
.
.
.
;
.
- Обратите внимание! Выделение полного квадрата может привести к различным табличным интегралам. Также часто встречается ошибка, когда не учитывается знак минус:
Знак минус нельзя выносить из-под квадратного корня!
Сравним два интеграла с одинаковыми подынтегральными функциями, но различными пределами.
|
НИ-1 |
НИ-2 |
Для вычисления интегралы разбиваются на сумму интегралов. |
|
|
|
|
||
|
= |
= |
||
|
НИ-1 расходится,
потому что
|
НИ-2 расходится,
потому что
|
|
|
|
Исследование на сходимость по признаку сходимости.
|
|||
|
|
|
Обратите внимание, на то, что при исследовании сравнение происходит с одинаковыми функциями, но смысл разный. |
|
|
|
т.к. точка разрыва
|
||
,
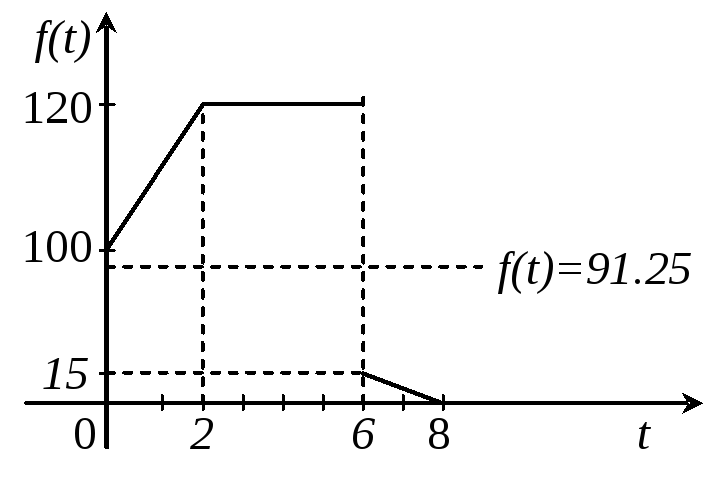
а остальные пределы конечны.
,
а остальные пределы конечны.
;
НИ-1 расходится.
;
;
НИ-2 расходится.