Непрерывность функции. Классификация разрывов функции

 Функция у = у(х) называется непрерывной в т. х = х₀, если она определена в этой точке и некоторой ее окрестности, и предел функции при х  х₀ совпадает с ее значением в т. х = х₀, т.е.

Выполнение этого равенства предполагает выполнение следующих условий:

• Функция определена в точкеи некоторой ее окрестности.

• Существует конечный правый предел функции

.

• Существует конечный левый предел функции

.

• Односторонние пределы равны, то есть b₁ = b₂ , и их общее значение есть предел функции в точке .

• Предел функции равен значению функции в точк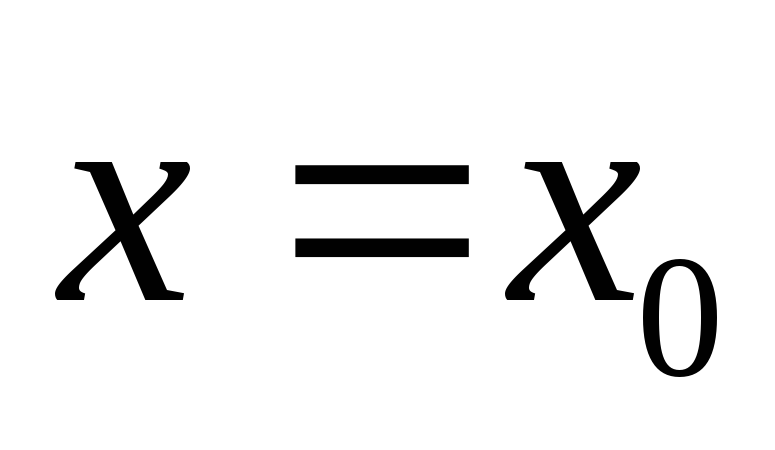е , т.е.

.

Если не выполняется хотя бы одно из перечисленных условий, то говорят, что функция имеет (терпит) разрыв непрерывности в точке . Исходя из особенностей поведения функции до точек разрыва неопределенности справа и слева, выделяются точки разрыва I и II рода.

 Для определения типа точек разрыва непрерывности следует:

1. Найти точки, в которых функция может иметь разрыв. Это либо точки, не принадлежащие области допустимых значений аргумента функции, либо точки, в которых меняется аналитическое выражение функции.

2. В каждой такой точке проанализировать односторонние пределы, которые могут либо существовать:

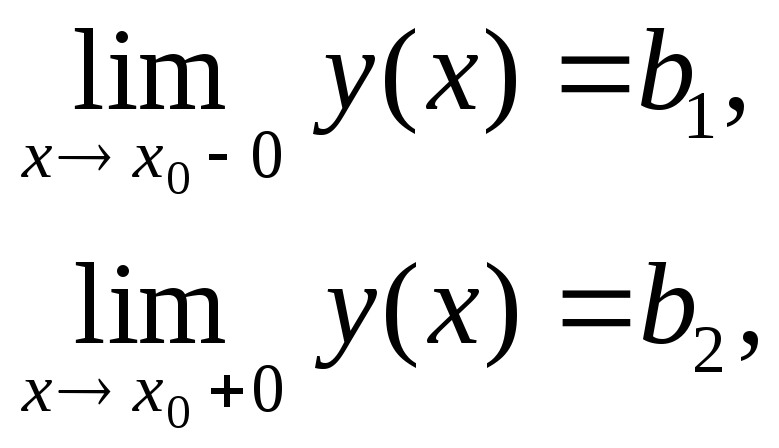
либо стремиться к бесконечности

либо быть неопределенными.

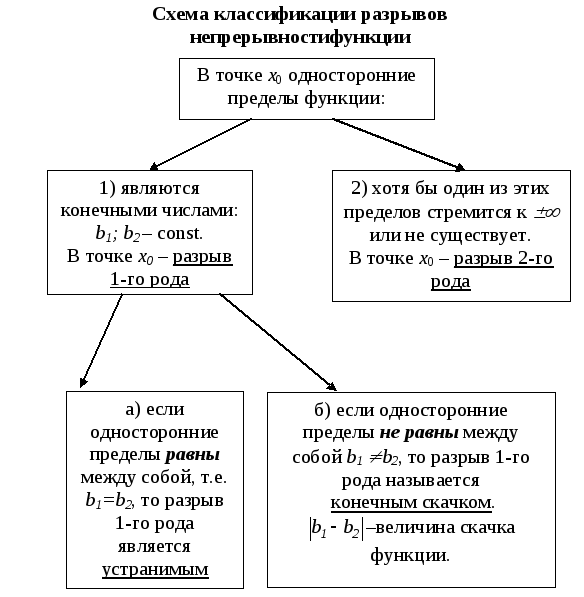
3) Учитывая полученные значения односторонних пределов, сделать вывод о характере разрыва непрерывности функции, пользуясь схемой.

 Вопреки распространенному мнению, в практических задачах прерывность функции встречается не менее часто, чем непрерывность.

Рассмотрение функции как прерывной или непрерывной зависит от конкретных условий. В связи с большей простотой решения многих вопросов для непрерывной функции иногда допускают, что функция непрерывна.

Однако, нередко функция, строго говоря, имеющая много разрывов, может с известным приближением рассматриваться как непрерывная, причем в ее анализе могут применяться соответствующие приемы.

Например, численность населения страны как функция времени носит, строго говоря, такой же прерывный характер, как и мощность доменного производства. Она увеличивается или уменьшается на единицу в моменты соответственно рождения или смерти какого-либо гражданина. Но изменение численности на 1 настолько мало ее меняет в масштабах страны с населением в несколько десятков миллионов, что функцию можно считать непрерывной.

Но стоит перейти от численности населения страны к численности населения дома или квартиры, то въезд или выезд одного жителя будут настолько заметно ее менять, что эту функцию нельзя практически рассматривать как непрерывную.

Рассмотрим мощность черной металлургии по производству чугуна, как функцию времени (рис.2). Очевидно, изменение этой мощности, измеряемой числом м³ полезного объема доменных печей, происходит в моменты окончания строительства и сдачи в эксплуатацию каждой новой печи или в моменты остановки и закрытия старых печей. В эти моменты функция мощности имеет разрыв 1–го рода – скачки, а в промежутках между ними остается постоянной.