Основные правила вычисления пределов, связанные с арифметическими операциями

Если функции y = f(x)иy = (x)имеют конечные пределы прих  а, то:

1.  , предел суммы равен сумме пределов.

2.  , предел произведения равен произведению пределов.

3.  , предел частного равен отношению пределов, если.

4.  , предел постоянной величины равен самой постоянной.

5.  − постоянную величину можно выносить за знак предела.

Первый и второй замечательные пределы и следствия из них.

Таблица эквивалентных БМ величин

ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ:	.
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ:	, , где …(натуральное число)

Второй замечательный предел на практике можно использовать и в такой форме ( а, в – соnst)

Следствия из замечательных пределов – это соотношения эквивалентности между некоторыми БМ величинами.

ТАБЛИЦА ЭКВИВАЛЕНТНЫХ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН

Пусть , т.е. является бесконечно малой величиной.

Следствия из первого замечательного предела.	Следствия из второго замечательного предела.
sin x ~ x tg x ~ x arcsin x ~ x arctg x ~ x 1 - cos x ~ x2 / 2

Техника вычисления пределов

При вычислении пределов функций используется правило предельного перехода под знаком непрерывной функции,которое формулируется так:

.

Оно справедливо для всех элементарных функций, так как они непрерывны в своих областях определения. Из правила следует, что при вычислении пределов, прежде всего, необходимо аргумент функции заменить его предельным значением и выяснить, имеется ли неопределенноесоотношениие. Кнеопределеннымотносятся соотношения вида:

, .

Если такое выражение существует, необходимо выполнить тождественные преобразования, в результате которых устраняется неопределенность, а затем вычисляется предел.

Логическая схема техники вычисления пределов

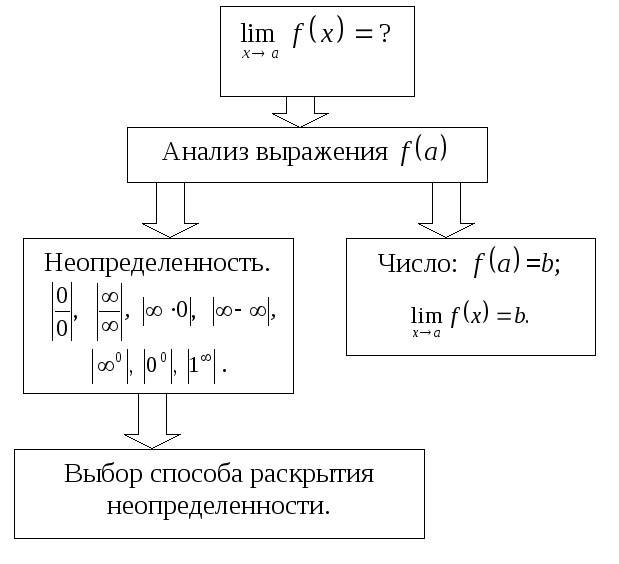
Основные этапы поиска способа раскрытия неопределенности представлены в алгоритме на следующей странице, а конкретные примеры вычисления пределов функции приведены в разделе "Примеры выполнения обязательных заданий по теме 4".

Общий алгоритм вычисления предела функции

.



Подставить (в том числе и) в.

Проанализировать полученное неопределенное соотношение: .

			Если это отношение многочленов, то выделяется главная часть:
	 		алгебраические преобразования : выделение в числителе и знаменателе множителя, стремящегося к нулю.		Если это отношение многочленов, то определяются корни числителя и знаменателя дроби и многочлены раскладываются на множители.
					Если предел содержит квадратные (кубические) корни, то следует умножить и разделить дробь на соответствующий сопряженный множитель.
			использование эквивалентных бесконечно малых величин.		Отношение степенных функций.
			Это неопределенное выражение приводится к виду: или .
		 	Если , то привести к общему знаменателю и получить.
			Преобразование иррациональности .
			Приведение предела к виду второго замечательного предела, т.е. , где- бесконечно малая величина. Затем используют известные формулы или .