9.3 Производные и дифференциалы высших порядков

Частные производные функции u= (х₁, х₂, ... , х_n): (i=) в свою очередь являются функциями n переменныхх₁, х₂, ... , х_n и могут иметь частные производные по этим переменным.

Частная производная от по переменнойх_i, т.е. выражение называется частной производной 2-го порядка и обозначается. Еслиk i, частную производную называют смешанной. Аналогично определяют частные производные 3-го, 4-го и т.д. порядков.

Теорема Шварца. Если функция u= (х₁, х₂, ... , х_n) имеет в некоторой области D всевозможные частные производные до m-го порядка включительно, причем все они непрерывны в этой области, то значение любой ее смешанной производной m-го порядка не зависит от того порядка, в котором производятся последовательные дифференцирования.

Пусть функция u= (х₁, х₂, ... , х_n) имеет в области D непрерывные частные производные 1-го порядка. Тогда, как известно, ее полный дифференциал du находится по формуле (9.2.1). Очевидно, du также является функцией n переменных х₁, х₂, ... , х_n и можно говорить о полном дифференциале от этого дифференциала d(du), который называется дифференциалом 2-го порядка и обозначается d²u. Аналогично можно определить d³u=d(d²u) - дифференциал 3-го порядка и т.д.

Таким образом, dⁿu=d(d^n-1u) называется дифференциалом n-го порядка.

При этом приращения dх₁, dх₂, ... , dх_n независимых переменных рассматриваются как постоянные и при переходе от одного дифференциала к другому остаются одними и теми же.

Например, для функции двух переменных z=f(x,y)

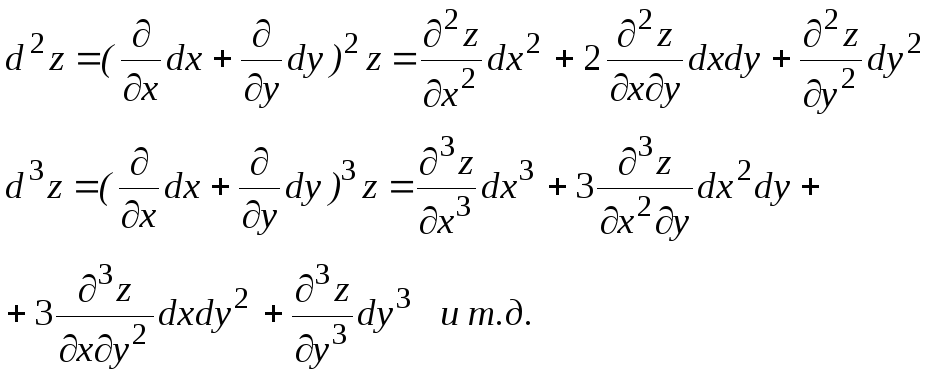(9.4.1)

Для дифференциалов высших порядков имеет место символическая формула

(9.4.2)

Пример 1. u= e ^xyz. Найти .

. .

.

Пример 2. Показать, что

что и требовалось доказать.

9.4 Экстремум функции многих переменных. Условный экстремум

1. Исследование функции многих переменных на локальный (безусловный) экстремум

Исследование функции на локальный экстремум включает в себя следующие основные этапы:

1) нахождение области определения функции;

2) нахождение точек возможного экстремума (критических точек);

3) проверка достаточных условий экстремума.

Для нахождения точек возможного экстремума нужно найти все частные производные 1-го порядка данной функции и приравнять их к нулю. Решая полученную систему уравнений, находят стационарные точки функции. Если есть точки, в которых частные производные не существуют, их тоже присоединяют к точкам возможного экстремума.

На третьем этапе исследований, если функция дважды дифференцируема в некоторой окрестности стационарной точки M₀ и все частные производные 2-го порядка непрерывны в ней, то вычисляем их значения в этой точке. Если в этой точке второй дифференциал является знакоопределенной квадратичной формой дифференциаловdx₁, dx₂, ... , dx_n , то в этой точке функция (M) принимает экстремальное значение, причем если d²(M₀)< 0, то в точке M₀ функция принимает локальный максимум, если d² (M₀)>0, то локальный минимум.

Сформулируем критерий знакоопределенности квадратичной формы - критерий Сильвестра: для того, чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы выполнялись неравенства:

.

Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы выполнялись неравенства:

.

Случай функции двух переменных. Пусть в некоторой окрестности стационарной точки M₀(x_o, y_o) функция (x, y) дважды дифференцируемая и все частные производные второго порядка

непрерывны в этой точке. Тогда, если  (M₀) = a₁₁ a₂₂ - a₁₂² > 0, то функция

(x, y) имеет в этой точке локальный экстремум, а именно: максимум при a₁₁ < 0 и минимум при a₁₁ > 0. Если же  (M₀) = a₂₁ a₂₂ - a₁₂² < 0, то функция (x, y) не имеет локального экстремума в этой точке. Случай, когда  (M₀)=0, требует дополнительных исследований.

Случай функции n (n>2) переменных. Пусть в некоторой окрестности точки M₀(х₁^о, х₂^о, ... , х_n^о ) функция (M)= (х₁, х₂, ... , х_n) m раз дифференцируемая и все частные производные m-го порядка непрерывны в этой точке, к тому же

d(M₀)=0, d² ( M₀) = d³ (M₀) =... = d^m-1 (M₀)= 0, d^m (M₀) > или < 0.

Тогда, если m - нечетное, то точка M₀ не будет точкой экстремума; если же m - четное, то в точке M₀ функция (x, y) имеет экстремум: локальный максимум, если d^m (M₀) < 0 и локальный минимум, если d^m (M₀) > 0.

Пример 1. Исследовать на экстремум функцию . По необходимому условию существования экстремума найдем стационарные точки

или

, откуда получаем четыре стационарные точки: . В каждой из точек проверим выполнение достаточного условия, т.е. проверим знак второго дифференциала.

1) В точке :

. Экстремума нет.

2) В точке :

в точке М₂ минимум и ;

3) В точке

Экстремума нет.

4) В точке

в точке М₄ максимум и

Решение задач удобно оформлять в виде таблицы

точки	М1(1;2)	М2(2;1)	М3(-1;-2)	М4(-2;-1)
	6	12	-6	-12
	12	6	-12	-6
	6	12	-6	-12
	>0	>0	<0	<0
	<0	>0	<0	>0
extr	нет	min	нет	max
Z		-28		28

Пример 2. Исследовать на локальный экстремум функцию

u=x²+ y²+ z²+ 2x+4y- 6z.

Из системы u_x= 2x +2=0; u_y= 2y +4=0; u_z= 2z - 6= 0 находим единственную стационарную точку: x=-1, y=-2, z=3. Найдем вторые производные:

Отсюда

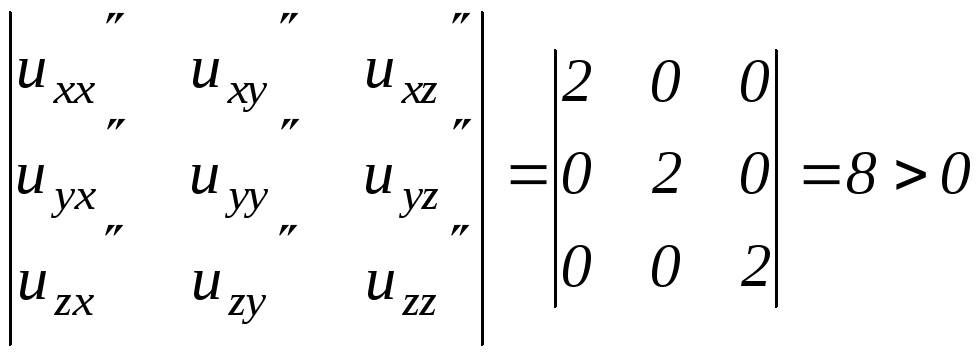
Итак, второй дифференциал, согласно критерию Сильвестра, есть знакоположительная квадратичная форма. Поэтому в точке М₀(-1,-2,3) функция имеет минимум (u _min = -14).

Пример 3. Исследовать на экстремум функцию: .

1) Функция определена для всех x є R и y є R.

2) z_x = z_y =.

Легко удостовериться, что эта функция не имеет стационарных точек. Но в точке М₀(0,0) частные производные первого порядка не существуют, так как разностные отношения

не имеют предела. Поэтому, точка М₀(0, 0) является точкой возможного экстремума. Из того, что приращение z(x,y)-z(0,0) =отрицательно, делаем вывод, что в этой точке функция имеет максимум, причем z_max =1.