
- •Глава 9. Функции многих переменных
- •9.1 Основные понятия
- •9.2 Частные производные и полный дифференциал
- •9.3 Производные и дифференциалы высших порядков
- •9.4 Экстремум функции многих переменных. Условный экстремум
- •Исследование функции многих переменных на локальный (безусловный) экстремум
- •9.4.2 Исследование функции многих переменных на условный экстремум
- •9.5 Функции нескольких переменных в экономической теории
- •9.6 Метод наименьших квадратов
Глава 9. Функции многих переменных
В настоящей главе мы будем рассматривать обобщение понятий и методов дифференциального исчисления на случай функции двух, трех и более независимых переменных.
9.1 Основные понятия
Переменная величина u называется функцией независимых переменных х1, х2, ... , хn , если каждой совокупности значений (х1, х2, ... , хn) этих переменных из данной области их изменения по некоторому правилу или закону поставлено в соответствие одно или несколько значений величины u. Обозначение: u= (х1, х2, ... , хn) или u= u(х1, х2, ... , хn). В случае функции трех переменных пишут u=f(x,y,z), а в случае функции двух переменных - u=f(x,y) или z= f(x, y), z= z(x, y).
Совокупность n чисел х1, х2, ... , хn называют “точкой” в области изменения переменных х1, х2, ... , хn и говорят о значении функции u в этой точке. Если функция задана аналитическим выражением (формулой) без каких-либо дополнительных условий, то под ее областью определения понимают область существования ее аналитического выражения, т.е. совокупность всех тех точек, в которых данное аналитическое выражение определено и принимает только действительные и конечные значения.
Область определения функции трех переменных представляет собой некоторую пространственную область, в частности, некоторый объем. Область определения функции двух переменных представляет собой плоскую область.
Пример 1. Найти область определения функции z= ln (4+4x-y2).
Логарифм определен только при положительных значениях его аргумента, поэтому 4+ 4x- y2 > 0 или 4+ 4x > y2. Никаких других ограничений на аргументы x и y не дано.
Ч тобы
изобразить геометрически область D,
найдем сначала ее границу 4+4x
= y2 или
y2
= 4(x +
1).
тобы
изобразить геометрически область D,
найдем сначала ее границу 4+4x
= y2 или
y2
= 4(x +
1).
Полученное уравнение определяет параболу (рис. 9.1). Парабола делит всю плоскость на две части - внутреннюю и внешнюю по отношению к параболе. Для точек одной из ее частей выполняется неравенство y2 < 4 + 4x, а для другой y2 > 4 + 4x ( на самой параболе y2 = 4 + 4x).
Рис. 9.1
Чтобы установить, какая из этих двух частей является областью определения данной функции, т.е. удовлетворяет условию y2<4+4x, достаточно проверить это условие для какой-нибудь одной точки, не лежащей на параболе. Например, начало координат О(0, 0) лежит внутри параболы и удовлетворяет нужному условию 0< 4+4 0. Следовательно, рассматриваемая область D состоит из точек внутри параболы. Т. к. сама парабола в область D не входит, границу области - параболу- на рисунке отметим пунктиром.
9.2 Частные производные и полный дифференциал
Пусть
функция u=
(х1,
х2,
... , хn)
определена в некоторой области D и точка
M0(х1о,
х2о,
... , хnо
) - внутренняя точка этой области. Если
существует предел (конечный или
бесконечный) отношения частного
приращения ![]() =f(х1о,
... , хkо+xk,
... , хnо)
- f(х1о,
... , хnо)
функции u
в точке M0 к
соответствующему приращению переменной
xk
при xk0
, то этот предел называется частной
производной функции
u=
(х1,
х2,
... , хn)
в точке M0
по переменной xk
и обозначается
=f(х1о,
... , хkо+xk,
... , хnо)
- f(х1о,
... , хnо)
функции u
в точке M0 к
соответствующему приращению переменной
xk
при xk0
, то этот предел называется частной
производной функции
u=
(х1,
х2,
... , хn)
в точке M0
по переменной xk
и обозначается
![]()
Таким
образом,
![]()
Частные
производные находятся по обычным
правилам и формулам дифференцирования.
При этом, находя
![]() ,
все переменные, кромеxk,
рассматриваем как постоянные.
,
все переменные, кромеxk,
рассматриваем как постоянные.
Функция u= (х1, х2, ... , хn) называется дифференцируемой в точке M0, если ее полное приращение
u= f(х1о+x1, ... , х2о+x2, ... , хnо+xn) - f(х1о, ... , хnо)
представимо в этой точке в виде
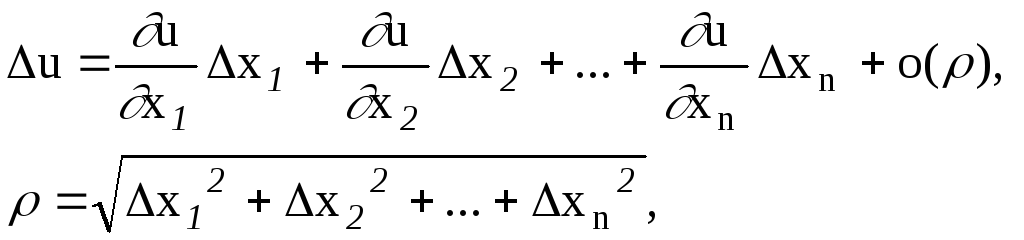 где
где
а все частные производные вычислены в точке M0.
Полным дифференциалом функции u в точке M0 называется главная часть ее полного приращения в этой точке, линейная относительно приращений x1, x2, ..., xn.
Следовательно,
![]()
Т.к.
дифференциалы независимых переменных
совпадают с их приращениями, т.е. xk=
dxk
(k=![]() ),
полный дифференциал можно переписать
в виде
),
полный дифференциал можно переписать
в виде
![]()
При
достаточно малых приращениях независимых
переменных, т.е. при малом
![]() можно
полное приращение функции приближенно
заменить ее полным дифференциалом:
можно
полное приращение функции приближенно
заменить ее полным дифференциалом:
u du (9.2.2)
или
f(х1о+x1, ... , хnо+xn) f(х1о, ... , хnо)+ df(х1о, ... , хnо) (9.2.3)
Эту формулу применяют для приближенных вычислений приращений функции или приближенных значений функций в какой-то точке.
Пример
1.
Найти полный дифференциал функции
![]()
Находим частные производные
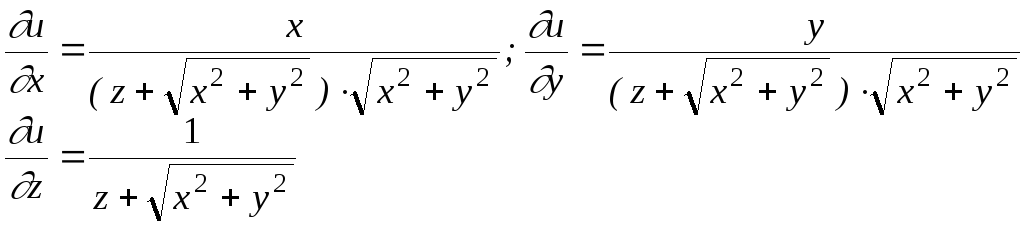
По формуле (9.2.1) получаем
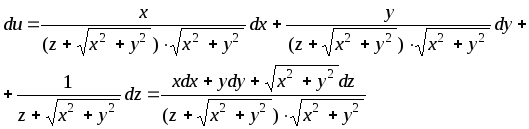
Пример 2. Вычислить приближенно (0,98)3,03 .
Искомое число можно рассматривать как значение функции z=x y при x=х0+x, y=y0+y, где х0=1, y0=3, x =-0,02, y = 0,03.
z(1,
3)=13
= 1;
![]()
По формуле (9.2.3) имеем 0,983,03 1+3(-0,02)=0,94.
