4. Линейные неоднородные дифференциальные уравнения второго порядка.Метод вариации произвольных постоянных

Рассмотрим линейное неоднородное дифференциальное уравнение 2-го порядка:

(ЛНДУ). (10.4.1)

Соответствующее ему линейное однородное дифференциальное уравнение 2-го порядка:

(ЛОДУ). (10.4.2)

По теореме о структуре общего решения ЛНДУ общее решение дифференциального уравнения (10.4.1) имеет вид:

,

где и-линейно независимые частные решения дифференциального уравнения (10.4.2), а- какое-нибудь частное решение дифференциального уравнения (10.4.1);- произвольные постоянные.

Для отыскания общего решения ЛНДУ (10.4.1) рассмотрим метод вариации произвольных постоянных (в форме Лагранжа).

1. Находим общее решение ЛОДУ (10.4.2)

, (10.4.3)

где и-линейно независимые частные решения дифференциального уравнения (10.4.2),- произвольные постоянные.

2. Запишем общее решение ЛНДУ (10.4.1) в форме (10.4.3)

, (10.4.4)

где и-неизвестные функции. Функциииподберем так, чтобы функция, определяемая соотношением (10.4.4) была решением дифференциального уравнения (10.4.1).

3. Для определения инеобходимо решить систему линейных неоднородных алгебраических уравнений:

. (10.4.5)

Из системы уравнений (10.4.5)иопределяются единственным образом, так как определитель системы

,

функции илинейно независимы.

Пусть и. Тогдаи, гдеипостоянные интегрирования.

4. Найденные иподставим в соотношение (10.4.4) и получим общее решение ЛНДУ(10.4.1).

или

. (10.4.6)

В соотношении (10.4.6)- общее решение ЛОДУ (10.4.2), а функция-частное решение ЛНДУ(10.4.1).

Пример. Найти общее решение ЛНДУ: (10.4.7)

1. Найдем общее решение ЛОДУ: ;

, отсюдаи - общее решение однородного дифференциального уравнения.

2. Общее решение ЛНДУ ищем в виде , (10.4.8)

где и- неизвестные функции, подлежащие определению.

3. Для определения этих функций составим систему уравнений:

,

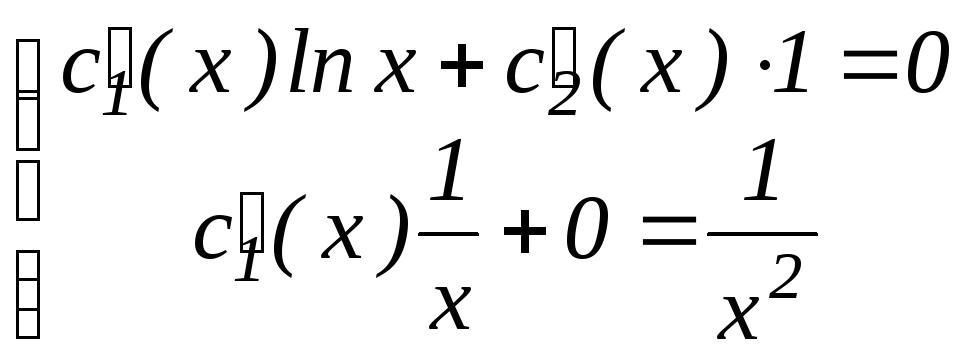отсюда находим ,. Интегрируя,получим:

4. Подставив ив соотношение (10.4.8), получим общее решение ЛНДУ (10.4.7): или

,

где - общее решение ЛОДУ, - частное решение ЛНДУ.

Примечание. Метод вариации произвольных постоянных применим к ЛНДУ более высоких порядков (n>2).

10.5 Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами и с правой частью специального вида. Метод неопределенных коэффициентов

Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами:

, (10.5.1)

где - действительные числа. Соответствующее ему ЛОДУ:

.

Известно, что общее решение ЛОДУ имеет вид:

,

где - произвольные постоянные, а- фундаментальная система решений этого дифференциального уравнения.

Общее решение ЛНДУ (10.5.1) определяется формулой:

,

где - какое-нибудь частное решение (10.5.1).

В предыдущем параграфе был рассмотрен общий метод отыскания общего решения ЛНДУ – метод вариации произвольных постоянных.

Если имеетспециальный вид, то частное решениеможет быть найденометодом неопределенных коэффициентов.

1.Пусть правая часть дифференциального уравнения имеет вид: , где- многочлен степени n,- какое-нибудь действительное число.

1.1. Еслине является корнем характеристического уравнения, то частное решение ищем в виде: , где- многочлен степениn с неопределенными коэффициентами.

Чтобы найти эти коэффициенты, подставим функцию в дифференциальное уравнение и в полученном тождестве приравняем коэффициенты слева и справа при одинаковых степенях . Получим системуn+1уравнения для определения коэффициентов.

Пример 1. Найти общее решение ЛНДУ: ,.

Рассмотрим соответствующее ЛОДУ: .

Характеристическое уравнение , корни этого уравнения. Таким образом, числоне является корнем характеристического уравнения.

Частное решение ЛНДУ ищем в виде: .

Подставим функцию и ее производнуюв данное дифференциальное уравнение и получим тождество:

Приравнивая коэффициенты при одинаковых степенях , получим систему:

. Отсюда,, тогда

.

Общее решение дифференциального уравнения:

.

1.2.Если является действительным корнем характеристического уравнения кратностиk, то частное решение ищем в виде: .

Пример 2.Найти общее решение ЛНДУ:

, .

Рассмотрим соответствующее ЛОДУ:

Характеристическое уравнение ,, корни уравнения. Таким образом, числоявляется действительным корнем 2-й кратности характеристического уравнения.

Частное решение ищем в виде: .

Подставим функцию и ее производныеив данное дифференциальное уравнение и получим тождество: .

.

Тогда . Общее решение дифференциального уравнения:

2. Пусть правая часть дифференциального уравнения имеет вид:

,

где - многочлены, и- какие-нибудь действительные числа.Заметим, что многочленыимогут иметь нулевую степень.

2.1. Числоне является корнем характеристического уравнения, тогда частное решение ищем в виде: ,

где и- многочлены с неопределенными коэффициентами, степень которых равна наивысшей из степеней многочленови.

Пример 3. Найти общее решение ЛНДУ

.

Рассмотрим соответствующее ЛОДУ:

,.

Число не является корнем характеристического уравнения.

Частное решение ищем в виде: .

Подставим функцию и ее производныеив данное дифференциальное уравнение и получим тождество:

приравнивая коэффициенты при и, получим систему :

или.

Отсюда . Тогда. Общее решение дифференциального уравнения: .

2.2.Числоявляется корнем характеристического уравнения кратностиk, то частное решение ищем в виде: .

Пример 4. Найти общее решение ЛНДУ:

, .

Рассмотрим соответствующее ЛОДУ:

.

Число является корнем характеристического уравнения. Частное решение ищется в виде .

Подставим функцию и ее производныеив данное дифференциальное уравнение и получим тождество

.



Тогда .Общее решение дифференциального уравнения: .

Примечание. Если ЛНДУ имеет вид: , то частное решениеэтого уравнения можно представить в виде суммы, гдеисоответствующие частные решения уравнений: ;

Пример 5. Найти общее решение ЛНДУ: ,

.

Рассмотрим соответствующее ЛОДУ: .

Характеристическое уравнение корни

Частное решение ЛНДУ ищем в виде , гдеисоответственно частные решения дифференциальных уравнений

, .

Частные решения этих дифференциальных уравнений соответственно равны

Частное решение ЛНДУ:

Общее решение ЛНДУ :