2. Уравнение Бернулли

.

Уравнение Бернулли сводится к линейному уравнению с помощью замены переменной. Разделим все уравнение на : и сделаем замену переменной . Тогда. Подставим в уравнение: или. Получили неоднородное линейное уравнение для функцииz. После его решения можно найти.

Пример. или.

Перейдем к линейному уравнению, учитывая, что и. . Здесь.

Пусть z=UV;

• . Удобно принятьС=1,тогда .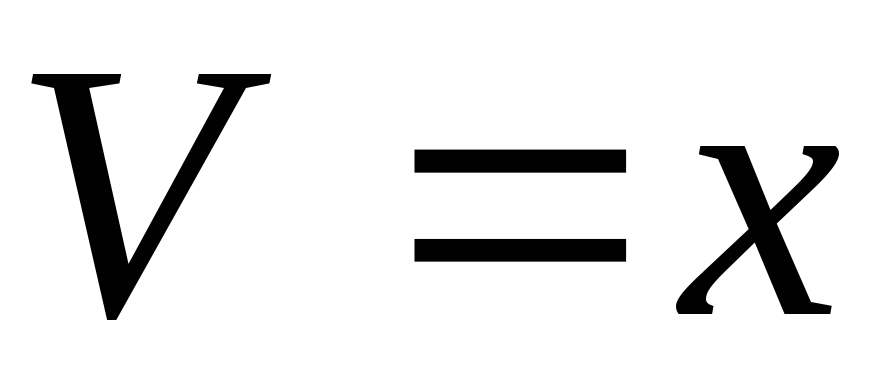

• 

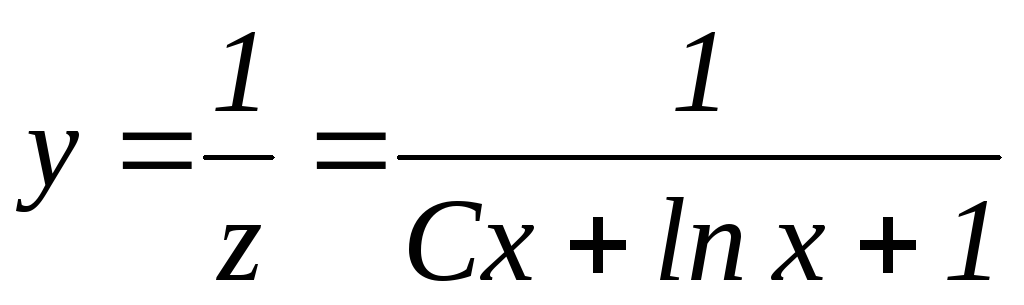• , . Уравнение имеет еще решениеy=0.

2. Уравнения, допускающие понижение порядка

Рассмотрим частные типы уравнений второго порядка.

• 1.Уравнение не содержит явно искомой функции:. Понижение порядка такого уравнения достигается введением новой функции,. И уравнение принимает вид. Это уже уравнениеIпорядка.

• 2.Уравнение не содержит явно независимой переменной:. В этом случае за новую функцию принимают, а за новую независимую переменную. Тогда. Такая замена переменных приведет к дифференциальному уравнению первого порядка:.

Пример 1.. Уравнение не содержит искомой функции. Поэтому,,. Это линейное дифференциальное уравнениеIпорядка. Его можно решить так:

.

Заменяя на, снова приходим к уравнениюIпорядка ,

откуда находим .

Пример 2.. Уравнение не содержит явно.

Замена .

а) .. Это уравнение с разделяющимися переменными.

.

Заменяя наснова приходим к уравнению первого порядка .

Разделяя переменные и интегрируя, найдем общее решение уравнения:

.

б) , но это решение содержится в общем (при).

3. Линейные однородные дифференциальные уравнения

Дифференциальные уравнения вида

, (10.3.1)

где некоторые функции, называются однородными линейными дифференциальными уравнениямиn-го порядка (ЛОДУ).

Фундаментальной системой решений уравнения (10.3.1), называют любые nлинейно независимых решений.

Пусть решения дифференциального уравненияn-го порядка. Определитель называется определителемВронского.

Если W(x) решенийтождественно равен нулю, то эти решения линейно зависимы. ЕслиW(x) не обращается в нуль ни в одной точке, то это означает, что решения линейно независимы и составляютфундаментальную систему решений. Любое однородное линейное уравнение имеет фундаментальную систему решений.

Если фундаментальная система решений однородного линейного уравнения, то его общее решение представимо в виде:

,

где произвольные постоянные.

10.3.1 Решение лоду с постоянными коэффициентами

Так какивходят в уравнение линейно, будем искать решение в виде, где-действительное или комплексное число (все производные этой функции отличаются от нее только постоянным множителем:).

Подставив в уравнение, получим:.

Так как , а коэффициенты, то нахождение фундаментальной системы решений уравнения (10.3.1) сводится к алгебраическим операциям, а именно к решению алгебраического уравненияn-ой степени:

.

Это уравнение называется характеристическим уравнением дифференциального уравнения.

Характеристическое уравнение, как алгебраическое уравнение n-ой степени имеетn корней (вещественных или комплексных).

При решении характеристического уравнения возможны случаи:

• 1.Корни характеристического уравнения- действительные и различные, тогда дифференциальное уравнение (10.3.1) имеетn линейно независимых частных решений

.

Общее решение дифференциального уравнения (10.3.1) имеет вид

Пример 1. Найти общее решение ЛОДУ

,

-характеристическое уравнение.

Корни характеристического уравнения -действительные и разные. Тогда линейно независимые частные решения дифференциального уравнения имеют вид:

общее решение дифференциального уравнения есть

• 2.Корни характеристического уравнения действительные, но среди них есть кратные. Пусть, то есть-действительный корень кратностиk, остальные корни характеристического уравнения- действительные и различные. Тогда действительному корнюкратностиkотвечаетk частных линейно независимых решений дифференциального уравнения (10.3.1):

.

Общее решение дифференциального уравнения (10.3.1) имеет вид:

.

Пример 2. Найти общее решение ЛОДУ:

или-характеристическое уравнение

Корни характеристического уравнения - действительные числа. Действительный кореньявляется корнем 3-й кратности. Этому корню отвечают 3 линейно независимых частных решения дифференциального уравнения вида:.

Остальным корням характеристического уравнения отвечают линейно независимые частные решения вида:.

Общее решение дифференциального уравнения :

.

• 3.Среди корней характеристического уравнения кроме действительных, есть и комплексно-сопряженные, но нет кратных. Пусть.

Этим комплексно-сопряженным корням отвечают два частных линейно независимых решения дифференциального уравнения:

Общее решение дифференциального уравнения (10.3.1) имеет вид:

.

Пример 3. Найти общее решение ЛОДУ:

- характеристическое уравнение.

; ;

Корни характеристического уравнения:

Паре комплексно-сопряженных корней характеристического уравнения соответствуют два частных линейно независимых решения:

.

Действительным корням характеристического уравнения соответствуют два частных линейно независимых решения: .

Общее решение дифференциального уравнения:

.

• 4.Среди корней характеристического уравнения есть кратные комплексно-сопряженные корни. Пустьи- пара комплексно-сопряженных корней характеристического уравнения кратностиk. Тогда паре комплексно-сопряженных корней характеристического уравнения кратностиk отвечает2kлинейно независимых частных решений дифференциального уравнения: , остальным корням характеристического уравнения отвечаютn-2kчастных линейно независимых решений вида: .

Общее решение дифференциального уравнения (10.3.1) имеет вид:

.

Пример 4. Найти общее решение дифференциального уравнения:

характеристическое уравнение, .

Корни характеристического уравнения икомплексно-сопряженные 2-й кратности. Частные линейно независимые решения дифференциального уравнения:

.

Общее решение дифференциального уравнения:

.