Глава 10. Дифференциальные уравнения

Дифференциальным уравнением называется уравнение, связывающее неизвестную функцию, ее производные и независимые переменные.

Если функция, входящая в уравнение, зависит от одной независимой переменной, то уравнение называется обыкновенным дифференциальным уравнением. Порядок старшей производной, входящей в данное уравнение, называетсяпорядкомуравнения. Обыкновенное дифференциальное уравнение n-го порядка имеет вид:

Всякая функция , удовлетворяющая дифференциальному уравнению, т.е. обращающая его в тождество, называетсярешениемэтого уравнения. Выражениенеявно задающее решение уравнения, называетсяинтеграломэтого уравнения. График решения дифференциального уравнения называется егоинтегральной кривой. Процесс отыскания решения дифференциального уравнения называется его интегрированием.

10.1 Дифференциальные уравнения I порядка, разрешенные относительно производной

Общий вид дифференциального уравнения I порядка:

(10.1.1)

Предположим, что уравнение (10.1.1) можно разрешить относительно производной. Тогда оно примет вид:

(10.1.2)

Задача, в которой требуется найти решение уравнения , удовлетворяющее начальному условию, называетсязадачей Коши.

Решение, удовлетворяющее начальному условию, называется частным решениемдифференциального уравнения.

Теоремасуществования и единственности решения задачи Коши:

Если правая часть уравненияи ее частная производная поуопределены и непрерывны в областиDизмененияx и y,то какова бы ни была внутренняя точкаэтой области, данное уравнение имеет единственное решение, принимающее призаданное значение.

Геометрически это означает, что через каждую точку области проходит (и притом только одна) интегральная кривая.

Общим решениемдифференциального уравнения I порядка называется функция, зависящая от одной произвольной постояннойС и удовлетворяющая двум условиям:

1. функция 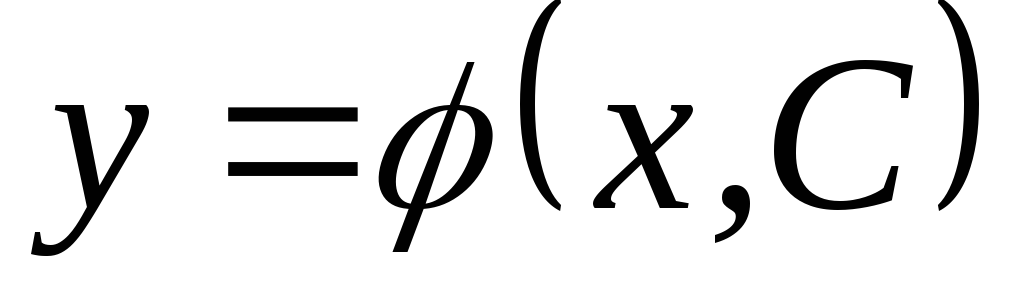является решением уравнения при любых допустимых значениях постояннойС;

2. выбором произвольной постоянной С можно удовлетворить любому начальному условию.

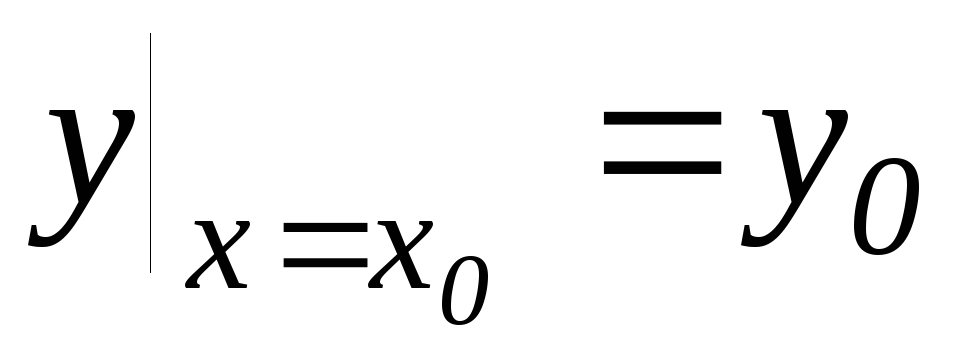Соотношение , определяющее общее решение в неявном виде, называетсяобщим интеграломуравнения и представляет собой однопараметрическое семейство интегральных кривых.

Частным решениемдифференциального уравнения (10.1.1) называется решение, получаемое из общего решения при каком-либо определенном значении произвольной постояннойС. Решение задачи Коши, т. е. решение, удовлетворяющее начальным условиям, является частным решением.

Рассмотрим методы интегрирования дифференциального уравнения (10.1.2) для частных случаев правой части.

10.1.1 Уравнения с разделяющимися переменными

Дифференциальное уравнение (10.1.2) называется уравнением с разделяющимися переменными, если его правая часть может быть представлена как произведение двух функций, каждая из которых зависит только от одной переменной:.

Тогда уравнение (10.1.2) можно переписать в виде: . (10.1.3)

Разделим обе части уравнения на

В последнем уравнении переменные разделены. Считая, что есть решение уравнения, получим тождество. Интегрируя его, найдем общий интеграл уравнения

.

Если существуют значения, при которых функцияобращается в нульто уравнение (10.1.3) будет иметь еще и решения

Пример.. Это уравнение с разделяющимися переменными.

Предполагая, что , разделим переменные:. После интег-

рирования получим:

.

Откуда (общее решение уравнения). Решениесодержится в общем при.

К уравнениям с разделяющимися переменными с помощью замены переменных приводятся и уравнения вида: . Сделаем замену переменной, приняв в качестве новой функции функцию. Тогда. Учитывая, что, получим. Это уравнение с разделяющимися переменными. Разделяя переменные и интегрируя, найдем

.

Пример. . Правая часть этого уравнения есть функция от. Поэтому полагая получим: . Разделяем переменные и интегрируем. Так как, то общий интеграл уравнения имеет вид: .