2. Однородные дифференциальные уравнения

Дифференциальное уравнение (10.1.2) называется однородным, если - является однородной функцией нулевой степени. Функция- называется однородной функциейтой степени, если выполняется тождество .

Например, однородная функция с показателем однородности, так как .

Функция однородная 3-ей степени, функция- однородная нулевой степени.

Если функция является однородной нулевой степени, то она удовлетворяет тождеству и ее всегда можно представить, как функцию отношения. Действительно, положив в тождестве, получим . Левая часть полученного равенства зависит только от. Уравнение (10.1.2) принимает вид: .

С помощью замены переменной это уравнение сводится к уравнению с разделяющимися переменными: . Подставив эти выражения в уравнение, найдем.

Разделяя переменные и интегрируя, получим общий интеграл уравнения

.

При разделении переменных мы делим на , предполагая, что это выражение отлично от нуля. Если же существует такое значение, при котором, то мы имеем еще решениеили.

Пример. . Это однородное дифференциальное уравнение, т.к.- однородная функция нулевой степени. Для его решения вводим новую функцию. В новых переменных уравнение имеет вид:

.

После интегрирования найдем: или . Подставляя значение, получим общий интеграл уравнения . Кроме того, решением является.

Уравнения вида: приводятся к однородному дифференциальному уравнению с помощью замены переменной. Следует заметить, что если быибыли равны нулю, то уравнение было бы однородным (в этом можно было бы убедиться, разделив числитель и знаменатель на). Уравненияиопределяют две прямые. Для уничтожения в уравнениях прямых свободных членов, надо перенести начало координат в точку пересечения этих прямых. Решая систему уравнений: найдем точку пересечения прямых

.

Замена переменных приводит к уравнению

. Это однородное дифференциальное уравнение.

Изложенный метод нельзя применять, если прямые параллельны. Но в этом случае коэффициенты при текущих координатах пропорциональны и дифференциальное уравнение может быть записано в виде:

.

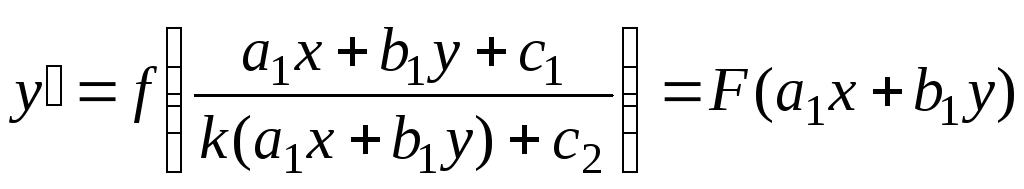Следовательно, замена переменных преобразует уравнение в уравнение с разделяющимися переменными.

Пример. . Решая систему уравнений, найдем.

Полагая ,, будем иметь или.

Замена переменных z=/или=zприводит к уравнению с разделяющимися переменными. .

Разделяем переменные: . Интегрируем .

Подставляя , получим. Возвращаясь к старым переменным, найдем общий интеграл дифференциального уравнения

.

2. Линейные дифференциальные уравнения

Дифференциальное уравнение называется линейным, еслиивходят в него линейно, т.е. впервой степени:. Т.к., то уравнение приводится к виду:

(10.1.4)

где - правая часть линейного дифференциального уравнения.

Если , то уравнение называетсяоднороднымлинейным уравнением. Если, то имеемнеоднородноелинейное уравнение.

Рассмотрим один из возможных способов решения уравнения (10.1.4), способ Бернулли-Фурье. Будем искать решение в виде y=U(x)V(x). Таким образом, искомыми становятся функцииU(x)иV(x).

Подставим y=UVив (10.1.4), тогда

Найдем функцию V(x)как частное решение уравнения с разделяющимися переменными:. После интегрирования получим:, где постояннуюСможно задать произвольно.

Тогда функция U(x)также может быть найдена как решение уравнения с разделяющимися переменными.

Можно получить и общую формулу для решения линейного дифференциального уравнения 1-го порядка :

.

Пример. или.

Здесь .

Найдем;;

. ПустьС=1, тогда частное решение.

Теперь найдем U(x):;;.

Решение исходного уравнения : или