
baldin_kv_red_matematika_dlia_gumanitariev
.pdf
Приведем конкретный пример вычисления определенного интеграла по формуле (5.20)
Пример 5.35.
Используя метод трапеции приближенно вычислим интег-
рал , приняв n = 10. Этот интеграл, как и интеграл пре-
дыдущего примера, является неберущимся. В данном случае
.
Теперь по формуле (5.20) получаем
в) Формула парабол (формула симпсона).
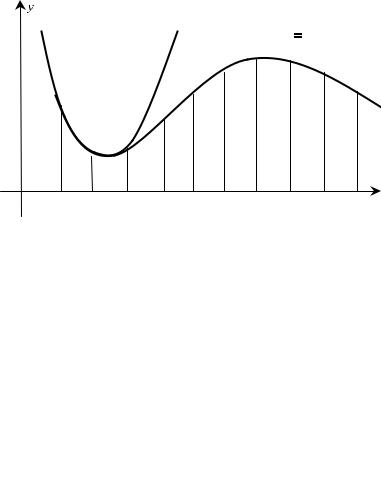
Пусть на отрезке [a, b] задана непрерывная функция y = f(x). Разделим [a, b] на четное число частей n = 2m. Сущность способа заключается в том, что отрезки прямых, ограничивающих элементарные трапеции сверху, заменяют дугами парабол, оси которых параллельны оси 0у (см. рис. 5.21).
Уравнения таких парабол имеет вид y = cx2 + dx + p. Коэффициенты c, d, p можно однозначно найти по трем точкам, если абсциссы их различны. Дуги парабол проводят через каждую тройку точек. Криволинейную трапецию aABb заменяют суммой площадей криволинейных трапеций, ограниченных дугами парабол. Площадь первой из таких параболических трапеций равна
191
|
|
y f(xy) |
|
A |
B |
|
|
|
|
A1 |
|
|
|
A2 |
|
|
x |
0 |
a =x0 x1 x2 |
xn= b |
Рис. 5.21
площадь второй равна:  и т. д. Искомая формула Симпсона имеет вид [1, 16]:
и т. д. Искомая формула Симпсона имеет вид [1, 16]:
(5.21)
Формула оценки погрешности, получающейся при приближенном вычислении интеграла, в этом случае имеет вид [9]:
где 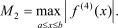
Применение формулы (5.21) значительно повышает точность вычисления определенного интеграла. Метод прямоугольников является наиболее простым и наименее точным способом. Выбор способа приближенного интегрирования зависит от подынтегральной функции и требуемой точности расчета.
Приведем конкретный пример вычисления определенного интеграла по формуле (5.21).
192

Пример 5.36.
Используя формулу Симпсона приближенно вычислим
интеграл |
, приняв n = 10. Заметим, что этот интеграл, |
как и интегралы из двух предшествующих примеров, является неберущимся. В данном случае 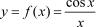 ;
;
По формуле (5.21) получим:
19

5.6.Понятиеодвойноминтеграле
Понятие двойного интеграла является расширением понятия определенного интеграла на случай двух аргументов.
На плоскости х0у рассмотрим замкнутую область В (область В называется замкнутой, если она ограничена линией и точки, которые лежат на границе, считаются принадлежащими области В), ограниченную линией L. В этой области зададим непрерывную функцию z = f (x, y). Область В произвольно разобьем на n частей (площадок): b1, b2, b3, …, bn. Площади этих частей (площадок) обозначим DS1, D S2, …, D Sn. В каждой площадке bi 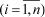 возьмем произвольную точку Mi (эта точка может лежать и на границе площадки). Таким образом, будем иметь n точек: М1, М2, …, Мn (см. рис. 5.22).
возьмем произвольную точку Mi (эта точка может лежать и на границе площадки). Таким образом, будем иметь n точек: М1, М2, …, Мn (см. рис. 5.22).
y |
L |
|
B вся область

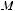 i
i
bi |
x |
|
0
Рис. 5.22
Через f (M1), f (M2), …, f (Mn) обозначим значения функции z = f (x, y) в выбранных нами точках. Затем составим сумму произведений f (Mi)DSi, которую обозначим Vs:
194
(5.22) |
Сумма (5.22) называется интегральной суммой для функ- |
ции z = f (x, y) в области В [22]. |
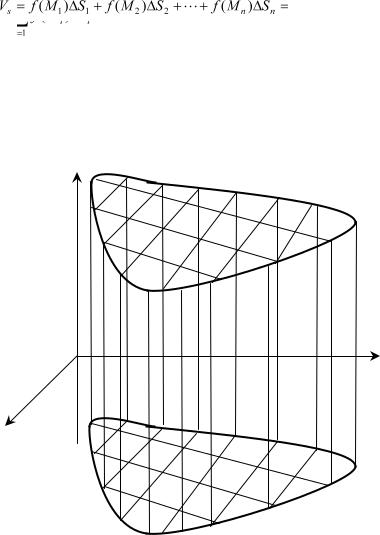
В случае, если z = f (x, y) $ 0 в области В каждое слагае- |
мое f (Mi)DSi есть объем цилиндра, площадь основания которого |
DSi, а высота f (Mi). А сумма Vs представляет собой объем неко- |
торого ступенчатого тела (см. рис. 5.2 ). |
y |
x |
0 |
z |
Рис. 5.23 |
Теперь рассмотрим произвольную последовательность ин- |
тегральных сумм, которые составлены с использованием фун- |
кции z = f (x, y) для области В: |
195

(5.2 )
при различных способах разбиении области В на площадки bi. Потребуем, чтобы максимальный диаметр площадок bi стремился к нулю (max diam bi → 0) при стремлении к бесконечности количества этих площадок (nk → `). Тогда будет справедлива следующая теорема, которую приводим без доказательства.
Теорема 5.4. Если функция z = f (x, y) непрерывна в замкнутой области В, то существует предел последовательности (5.2 ) интегральных сумм (5.22), если максимальный диаметр площадок bi → 0, а n → `. Этот предел будет одинаков для любой последовательности вида (5.2 ), т. е. он не зависит ни от способа разделения области В на площадки bi, ни от выбора в этих площадках точек Mi. Этот предел называется двойным интегралом от функции z = f (x, y) по области В и обозначается
т. е.
Область В называется областью интегрирования.
Если z = f (x, y) $ 0, двойной интеграл от этой функции по области В равен объему тела, ограниченного поверхностью z = f (x, y), плоскостью х0у и цилиндрической поверхностью, образующие которой параллельны оси 0z, а направляющей служит линия L.
Свойствадвойногоинтеграла
1) Если область В разбить на две части В1 и В2, то
Аналогично при разбиении области В на число частей больше двух.
196
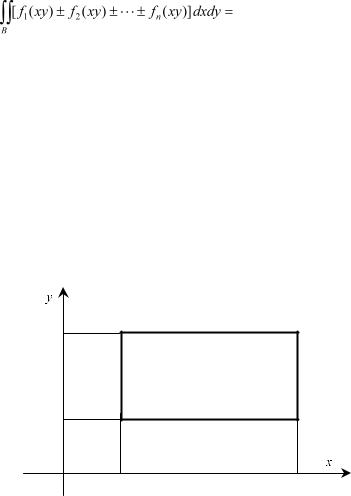
2) Двойной интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме двойных интегралов от этих функций, т. е.
) Постоянный множитель можно выносить за знак двойного интеграла, т. е.
где с — постоянная величина.
Вычислениедвойногоинтеграла
1. Простейший случай.
Область В задана неравенствами a # x # b, c # y # d, т. е. она является прямоугольником ADBC (см. рис. 5.24).
d |
D |
B |
|
|
|
c |
A |
C |
|
||
0 |
a |
b |
|
|
Рис. 5.24 |
В этом случаи двойной интеграл вычисляется по одной из приводимых ниже формул [2, 22]:
197

(5.24)
(5.25)
В правых частях формул (5.24) и (5.25) стоят повторные интегралы.
При вычислении по формуле (5.24) сначала находится оп-
ределенный интеграл |
, причем у рассматривается как |
постоянная, но результат интегрирования рассматривается как функция от у. Второе интегрирование в пределах от с до d выполняется по аргументу у. При использовании формулы (5.25) порядок действий обратный.
Двойной интеграл  есть объем призматичес-
есть объем призматичес-
кого тела с основанием ADBC. Заметим, что внешние знаки интеграла соответствуют внешним дифференциалам.
Рассмотрим конкретные примеры. Вычислить интегралы:
Пример 5.37.
Пример 5.38.
198
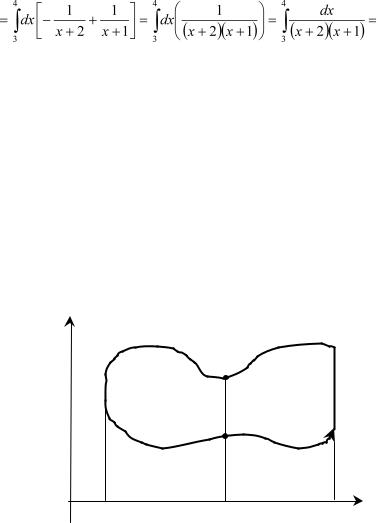
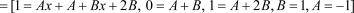 , получаем
, получаем
2. Общий случай.
а) Если контур области В встречается с любой пересекающей его вертикальной прямой не более чем в двух точках (т. N1 и т. N2 на рис. 5.25), то область В задается неравенствами a # x # b и w1(х) # y # w2(х),
y
y=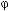 2(x) B2
2(x) B2
N2 B
A
N1 B1
y=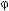 1(x)
1(x)
0 |
a |
N |
b x |
Рис. 5.25
где a и b — крайние абсциссы области В;
w1(х) и w2(х) — функции, выражающие ординаты нижней и верхней граничных линий AN1B1 и AN2B2.
199
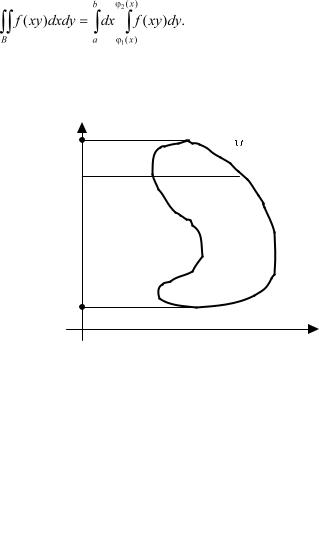
В этом случае двойной интеграл находится по формуле
[2, 22]:
(5.26)
б) Если контур области В встречается не более чем в двух точках с любой пересекающей его горизонтальной прямой, то аналогично случаю а) получаем (см. рис. 5.26).
y |
D |
d |
x= 2(y) |
|
|
K1 |
K2 |
K |
|
B
x=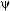 1(y)
1(y)
cC
0 |
x |
Рис. 5.26
(5.27)
Если контур области В не подходит ни под случай а), ни под случай б), то ее разбивают на несколько частей так, чтобы к каждой части были применимы или формула (5.26) или (5.27).
Рассмотрим конкретный пример.
Пример 5.39.
Вычислим интеграл |
, если область В огра- |
ничена линиями у = х2, у2 = х (см. рис. 5.27). Данная задача подходит под случаи а) и б).
200
