baldin_kv_red_matematika_dlia_gumanitariev

Рассмотрим систему уравнений (2. ), которую запишем в матричном виде

—вектор свободных членов;

—вектор неизвестных.

Если определитель матрицы А (det А) не равен нулю, то существует A–1.

Домножим слева систему (2.10) на A–1, получим

A–1 AX = A–1B, так как A–1A = E, то

имеем EX = A–1B, а так как EX = X, то

окончательно получим X = A–1 B (2.11) или в развернутом виде

(2.12)

Из (2.12) следует

71

(2.1 )

Числители равенств (2.1 ) есть разложения по элементам 1, 2, …, n-го столбцов определителя, полученного из det А заменой в нем 1, 2, …, n столбцов столбцом свободных членов, т. е.

Таким образом, неизвестные xi можно найти по формуле

(2.14)

где i = 1, 2, …, n. [19].

Решим систему уравнений, используя метод Крамера

Пример 2.4.

Вначале найдем определитель исходной системы

Затем находим

72

и определяем неизвестные xi; i = 1, 2, :

2.3.собственныечислаисобственныевекторыматриц

Проблема собственных чисел играет существенную роль не только в линейной алгебре, но и в других разделах математики, а также во многих прикладных областях (в менеджменте, психологии, юриспруденции) [12].

Пусть задана квадратная матрица А размера (n n), элементами которой являются действительные числа (R) и вектор неизвестных Х размера (n 1):

Предположим, что l — это некоторое неизвестное действительное число.

Если l и ненулевой вектор Х удовлетворяют уравнению

7

то l называется собственным числом или собственным значением матрицы А, а Х — собственным вектором этой же матрицы, соответствующим l [12, 15].

Преобразуем уравнение (2.15) к следующему виду:

где Е — единичная матрица. Матрица

называется характеристической матрицей [18].

Так как по условию вектор неизвестных Х не равен нулю, то среди его координат x1, x2, …, xn должна быть хотя бы одна ненулевая. А для того, чтобы система линейных однородных уравнений (2.16) имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен нулю (это следует из теоремы Кронекера-Капелли).

Поэтому получаем

(2.17)

Число l= lk, где 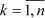будет собственным числом только в том случае, если матрица (lkE – A) — вырожденная.

Уравнение (2.17) называется характеристическим уравнением матрицы А и представляет собой алгебраическое уравнение степени n относительно l [18]:

74

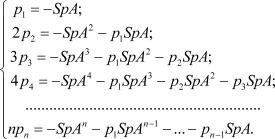
Уравнение (2.18) имеет n корней l1, l2, …, ln. Множество всех корней уравнения (2.18) называется спектром матрицы А.

Заметим, что уравнение det (A – lE) = 0 имеет те же корни, что и уравнение (2.17), т. е.

det (A – lE) = (–1)n det (lE – A).

Каждому собственному значению спектра матрицы А ставится в соответствие собственный вектор, определенный с точностью до скалярного множителя. Если lk есть кратный корень характеристического уравнения, то для произвольной квадратной матрицы число соответствующих собственных векторов может быть не равно кратности корня. С геометрической точки зрения собственный вектор определяет в пространстве некоторое направление (прямую, проходящую через начало координат), которое в результате преобразования не изменяется и вдоль которого пространство испытывает растяжение или сжатие в l раз [ , 18].

Полином ln + p1ln–1 + … + pn = 0 называют характеристическим полиномом. Коэффициенты pk 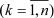можно вычислить по следующим рекуррентным формулам [29]:

(2.19)

Здесь — след матрицы (сумма элементов, стоя-

щих на главной диагонали матрицы А). Заметим, что pn = (–1)ndet A. При отыскании собственных чисел даже для матриц невысокого порядка неизбежно большое количество вычислений. Для общего случая нельзя предложить оптимальный способ нахождения собственных чисел и собственных векторов матрицы.

75

Рассмотрим случай, когда собственные числа находятся сразу исходя из вида матрицы (исходная матрица либо диагональная, либо верхняя или нижняя треугольная). В этом случае собственные числа l1, l2, …, ln совпадают с элементами главной диагонали исходной матрицы a11, a22, …, ann.

Пусть задана верхняя треугольная матрица А размера

(n n):

Тогда имеем

Отсюда видно, что собственные числа равны:

l1 = a11, l2 = a22, …, ln = ann.

С появлением ЭВМ получили распространение итерационные методы нахождения собственных чисел, которые не используют вычисление характеристического полинома. К этим способам относятся: степенной метод, метод обратных итераций, QR-алгоритм, метод вращений Якоби, QL-алгоритм и др. Причем применение конкретного итерационного метода зависит от вида исходной матрицы А [1].

Теперь рассмотрим конкретные примеры. Пример 2.5. Дана матрица А размера ( )

76

Найти собственные числа и собственные векторы матрицы А.

Из условия задачи видно, что матрица А является верхней треугольной матрицей. Поэтому собственными числами данной матрицы будут элементы ее главной диагонали

Теперь найдем соответствующие найденным собственным числам собственные векторы. Для этого мы используем урав-

нение (2.16).

Для l1 = –4 получаем

где

Далее раскроем матричное уравнение (2.20)

В результате получим

или

Так как матрица этой системы вырождена, то она имеет ненулевые решения, которые имеют вид:

77

т. е. получены искомые собственные вектора для l1 Для l2 = l = 1 получаем

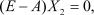где

или в подробной записи

В результате получаем

5х1 – 4х2 – х = 0 или х = 5х1 – 4х2,

т. е. это уравнение имеет ненулевые решения, которые и будут искомыми собственными векторами для l2.

Эти решения запишем в виде

Пример 2.6. Дана матрица А размера (2 2). Найти собственные числа и собственные матрицы А

Запишем характеристическое уравнение (2,17) для данного случая

Теперь найдем собственные векторы исходной матрицы А, соответствующие l1 = 1 и l2 = –4.

78

Для l1 = 1 имеем 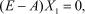где 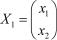В подробной записи получим

или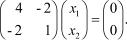

Так как определитель полученной матрицы равен нулю, то она имеет ненулевые решения, которые и являются собственными векторами Х1, которые мы и находим

Из первого уравнения системы получаем х2 = 2х1. Из второго уравнения системы получаем х2 = 2х1, т. е. она имеет бесконечное множество решений. И искомый собственный вектор Х1 будет иметь вид

Аналогично, для l2 = –4 находим

В заключение приведем два полезных правила [18]:

1)сумма собственных чисел матрицы А равна следу этой матрицы, т. е.

2)произведение собственных чисел матрицы А равно определителю этой матрицы

79

2.4.некоторыесведенияовекторах

Цифровые данные, используемые в экономике, можно представить в виде списков чисел, каждое из которых имеет определенный смысл.

Например, списки цен различных товаров в магазинах, объемы продукции разных видов, выпущенных каким-либо предприятием за год и т. д. В математике такие упорядоченные списки чисел называют векторами. Дадим определение n-мер- ного вектора (n = 1, 2, ….).

Упорядоченный набор n чисел x1, х2, х , …, хn называется n- мерным вектором. Мы будем обозначать векторы заглавными буквами со стрелками над ними, т. е.

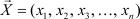, числа x1, х2, х , …, хn есть координаты вектора, а n — его размерность [12, 1 ].

Два n-мерных вектора называются равными, если их соответствующие координаты равны, например:

Вектор, все координаты которого нули, называется нольвектором и обозначается .

Алгебраической суммой двух n-мерных векторов

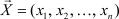и

называется вектор 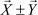, каждая координата которого равна алгебраической сумме соответствующих координат векторов 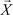и , т. е.

(2.21)

Произведением действительного числа k на n-мерный вектор 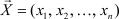называется n-мерный вектор , каждая координата которого равна произведению числа k на соответствующую координату вектора 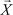, т. е.

(2.22)

Множество n-мерных векторов, для которых определены действия алгебраического сложения (2.21) и умножения на

80