1. Определение меры вариации статистической совокупности

На первом этапе необходимо определить, является ли совокупность значений определенного признака однородной. Существует несколько методов проверки совокупности на однородность. Так, для определения величины вариации признака рассчитываются такие статистические характеристики, как:

– размах R=x_max-x_min ; (3.2)

– коэффициент осцилляции 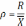; (3.3)

– коэффициент вариации 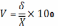(3.4)

Где 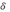- среднеквадратическое отклонение, равное квадратному корню из дисперсии.

Дисперсия является вторым центральным моментом распределения и представляет собой среднее значение отклонения индивидуальных значений признака от среднего:

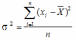(3.5)

Рассмотрим расчет характеристик статистической совокупности на примере. Для определения статистических характеристик заполним таблицу в диапазоне I2:N8 (рис. 31).

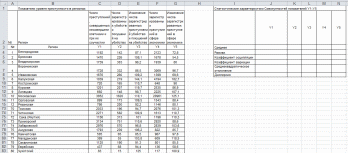
Рисунок 31. Фрагмент таблицы (БД) для расчета характеристик вариации

Для определения среднего значения используется функция =СРЗНАЧ(C4:C83).

Для определения размаха – =МАКС(C4:C83)-МИН(C4:C83). Для определения коэффициента осцилляции – =J4/J3.

Среднеквадратическое отклонение и дисперсию можно определить с помощью функций или формул. В таблице (рис. 32) это сделано с помощью функций =СТАНДОТКЛОНП(C4:C83) и =ДИСПР(C4:C83) соответственно.

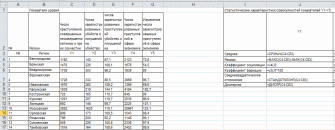
Рисунок 32. Формулы и функции расчета основных статистических характеристик

Пример расчета среднеквадратического (стандартного) отклонения и дисперсии показан на рис. 33. Лист отображен в режиме формул (СЕРВИС –ПАРАМЕТРЫ – ФОРМУЛЫ).

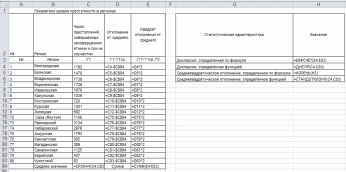
Рисунок 33. Пример расчета среднеквадратического (стандартного) отклонения

Алгоритм расчета среднеквадратического (стандартного) отклонения следующий:

1. В ячейке С84 определяем среднее значение показателя.

2. В диапазоне D4:D83 определяем отклонение текущего значения показателя от среднего, например, в ячейке D4: =C4-C$84.

3. В диапазоне Е4:Е83 рассчитываем квадрат каждого отклонения, например, в ячейке Е4: =D4^2.

4. В ячейке Е84 суммируем все квадраты отклонений: =СУММ(E4:E83).

5. В ячейку, например, Н3 вводим формулу определения дисперсии: =E84/СЧЁТ(E4:E83).

6. В ячейку Н5 вводим формулу расчета среднеквадратического отклонения: =КОРЕНЬ(H3).

Проверка с помощью функций определяемых статистических характеристик позволяет сделать вывод о правильности расчетов (рис. 34).

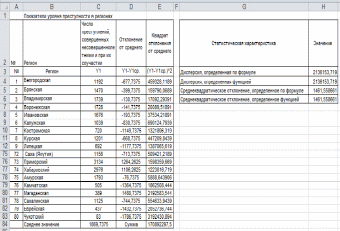
Рис. 34. Результаты расчета среднеквадратического (стандартного) отклонения и дисперсии значений показателя «Число преступлений, совершенных несовершеннолетними и при их соучастии» с помощью формул и функций

Степень однородности исследуемой совокупности определяется с помощью коэффициента вариации, расчет которого осуществляется по формуле (3.4): =J3/J6*100 (рис. 35).

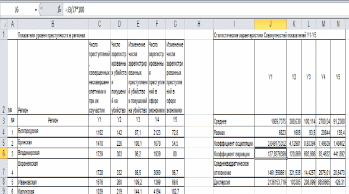
Рисунок 35. Результаты расчета коэффициента вариации и других статистических характеристик

Если коэффициент вариации менее 33 %, то совокупность можно считать однородной, в противном случае – неоднородной. Так как в нашем примере коэффициент вариации равен 127,9 %, можно сделать вывод о высокой степени неоднородности совокупности значений показателя «Число преступлений, совершенных несовершеннолетними и при их соучастии».

Следовательно, необходимо перейти к этапу выявления аномальных значений совокупностей (так называемых «выбросов»).