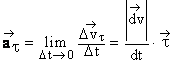25. Вынужденные электромагнитные колебания. Переменный ток

Электромагнитные колебания, происходящие в колебательном контуре под действием периодически изменяющейся э.д.с. источника переменного тока, подключенного к этому контуру, называют вынужденными.

Переменным называют ток, периодически изменяющийся по величине и по направлению. Иными словами, переменный ток это вынужденные электромагнитные колебания.

Переменный ток можно получить, используя проводящую рамку, вращающуюся в магнитном поле.

Пусть рамка вращается с постоянной угловой скоростью ω в однородном магнитном поле с индукцией В. Магнитный поток, пронизывающий рамку, Ф = ВS cosα. Угол α изменяется по закону α = ωt. Следовательно, Ф = ВS cos ωt.

Согласно закону электромагнитной индукции, ε = - N Ф', где N - число витков в рамке. Следовательно,

ε = - NBS(cos ωt)' = NBSω sinωt.

Обозначим NBSω = εm (εm - амплитудное значение э.д.с.)

Получаем для э.д.с., возникающей в рамке, выражение

ε = εm sinωt.

Следовательно, э.д.с. в рамке изменяется по гармоническому закону. Разделив обе части равенства на R, получим

i = Im sinωt,

где i - мгновенное значение силы переменного тока, Im - амплитудное значение силы тока.

Действующие значения силы переменного тока и напряжения находят по формулам:

;  .

Сопротивлением участка цепи переменного тока называют величину, равную отношению действующего (или амплитудного) значения напряжения на концах этого участка к действующему (или амплитудному) значению силы тока в данном участке цепи.

Одна и та же катушка индуктивности или конденсатор в цепи постоянного тока обладают одним сопротивлением, а в цепи переменного тока - другим сопротивлением. Следовательно, кроме активного сопротивления R в цепи переменного тока существуют и другие виды сопротивления.

Индуктивное сопротивление определяется по формуле XL = ωL.

Емкостное сопротивление рассчитывают по формуле XС = 

Установлено, что полное сопротивление Z, оказываемое переменному току цепью, содержащей активное, индуктивное и емкостное сопротивления, можно определить по формуле

https://xreferat.com/102/1023-5-fizika-osnovy-teorii.html

1.19. Центростремительное, тангенциальное и полное ускорения

 

Пусть в плоской системе координат (XOY) движется м.т., описывая криволинейную  траекторию.

В произвольный момент времени  t₁ материальная точка при движении со скоростью   находится  в пункте А. В следующий момент  времени t₂, она находится в  точке В, имея скорость   (рис. 1.16).

Если интервал времени  Δt мал, то участок криволинейной траектории  представляет собой некоторую дугу  АЕ, которая в пределе может совпасть с дугой некоторого круга кривизны радиуса R с центром в точке О.

Скорости    и    отличаются и по величине, и по направлению, т.е.

      и    v₁ ≠ v₂.

Перенесём вектор   (можно и вектор  ) параллельно самому себе так, чтобы совпали начала векторов   и    в точке А. Соединим концы этих векторов направленным отрезком ВД и обозначим его  .

Рис.1.16

Вектор   (рис. 1.16) является вектором изменения (приращения) скорости  за  время Δt и характеризует изменение скорости как по величине, так и по направлению.

На отрезке АВ (модуль вектора  ) отложим отрезок АС, равный по величине модулю вектора  . Соединим точки С и Д направленным отрезком, который обозначим вектором   , характеризующий изменение скорости только по направлению. Направленный отрезок ВС назовем вектором  , характеризующим изменение скорости по  величине.

Таким образом, если вектор   характеризует изменение скорости за время t и по величине и по направлению, то вектор   характеризует изменение скорости только по направлению, а вектор   - только по величине,  т.е.  .

                           

Согласно рис. 1.16

.

(1.33)

 

Из подобия равнобедренных треугольников ΔОАЕ и ΔАСД, где модуль   - хорда АЕ, следует, что

,

где  ,  так как  . После преобразования  , поскольку R и v² = сonst.

В связи с тем, что изменение скорости   произошло за время Δt, разделим левую и правую части на Δt:     .

По определению мгновенного ускорения, имеем: слева - вектор полного ускорения   , справа - первое слагаемое

,

(1.34)

второе слагаемое

.

(1.35)

   Тогда

.

(1.36)

(1.37)

аn = v2/R,

(1.38)

где   - единичный вектор нормали к дуге окружности. Он направлен по радиусу к центру круга кривизны (рис.1.17), т.к. с переходом к пределу, когда точки А и Е сливаются, скорость    приближается к    и угол  α  → 0.

Соответственно углы: АСД и АДC равны (как углы при основании равнобедренного треугольника) и стремятся к 90^о. Следовательно, в пределе  вектор   (   или   )  направлен по радиусу к центру круга кривизны и называется   центростремительным (нормальным)  ускорением.

 

Рис. 1.17

 

Вектор центростремительного ускорения характеризует изменение скорости по направлению. Направлен по радиусу к центру круга кривизны.

Рассмотрим вторую составляющую полного ускорения. Вектор

(1.39)

называют  тангенциальным (касательным) ускорением, где   - единичный вектор, направленный  по касательной к траектории, т.е.

  .

Вектор касательного (тангенциального) ускорения характеризует изменение скорости по величине, направлен по касательной к траектории в данной точке.

При произвольном криволинейном движении материальной точки полное ускорение   может быть   разложено на две составляющие: и  , где  .

Вектор полного ускорения характеризует изменение скорости по величине и направлению, направлен внутрь кривизны траектории.

Модуль полного ускорения

.

(1.40)

Возникновение  нормального и тангенциального ускорений наблюдается при движении искусственных спутников Земли, которые, двигаясь по орбите (эллиптическая  траектория), должны всё время изменять свою скорость не только по направлению, но и по величине, так как нормальное ускорение в любой точке траектории направлено по радиусу к центру Земли.

http://files.lib.sfu-kras.ru/ebibl/umkd/u_course/Lekc/Part1/Glava1/19.htm

Криволинейное движение

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.

Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции v_xи v_y ее скорости на оси Ox и Oy и координаты x и  y точки в любой момент времени t определяется по формулам

   

   

Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением   где r – радиус окружности.

Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.

При криволинейном движении ускорение можно представить как сумму нормальной    и тангенциальной    составляющих:

 ,

  - нормальное (центростремительное) ускорение, направлено к центру кривизны траектории и характеризует изменение скорости по направлению:

v – мгновенное значение скорости,   r – радиус кривизна траектории в данной точке.

  - тангенциальное (касательное) ускорение, направлено по касательной к траектории и характеризует изменение скорости по модулю.

Полное ускорение, с которым движется материальная точка, равно:

 .

Кроме центростремительного ускорения, важнейшими характе­ристиками равномерного движения по окружности являются период и частота обращения.

Период обращения— это время, за которое тело совершается один оборот.

Обозначается период буквой Т (с) и определяется по формуле:

где t — время обращения, п — число оборотов, совершенных за это время.

Частота обращения— это величина, численно равная числу оборотов, совершенных за единицу времени.

Обозначается частота греческой буквой   (ню) и находится по формуле:

Измеряется частота в 1/с.

Период и частота — величины взаимно обратные:

Если тело, двигаясь по окружности со скоростью v, делает один оборот, то пройденный этим телом путь можно найти, умножив ско­рость v на время одного оборота:

l = vT. С другой стороны, этот путь равен длине окружности 2πr. Поэтому

vT = 2πr,

где w (с^-1) - угловая скорость.

При неизменной частоте обращения центростремительное ускорение прямо пропорционально расстоянию от движущейся частицы до центра вращения.

Угловая скорость (w) – величина, равная отношению угла поворота радиуса, на котором находится вращающаяся точка, к промежутку времени, за который произошел этот поворот:

 .

 

Связь между линейной и угловой скоростями:

v= wr.

Движение тела можно считать известным лишь тогда, когда известно, как движется каждая его точка. Самое простое движение твердых тел – поступательное. Поступательным называется движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе

http://sfiz.ru/page.php?id=117

1. Кинематика материальной точки. Системы отсчета. Траектория, перемещение, путь, скорость, ускорение. Равномерное и равнопеременное прямолинейные движения

Кинема́тика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение. Системы отсчета: Инерциальная и неинерциальная Система отсчёта — это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел. Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятся. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике: «Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным». Законы Ньютона, а также все остальные аксиомы динамики в классической механике формулируются по отношению к инерциальным системам отсчёта. Абсолютно инерциальные системы представляют собой математическую абстракцию и в природе не существуют. Траекто́рия материа́льной то́чки — линия в пространстве, вдоль которой движется тело, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта. Перемеще́ние (в кинематике) — изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Мгновенная скорость точки определяется как предел отношения перемещения к малому промежутку времени, за которое оно совершено. Путь- длина участка траектории материальной точки в физике. Ско́рость — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта; по определению, равна производной радиус-вектора точки по времени v=dr/dt, r-радиус-вектор Ускоре́ние — физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени. Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости v тела при его движении за единицу времени: a=dv/dt Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением.

К оглавлению

2. Криволинейное движение. Нормальное и тангенциальное ускорения

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению. Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту). Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение: Aτ=lim(ΔVτ/Δt) Δt->0 или Aτ=(Vτ-V0)/(t-t0) Где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0 соответственно. Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему. Нормальное ускорение - это изменение скорости по направлению за единицу времени: An=lim(ΔVn/Δt) Δt->0 Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости. Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности. Полное ускорение при равнопеременном криволинейном движении тела равно: a=sqrt(aτ^2+an^2)

К оглавлению

3. Движение точки по окружности

Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения удобно рассматривать угловое перемещение Δφ (или угол поворота) измеряемое в радианах (рис. 1.6.1). Длина дуги связана с углом поворота соотношением  Δl = RΔφ. При малых углах поворота Δl ≈ Δs. Угловой скоростью ω тела в данной точке круговой траектории называют предел (при Δt → 0) отношения малого углового перемещения Δφ к малому промежутку времени Δt:  [img]http://www.physics.ru/courses/op25part1/content/javagifs/63229980753953-4.gif[/img] Угловая скорость измеряется в рад/с. Связь между модулем линейной скорости υ и угловой скоростью ω:  υ = ωR. При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора  Равномерное движение тела по окружности является движением с ускорением. Ускорение  [img]http://www.physics.ru/courses/op25part1/content/javagifs/63229980753983-6.gif[/img]направлено по радиусу к центру окружности. Его называют нормальным или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями:  [img]http://www.physics.ru/courses/op25part1/content/javagifs/63229980753993-7.gif[/img] Вывод формул:[url=http://www.physics.ru/courses/op25part1/content/chapter1/section/paragraph6/theory.html]http://www.physics.ru/courses/op25part1/content/chapter1/section/paragraph6/theory.html[/url]

К оглавлению

4. Динамика материальной точки. Инерциальные системы отсчета и первый закон Ньютона

Первый закон Ньютона гласит: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Первый закон Ньютона показывает, что состояние покоя или равномерного прямолинейного движения не требует для своего поддержания внешних воздействий: В этом проявляется особое динамическое свойство тел, называемое инертностью. Соответственно первый закон Ньютона обычно называют законом инерции, а движение тела, свободного от внешних воздействий - движением по инерции. Опыт показывает, что первый закон Ньютона выполняется не во всякой системе отсчета. Системы отсчета, по отношению к которым выполняется закон инерции, называются инерциальными системами отсчета. То есть, это такие системы отсчета, относительно которых материальная точка, на которую не действуют другие тела, либо покоится, либо движется равномерно и прямолинейно. Системы отсчета в 1 вопросе

http://shpora.org/discipline/fizika/shpora/2803/