Постулаты Эйнштейна для сто. Преобразования Лоренца.

В основе специальной теории относительности лежат два принципа или постулата, сформулированные Эйнштейном в 1905 г.

Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна.

Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую.

«Преобразования Лоренца» возникли на рубеже XIX-XX веков как формальный математический прием для согласования электродинамики с механикой и легли в основу специальной теории относительности. Согласно этим преобразованиям длины и промежутки времени искажаются при переходе из одной системы отсчета в другую. Эти эффекты получили известность как сокращение Лоренца и замедление времени.

Преобразования Лоренца сложнее, чем преобразования Галилея:

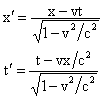
В этих формулах x и t – положение и время в условно неподвижной системе отсчета, x′ и t′ - положение и время в системе отсчета, движущейся относительно неподвижной системы равномерно и прямолинейно со скоростью v. Разумеется, что при малых скоростях, много меньших скорости света c, преобразования Лоренца переходят в преобразования Галилея.

 

Относительность понятия одновременности. Относительность длин и промежутков времени. Интервал между событиями. Его инвариантность. Причинность.

Одновременность - существование разных событий в один и тот же момент времени.

В классической физике признавалась абсолютная одновременность событий, протекающих в сколь угодно удаленных друг от друга точках мирового пространства. Это означало, что все события мироздания однозначно делятся на прошедшие, настоящие и будущие.

Подобные представления оставались общепринятыми, пока не появилась позитивистская идея о необходимости их экспериментальной проверки и обоснования. Анализ показал, что в их основе лежит только априорная уверенность в том, что одновременными являются те события, которые могут быть охвачены единым актом сознания. В реальной действительности абсолютная одновременность и однозначное деление всех событий на прошедшие, настоящие и будущие оказываются эмпирически достоверными только при условии, что взаимодействие и обмен информацией между событиями происходит с бесконечной скоростью. При любых конечных скоростях взаимодействия требование эмпирической проверяемости временных отношений между событиями приводит к появлению класса событий, между которыми не существует отношения "раньше (позже), чем", и характер временных отношений между ними оказывается неопределенным.

В специальной теории относительности (СТО) одновременные пространственно удаленные друг от друга события выявляются в ходе синхронизации связанных с этими событиями часов. Предложенная А. Пуанкаре и использованная А. Эйнштейном при разработке СТО процедура синхронизации пространственно удаленных друг от друга часов сводится к следующему.

1. Относительность одновременности событий

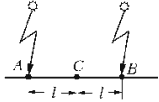 Принято считать, что события в точках A и B произошли одновременно, если световые сигналы, испущенные ими, приходят одновременно в точку C, находящуюся посередине между точками A и B.

Допустим, что в точке C находится покоящийся относительно A и B фотоэлемент, соединенный с осциллографом. При включении ламп световые сигналы к фотоэлементу приходят одновременно через некоторый промежуток времени   , и на экране осциллографа наблюдается один всплеск.

Пусть фотоэлемент с осциллографом движется равномерно со скоростью v влево, тогда световая волна от правой лампы должна будет пройти до фотоэлемента большее расстояние (l + s), чем волна от левой лампы (l – s), где s = vt. Это приведет к тому, что световая волна от левой лампы дойдет до фотоэлемента раньше, чем от правой, и на экране появятся два всплеска. Следовательно, события, одновременные в одной инерциальной системе отсчета, не являются одновременными в другой системе отсчета, т.е. одновременность событий относительна.

2. Относительность промежутков времени

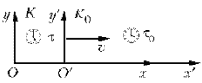 Пусть инерциальная система отсчета K покоится, а система отсчета K₀ движется относительно системы K со скоростью v.

Пусть интервал времени между двумя событиями, происходящими в одной и той же точке инерциальной системы K₀, равен t₀.

Тогда интервал времени между этими же событиями в системе K будет выражаться формулой: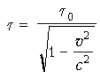 

Это эффект замедления времени в движущихся системах отсчета. Если v << c, то величиной   можно пренебречь, тогда   и никакого замедления в движущихся системах можно не учитывать.

Замедление времени позволяет, в принципе, осуществить «путешествие с будущее». Пусть космический корабль, движущийся со скоростью v относительно Земли, совершает перелет от Земли до звезды и обратно. За время t0 свет проходит путь от Земли до звезды:

l₀ = c • t₀.

Продолжительность полета по часам земного наблюдателя равна: 

Настолько постареют люди на Земле к моменту возвращения космонавтов. По часам, установленным на космическом корабле, полет займет меньше времени: 

По принципу относительности, все процессы на космическом корабле, включая старение космонавтов, происходят так же, как и на Земле, но не по земным часам, а по часам, установленным на корабле. Следовательно, к моменту возвращения на Землю космонавты постареют только на время t₀.

Если, например, t₀ = 500 лет и v²/c² = 0,9999, то формулы дают t = 1000,1 года, t₀ = 14,1 года.

Космонавты возвратятся на Землю, по земным часам спустя 10 веков после вылета и постареют лишь на 14,1 года.

3. Относительность расстояний

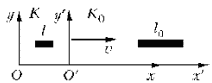 Расстояние не является абсолютной величиной, а зависит от скорости движения тела относительно данной системы отсчета. Рассмотрим две системы отсчета.

Обозначим через l₀ длину стержня в системе отсчета K₀, относительно которой стержень покоится. Тогда длина l этого стержня, измеренная в системе отсчета K, относительно которой стержень движется со скоростью v, определяется формулой:

Длина стержня зависит от того, в какой системе отсчета она измеряется. Один и тот же стержень имеет различную длину в различных системах отсчета. Максимальную длину l₀ стержень имеет в системе отсчета, в которой он покоится. В системах же, движущихся по отношению к стержню, он имеет длину тем меньшую, чем больше скорость движения. Если рассматривать движущееся тело, то сокращаются только его продольные размеры.

Интервал в теории относительности — расстояние между двумя событиями в пространстве-времени. Интервал не меняется при переходе от одной инерциальной системы отсчета к другой, что позволяет чисто формально получить преобразования Лоренца как группу преобразований, сохраняющих интервал. Также инвариантность интервала служит основой для введения пространства Минковского, в котором смене инерциальных систем отсчета соответствуют "вращения" этого пространства.

Интервал является одним из фундаментальных физических понятий. Он лежит в основе специальной и общей теорий относительности. Свойство теории сохранять интервал при смене инерциальной системы отсчета называется Лоренц-инвариантностью.

Инвариантность интервала

Используемые постулаты

Напрямую из принципа относительности, однородности и изотропности пространства, а также однородности времени следует, что при переходе от одной ИСО (инерциальной системы отсчета) к другой ИСО интервал остается неизменным. Именно это его свойство позволяет формально вывести преобразования Лоренца и обосновывает оправданность введения пространства Минковского и неримановой метрики.

Особо подчеркнем, что для приведенного доказательства инвариантность скорости света значения не имеет! Важно лишь, что максимальная скорость распространения взаимодействий существует и одинакова во всех системах отсчета. Одинаковость этой скорости следует из принципа относительности. Для краткости, в дальнейшем доказательстве под интервалом будем подразумевать интервал между двумя бесконечно близкими в пространстве и времени событиями, а под скоростью света - максимально возможную скорость распространения взаимодействий. Оказывается, что свет распространяется именно с такой скоростью, обозначаемой C.

https://lektsii.org/15-21988.html