Момент импульса. Уравнение моментов. Закон сохранения момента импульса.

Моментом импульса т. наз. величина физически равная векторному произведению радиуса вектора т. на ее импульс L=[r*p] p=mV L=[r*mV] L=Iw lw –напр. в одну сторону.

Момент импульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.

Момент импульса замкнутой системы сохраняется.

Момент импульса   частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса:

где   — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта,   — импульс частицы.

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Уравнение моментов. Найдем скорость изменения момента импульса тела.

dL/dt = ([dr_i/dt·p_i] + [r_i·dp_i/dt]). (7.4)

Первое слагаемое в выражении (7.4) равняется нулю, поскольку производная от радиуса по времени, являющаяся скоростью i^ой части тела, параллельна ее импульсу. Второе слагаемое преобразуем, воспользовавшись 2^ым законом Ньютона:

dp_i/dt = F_i + F_ik*, где F_i и F_ik* - соответственно сумма внешних и внутренних силы, действующие на i^ый элемент тела.

Подставив это выражение в (7.4), получим, что скорость изменения момента импульса равняется сумме моментов внешних M_i и внутренних M_ik* сил. Причем, последний из них равен нулю. Таким образом,

dL/dt = (M_i + M_i*) = M_i = M. (7.5)

Следовательно, скорость изменения момента импульса вращающегося тела равняется суммарному моменту внешних сил, действующих на него.

Уравнение (7.5) называется уравнением вращательного движения в форме моментов (уравнением моментов).

Закон сохранения момента импульса: Если на систему вращающихся вокруг оси тел не действуют моменты внешних сил (система в этом смысле замкнута) или внешние моменты взаимно уравновешиваются, то суммарный момент импульса системы относительно оси вращения с течением времени не изменяется. Таким образом, закон утверждает, что внутренние моменты сил системы не в состоянии изменить полный суммарный момент импульса системы тел, а в состоянии лишь перераспределить его. Внутри системы возможна лишь передача момента импульса от тела к телу. В аналитическом виде закон сохранения момента импульса записывается следующим образом: если Mвнеш = 0 , то   или так: для начального и конечного момента времени

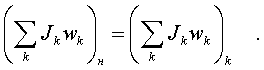
 https://lektsii.org/15-21986.html

Работа силы при вращении твердого тела. Кинетическая энергия вращающегося тела.

Работа и мощность при вращении твердого тела.

Найдем выражение для работы при вращении тела. Пусть сила   приложена в точке   , находящейся от оси   на расстоянии   ,   — угол между направлением силы и радиус-вектором   . Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол   точка приложения   проходит путь   и работа равна произведению проекции силы на направление смещения на величину смещения:

 .

Модуль момента силы равен:

 ,

тогда получим следующую формулу для вычисления работы:

 .

Таким образом, работа при вращении твердого тела равна произведению момента действующей силы на угол поворота.

Кинетическая энергия вращающегося тела.

Моментом инерции мат.т. наз. физ. величина численно равная произведению массы мат.т. на квадрат расстояния этой точки до оси вращения.W_ki =m_iV²_i/2 V_i -Wr_i Wi=miw²r²_i/2 =w²/2*m_ir_i²I_i=m_ir²_i момент инерции твердого тела равен сумме всех мат.т I=S_im_ir²_i моментом инерции твердого тела наз. физ.величина равная сумме произведений мат.т. на квадраты расстояний от этих точек до оси. W_i-I_iW²/2 W_k=IW²/2

W_k =S_iW_ki момент инерции при вращательном движении явл. аналогом массы при поступательном движении. I=mR²/2