14.Закон всемирного тяготения. Гравитационное поле и его характеристики. Потенциал поля. Связь между потенциалом и напряжённостью поля. Космические скорости.

Закон всемирного тяготения был открыт англичанином И. Ньютоном в 1666г. Закон звучит следующим образом: сила гравитационного притяжения двух материальных точек прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. В виде формулы это записывается так: F=G*m₁*m₂/r² где G — гравитационная константа, определяемая экспериментально 6,67 × 10^–11 Н·м²/кг²

ГРАВИТАЦИОННОЕ ПОЛЕ (поле тяготения), один из видов поля физического, посредством которого осуществляется гравитационное взаимодействие (притяжение) тел.

Гравитационное взаимодействие осуществляется через гравита­ционное поле. Всякое тело изменяет свойства окружающего его пространства — создает в нем гравитационное поле. Это поле проявляет себя в том, что помещенное в него другое тело оказывается под действием силы. Об «интенсивности» гравитационного поля, очевидно, можно судить по величине силы, действующей в данной точке на тело с массой, равной единице. В соответствии с этим величину называют Напряженностью гравитационного поля.

G=F/m

Величину φ=U/m’ называют потенциалом гравитационного поля. В этой формуле U есть потенциальная энергия, которой обладает материальная точка массы m’ в данной точке поля.

Потенциал – скалярная величина, поэтому пользоваться и вычислять φ проще, чем   .

Формулу   можно использовать для установления единиц потенциала: за единицу φ принимают потенциал в такой точке поля, для перемещения в которую из бесконечности единичного положительного заряда необходимо совершить работу равную единице.

В физике часто используется единица энергии и работы, называемая электрон - вольт (эВ) – это работа, совершенная силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов 1 В.

Первая космическая скорость

Для осуществления равномерного движения по окружности радиуса r его горизонтально направленная скорость должна иметь такое значение v, при котором центростремительное ускорение равно ускорению свободного падения

 (1). Из (1) следует:  (2). Скорость V, при которой тело может двигаться по круговой орбите вокруг Земли, называется первой космической скоростью. Из формулы (2) для значения r, равного радиусу Земли, r = 6371 км, первая космическая скорость равна

V = 7.9*10³ м/с При начальной скорости меньше 7,9 км/с тело, брошенное горизонтально, пролетев некоторое расстояние, упадет на поверхность Земли. При скорости 7,9 км/с в отсутствии воздуха оно будет двигаться вокруг Земли по окружности, став ее искусственным спутником. Вторая космическая скорость При небольшом превышении первой космической скорости орбита спутника будет эллиптической, а при достижении скорости 11,2 км/с превращается в параболу, ветви которой уходят в бесконечность. Скорость, при которой тело способно преодолеть действия сил притяжения небесного тела и удалиться от него на бесконечно далекое расстояние, называется второй космической скоростью. Из формулы (2) следует, что для вычисления первой космической скорости на расстоянии r от любого небесного тела, звезды или планеты, нужно знать ускорения a свободного падения на этом расстоянии от центра масс небесного тела. Небесное тело массой M действует на другое тело массой m на расстоянии r силой всемирного тяготения F. Следовательно, ускорение свободного падения тела на этом расстоянии равно  (3).

Из (2) и (3) первая космическая скорость V на расстоянии r от центра небесного тела массой M равна:

 (4). Формула (4) позволяет вычислять массы небесных тел, вокруг которых обращаются другие небесные тела под действием сил всемирного тяготения. Массу M Солнца можно найти по известным значениям скорости V движениям Земли по ее орбите и радиусу r земной орбиты:

    Скорость V движения Земли по орбите можно найти, зная радиус r земной орбиты и период Т ее обращения вокруг Солнца:   Для вычисления массы Солнца получаем формулу:  (5). Выразим период обращения Земли вокруг Солнца в единицах СИ:

T = 1 год = 3.16*10⁷ с Подставим числовые значения величин, найдем массу Солнца: M = 2*10³⁰ к Из формулы (5) следует, что для всех спутников, обращающихся по круговым орбитам вокруг одной планеты, или для всех планет, обращающихся вокруг одной звезды, отношение квадратов периодов обращения к кубам радиусов орбит является величиной одинаковой  (6). Равенство (6) выполняется и в случае движения спутников или планет по эллиптическим орбитам, если использовать как r большие полуоси эллипсов. 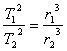Третий закон Кеплера Факт, что квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их эллиптических орбит, был открыт Иоганном Кеплером и называется третьим законом Кеплера:  (7).

https://lektsii.org/15-21985.html