Минимаксный принцип.

Пусть исследуемый объект может прибывать в двух состояниях ₁ и ₂, и мы можем принимать решения d₁ и d₂;

f ( x/d₁ ), f ( x/d₂ ) – заданы,

C₁₁=C₂₂=0 ; C₁₂, C₂₁ - заданы.

P₁ и P₂ - неизвестны.

P₂ = 1- P₁ ( то есть выполняется условие нормировки )

Запишем значение риска :

R = C₁₂P₁P₁₂ + C₂₁( 1-P₁ )P₂₁ - риск от P₁ зависит линейно.

Не имея возможности влиять на P₁, постараемся влиять на ( R ).

Для того, чтобы оценить возможность влиять на раскроем выражение для риска :

R = C₁₂P₁ ) dx + C₂₁( 1-P₁ ) ) dx ( 3 )

R / P₁ = C₁₂ )dx - C₂₁ ) dx = ( X₀ ) ( 4 )

С другой стороны R / P₁ = t_g изменяя значение X₀ можно влиять на угол . Допустим ( X₀ ) = 0 и найдем решение этого уравнения :

Для окончательного решения задачи нужно найти связь между X₀ и P₁.

R / X₀ = -C₁₂P₁f ( X₀/d₁ ) + C₂₁ ( 1-P₁ )f ( X₀/d₂ ) = 0 ( 5 )

Если в уравнении ( 5 ) подставить X₀, то равенство нулю может быть достигнуто только за счет определенного значения P₁.

P₁^* = P₁|_{Xo = Xo}^*

P₁^* = C₂₁ / C₂₁ + C₁₂ ( f (X_o^*/d₁) / f ( X_O/d₂) ) ( 6 )

R ( X^*,P₁^* ) = min max R

x_o {x_o} p₁ [a,b]

Теперь можно рассчитать величину:

= C₂₁ / C₁₂ P₂ / P₁ = C₂₁ / C₁₂ 1-P₁^* / P₁^*

Если известно, то вступает в действие принцип Байеса

min max R = C₁₂P₁^* )dx + C₂₁ ( 1-P₁^* ) ₂ ) dx

Формирование расчетных алгоритмов Алгоритм на основе байесовского принципа.

2.1.1. Исходные данные

₁=5 a₁=0.4361836 x={7: 9: 11}

₂=12 a₂=0.1201676

S₁=2 a₃=0.937298

S₂=3 b₁=0.33267

P₁=0.9

C₁₁=0

C₁₂=1

C₂₁=20

C₂₂=0

2.1.2

2.1.3

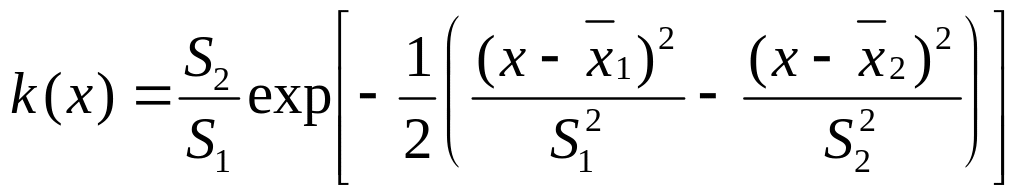
2.1.4 При

При

2.1.5

2.1.6

2.1.7

2.1.8

2.1.9

2.1.10

2.1.11

2.1.12

2.1.13

2.1.14

2.1.15

2.1.16

2.1.17

2.1.18

Алгоритм на основе минимаксимального принципа

2.2.1 Исходные данные

₁=5 a₁=0.4361836 x={7: 9: 11}

₂=12 a₂=0.1201676 =0.1

S₁=2 a₃=0.937298

S₂=3 b₁=0.33267

P₁=0.9

C₁₁=0

C₁₂=1

C₂₁=20

C₂₂=0

2.2.2

2.2.3

2.2.4

2.1.5

2.2.6

2.2.7

2.2.8

2.2.9

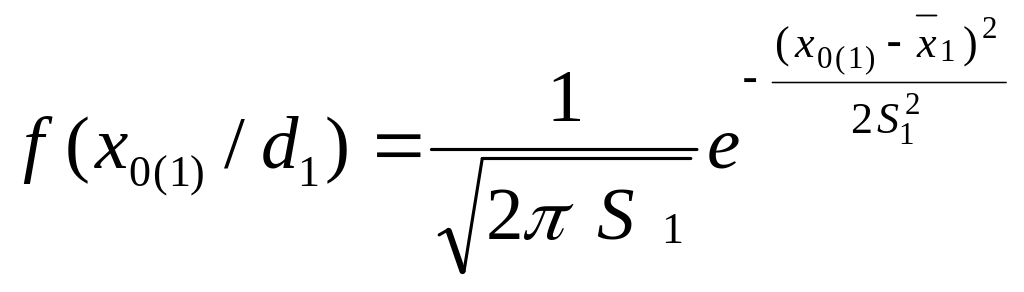
2.2.10

2.2.11

2.2.12

2.2.13 где n=2;3;.....;n^*

2.2.14 

2.2.15

2.2.16

2.2.17

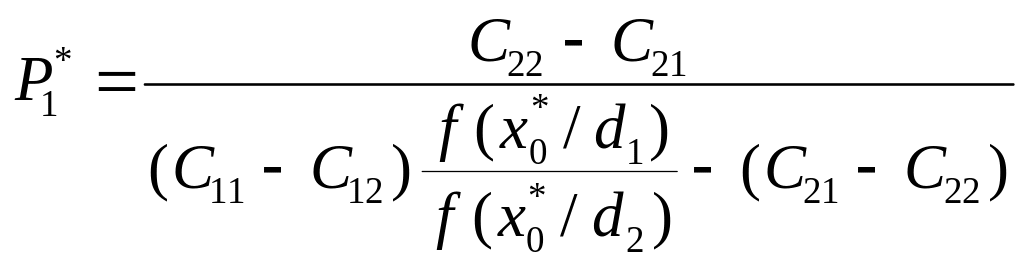
2.2.18

2.1.19

2.1.20 При

При

2.1.21

Рекомендации по выполнению работы.

Исходные данные:

Пусть f(x/d) является плотностью нормального распределения с параметрами (например):

_

x₁ - 5 г (5 г железа на I тонну масла),

S₁ - 2 г,

_

x₂ - 12 г,

S₂ - 3 г,

Кроме того, на основе анализа статистических данных установлено, что вероятность исправного состояния гидроцилиндра P₁= 0,9, т.е. P₂ = 1- P₁ = 0,1.

Примем также, что:

C₁₁ = C₂₂ = 0,

C₁₂= 1,

C₂₁= 20,

т.е. цена ошибки второго рода (цена пропуска дефекта) в 20 раз больше цены ошибки 1-го рода (цены ложной тревоги).

При этих исходных данных необходимо:

1. Определить параметры нормального распределения (оценку математического ожидания x и среднеквадратичного отклонения S для выборок, соответствующих исправному и неисправному состояниям гидроцилиндров):

_

x₁ , S₁ ,

_

x₂ , S₂ ,

по формулам:

Примечание: Эти параметры проще рассчитать, скопировав свой вариант в EXEL и воспользовавшись стандартными функциями «СРЗНАЧ» и «ДИСП» для своих выборок. Среднеквадратичное отклонение S получаем, извлекая корень из дисперсии (функция «КОРЕНЬ»).

Ввести полученные данные в соответствующие поля программы «tes_lab1».

Рис.2.

2. Определить (нажав кнопку «РАСЧЕТ») граничное значение x₀ и величину риска, используя байесовский принцип и метод минимакса.

3. Изменяя значение цены ошибки второго рода C₂₁, исследовать влияние C₂₁ на x_0., рассчитанное по байесовскому принципу и методу минимакса. Построить и проанализировать графики зависимости x₀=f(C₂₁). Сделать выводы.

4. Изменяя значение вероятности исправного состояния гидроцилиндра P₁, исследовать влияние P₁ на x_0., рассчитанное по байесовскому принципу и методу минимакса. Построить и проанализировать графики зависимости x₀=f(P₁). Сделать выводы.