Нормированная корреляционная функция стационарного процесса

Таблица 5

0	0.4	0.8	1.2	1.6	2.0	2.4
1	0,86	0,61	0,37	0,08	-0,22	0,53

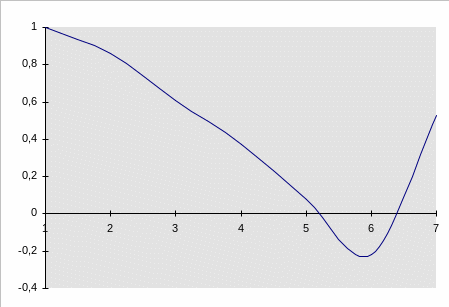
Вывод: Наличие отрицательных значений на графике указывает на то, что в структуре случайной функции имеется некоторый элемент периодичности, однако функция X(t) заменена стационарной функцией с параметрами: X(t)= 0,018±1,041.

Лабораторная работа № 4 Планирование эксперимента. Регрессионный анализ

Цель работы: Ознакомление с методом планирования эксперимента. Создание математической модели определения скорости предела сквозного пробития V_псп с использованием плана полнофакторного эксперимента.

Постановка задачи.

Рассматривается стрельба артиллерийским бронебойным снарядом по бронеплите. В качестве показателя эффективности действия БП-ов используется величина V_псп – скорость предела сквозного пробития. Показатель зависит от двух групп факторов (рис.1): конструктивных характеристик БП и их технологических отклонений. Из числа конструктивных характеристик учитываются:

d+d - калибр [м];

q+ q - масса [кг];

h_гч+ h_гч - высота головной части [м];

b+ b - толщина преграды [м];

_т+_т - предел текучести материала преграды [Па];

+ - плотность материала преграды [кг/м³];

d_т+ d_т - диаметр притупления головной части [м].

Рекомендуемые примерные отклонения параметров +:

калибр - до 0.5%;

масса - (2/3)%;

высота головной части - до 5%;

толщина преграды - до 0.5% ;

предел текучести мат. преграды - до 3% ;

плотность мат. преграды - до 1%;

диаметр притупления головной части до 1%.

5 количество опытов

Требуется, используя метод планирования эксперимента, Создать математическую модель определения скорости предела сквозного пробития V_псп в виде уравнения регрессии.

Сделать выводы по результатам исследования.

Рис.1 Расчетная схема.

Описание метода.

Сущность факторного эксперимента первого порядка состоит в одновременном варьировании всех факторов по определенному правилу, представлении математической модели в виде линейного полинома и исследовании последнего методами математической статистики.

Планирование эксперимента приобретает все большее значение при постановке исследований сложных систем в связи с необходимостью повышения эффективности и достоверности исследований. Четко провести эксперимент, объективно оценив сведения об изучаемом объекте и распространив материал, полученный в одном исследовании, на серию других исследований, можно только в том случае, если экспериментальные исследования правильно поставлены, а их обработка выполнена при обобщенном подходе.

Эксперименты обычно ставятся небольшими сериями по заранее составленному алгоритму, оптимальному в некотором строго сформулированном смысле. После каждой небольшой серии опытов производится обработка результатов наблюдений и принимается наиболее обоснованное решение о том, что делать дальше.

Чтобы получить математическую модель, используют факторный эксперимент, суть которого заключается в одновременном варьировании всех факторов объекта исследования по определенному плану.

Закодируем максимальные и минимальные значения факторов. Тогда все возможные комбинации факторов при варьировании на двух уровнях (минимальном и максимальном) будут определены четырьмя опытами. Такой план эксперимента принято записывать в виде матрицы планирования, где в первой строке спланирован первый опыт, когда факторам придаются минимальные значения; во второй строке - опыт, когда фактору 1 придают максимальное значение, а фактору 2 - минимальное, и т.д. Подобное планирование имеет ряд достоинств и поэтому широко применяется при получении моделей. Например, пользуясь планом, можно после проведения эксперимента определить коэффициенты линейного уравнения регрессии.

Уровнем фактора называют определенное значение фактора, которое будет фиксироваться при проведении эксперимента. Очевидно, уровнем фактора можно назвать и среднее значение рассматриваемой величины (переменной). Эти значения факторов называются нулевыми уровнями. Интервал варьирования - это такое значение фактора в натуральных единицах, прибавление которого к нулевому уровню дает верхний предел, а вычитание - нижний уровень фактора. Обозначим его . Очевидно, что интервал варьирования факторов должен составлять часть области определения факторов. Ограничение на интервал варьирования состоит в том, чтобы изменение фактора внутри этого интервала приводило к изменению значения функции отклика на величину, вдвое превышающую среднеквадратическую ошибку опытов. Это требование связано с тем, что интервал между двумя соседними уровнями должен значимо (не случайно) влиять на переменную состояния. Обычно интервал варьирования выбирается на основании априорной информации (или интуитивно) и затем уточняется (если он выбран неудачно) после получения математической модели. Алгоритм расчета включает с себя построение матрицы планирования, ее реализацию и статистическую обработку, которая состоит из дисперсионного и регрессионного анализа. Суть дисперсионного анализа заключается в разбиении общей дисперсии результатов (ошибки опытов) на составляющие, обусловленные влиянием тех или иных условий или факторов, и далее - в исследовании значимости составляющих дисперсии по сравнению с дисперсией воспроизводимости, связанной со случайным распределением. Простейшим видом дисперсионного анализа является оценка однородности дисперсий по критерию Кохрена. Регрессионный анализ сводится к определению на основании экспериментальных данных коэффициентов модели (коэффициентов регрессии), оценке их значимости и степени адекватности модели.