Функциональные ряды

4.1 Понятие функционального ряда. Область сходимости Определение 1. Ряд, вида

, (1)

Члены которого являются функциями переменного , называется функциональным рядом.

Если ряд (1) сходится при некотором , то точка называется точкой сходимости ряда. Множество всех точек сходимости ряда образует область сходимости ряда. В общем случае область сходимости может быть весьма сложной и состоять из совокупности интервалов. Определение области сходимости можно проводить применяя какой либо признак сходимости знакоположительных рядов, например, признак Даламбера или радикальный признак Коши к ряду, составленному из абсолютных величин членов ряда (1). В интервалах сходимости функциональный ряд (1) сходится абсолютно. Чтобы исследовать сходимость на концах интервалов сходимости, следует подставить в ряд вместо значения концевых точек интервалов и исследовать сходимость получившихся числовых рядов.

Пример 1. Найти область сходимости ряда .

Решение. При любом фиксированном получаем обобщенный гармонический ряд вида . Этот ряд сходится, если . То есть, областью сходимости ряда является интервал . В точке ряд принимает вид: . Это расходящийся гармонический ряд. Итак, окончательно, областью сходимости заданного ряда служит интервал .

Пример 2. Исследовать сходимость ряда .

Решение. Прежде всего, заметим, что ряд расходится, если , так как в этом случае , то есть не выполняется необходимый признак сходимости. Пусть . Применяя признак Даламбера к ряду, составленному из абсолютных величин членов данного ряда, находим, что этот ряд сходится, если

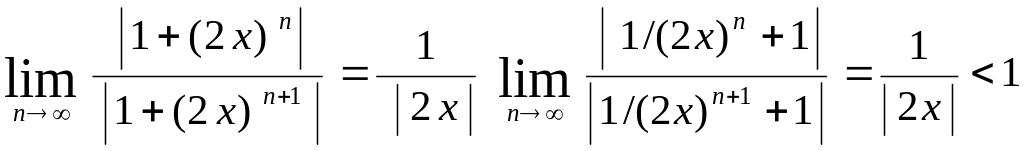
то есть при . Таким образом, ряд абсолютно сходится в интервалах и , и расходится вне этих интервалов.

4.2 Равномерная (правильная) сходимость функционального ряда

Пусть сумма ряда (1).

Определение 2. Функциональный ряд называется равномерно (правильно) сходящимся в некотором интервале , если для любого найдется такой номер , что для всех и всех выполняется неравенство

(2)

Можно сказать, что равномерная сходимость означает, что ряд сходится к своей сумме одинаково быстро при любом . Особое значение равномерно сходящиеся ряды имеют в связи с тем, что на них переносятся многие свойства конечных сумм. Это следует из теорем:

Теорема 1. Если члены равномерно сходящегося ряда являются непрерывными в интервале функциями переменного , то его сумма также является непрерывной в этом интервале функцией.

Доказательство. ►Чтобы доказать непрерывность функции в точке , нужно показать, что найдется такая точка , что разность будет меньше любого наперед заданного числа . Исходя из тождества

,

где я частичная сумма ряда, составим неравенство

. (3)

Пусть произвольное сколь угодно малое число. Выберем настолько близким к чтобы одновременно выполнялись неравенства

, , .

Справедливость первого и второго неравенств вытекает из равномерной сходимости ряда. Справедливость третьего следует из непрерывности конечных сумм непрерывных функций. Но тогда из (3) немедленно следует

, (4)

что и требовалось доказать. ◄

Теорема 2. Если ряд сходится к равномерно и его члены интегрируемы в интервале то сумма ряда также интегрируема в интервале , причем

. (5)

Доказательство. ►В силу равномерной сходимости ряда для любого найдется такой номер , что для всех имеет место неравенство (2) при любом . Но тогда

, (6)

а это означает, что последовательность частичных сумм ряда стремится к числу , что и требовалось доказать. ◄

Теорема 3. Пусть ряд сходится к в интервале и его члены непрерывно дифференцируемы в этом интервале. Тогда, если ряд

, (7)

составленный из производных членов исходного ряда, сходится равномерно в интервале , то сумма ряда дифференцируема, причем в каждой точке справедливо равенство

. (8)

Доказательство. ►Обозначим сумму ряда (7) . В силу предыдущей теоремы имеем равенство

или

.

Дифференцирование средней и правой частей этого равенства дает , ч.т.д. ◄

На практике, для установления равномерной сходимости функционального ряда, удобно применять признак Вейерштрасса:

Теорема 4 (Признак равномерной сходимости Вейерштрасса) Функциональный ряд сходится равномерно в интервале , если существует такой сходящийся знакоположительный ряд , что во всех точках интервала выполняются неравенства .

Доказательство. ►Согласно признаку сравнения ряд сходится в интервале абсолютно. Пусть его сумма. Тогда для -го остатка ряда можем записать

. (9)

Так как числовой ряд сходится, то для любого можно найти такой номер , что . Но тогда, в силу (9), неравенство будет иметь место при любом из интервала , что и доказывает равномерную сходимость ряда .◄

Пример 3. Показать, что ряд равномерно сходится на всей числовой оси.

Решение. Преобразуем общий член ряда воспользовавшись неравенством , которое выполняется для любых действительных чисел , :

,

откуда, при , следует, что

.

Так как неравенство выполняется для всех , а ряд сходится, то исходный ряд равномерно сходится на всей числовой оси.

Пример 4. Найти сумму ряда .

Указание: Воспользоваться формулой (см. формулу (32))

Решение. Пусть сумма ряда, то есть

.

Так как в области сходимости степенной ряд можно почленно дифференцировать, то

Согласно формуле (32), , так что:

.

Но тогда

.

Лекция 5.