29. Эффект Комптона, его объяснение из законов сохранения энергии и импульса. Энергия фотона и импульс фотона.

Эффектом Комптона называется упругое рассеяние коротковолнового электромаг­нитного излучения (рентгеновского и -излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны.

О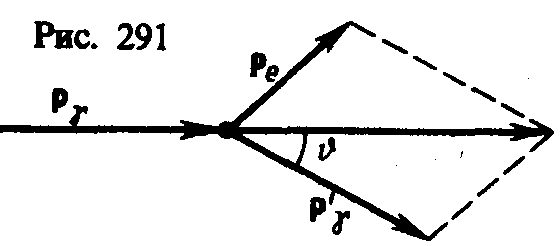бъяснение эффекта Комптона дано на основе квантовых представлений о природе света. Если считать, как это делает квантовая теория, что излучение имеет кор­пускулярную природу, т. е. представляет собой поток фотонов, то эффект Комп­тона — результат упругого столкновения рентгеновских фотонов со свободными элек­тронами вещества (для легких атомов электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными). В процессе этого столкновения фотон переда­ет электрону часть своих энергии и импульса в соответствии с законами их сохранения.

Рассмотрим упругое столкновение двух частиц (рис. 291) — налетающего фотона, обладающего импульсом p_ = h/c и энергией _=h, с покоящимся свободным электро­ном (энергия покоя W₀=m₀c²; т₀—масса покоя электрона). Фотон, столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения. При каждом столкновении выполняются законы со­хранения энергии и импульса. Согласно закону сохранения энергии, (206.2)а согласно закону сохранения импульса, (206.3) где W₀=m₀c² — энергия электрона до столкновения, _=h — энергия налетающего фотона, W=— энергия электрона после столкновения (используется релятивистская формула, так как скорость электрона отдачи в общем случае значитель­на), — энергия рассеянного фотона(h= 6,625×10–34 ). Подставив в выражение (206.2) значения величин и представив (206.3) в соответствии с рис. 291, получим(206.4) (206.5) Решая уравнения (206.4) и (206.5) совместно, получимПоскольку  = c/,  ' = c/' и  = ' – , получим(206.6)Выражение (206.6) есть не что иное, как полученная экспериментально Комптоном формула (206.1). Подстановка в нее значений h, m₀ и с дает комптоновскую длину волны электрона _C = h/(m₀c) = 2,426 пм.

30. Волна вероятности. Опыт Джермера и Дэвиссона. Волна де Бройля. Корпускулярно-волновой дуализм.

Волна при встрече с кристаллической решеткой дробится на отдельные пучки, которые уже не собираются вместе. А электрон не дробится ни при каких условиях и всегда обнаруживается как целое. Решение было найдено М. Борном, который воспользовался идеей Эйнштейна о том, что объединение волновых и корпускулярных свойств света возможно в принципе, если истолковывать квадрат амплитуды электромагнитной волны как вероятность обнаружения фотонов. Теория Борна состояла в следующем: квадрат амплитуды волны, связанной с движением электронов и других частиц, пропорционален вероятности обнаружения в этом месте частицы. Таким образом, квантово-механические волны имеют мало общего с обычными классическими волнами. Это волны вероятности.

Французский ученый Луи де Бройль (1892—1987), осознавая существующую в природе симметрию и развивая представления о двойственной корпускулярно-волновой приро­де света, выдвинул в 1923 г. гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.

Корпускулярно-волновой дуализм — теория в квантовой механике, гласящая, что в зависимости от системы отсчета поток фотонов можно рассматривать и как поток частиц (корпускул), и как волну. В частности, свет — это и корпускулы (фотоны), и электромагнитные волны.

Итак, согласно де Бройлю, с каждым микрообъектом связываются, с одной сторо­ны, корпускулярные характеристики — энергия Е и импульс p, а с другой — волновые характеристики — частота  и длина волны . Количественные соотношения, связыва­ющие корпускулярные и волновые свойства частиц, такие же, как для фотонов:

(213.1)

Смелость гипотезы де Бройля заключалась именно в том, что соотношение (213.1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля:

(213.2)

Это соотношение справедливо для любой частицы с импульсом р.

Во́лны де Бро́йля — волны, связанные с любой микрочастицей и отражающие их квантовую природу

Вскоре гипотеза де Бройля была подтверждена экспериментально. В 1927 г. амери­канские физики К. Дэвиссон (1881—1958) и Л. Джермер (1896—1971) обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки — кри­сталла никеля, — дает отчетливую дифракционную картину.