Записываем операторное уравнение

(Tp² + p)Y(p) = kX(p)

и передаточную функцию системы:

.

Полиномы числителя и знаменателя имеют вид:

.

Характеристическое уравнение разомкнутой системы D(p) = 0, то есть,

.

Корни этого характеристического уравнения действительные:

.

Пример 5.2.

Используя дифференциальное уравнение предыдущего примера, найти характеристическое уравнение и его корни для замкнутой системы.

Подставляя передаточную функцию разомкнутой системы в формулу (5.6), получаем характеристическое уравнение замкнутой системы:

.

Его корни:

Они могут быть как действительными (4 k T < 1), так и комплексными

(4 k T > 1) .

5.2. Критерий Гурвица. Устойчивость системы по Гурвицу выясняется с помощью характеристического уравнения. Составляется специальный определитель – определитель Гурвица. Правило следующее.

Намечают nстрок иnстолбцов (n– степень характеристического уравнения). В первый строке ставят все нечетные коэффициенты:a₁,a₃,a₅. По главной диагонали, начиная с коэффициентаa₁, слева-вниз-направо располагают последовательно все остальные коэффициенты. Столбцы, начиная с главной диагонали, заполняются вверх по нарастающим индексам, вниз - по убывающим. Все коэффициенты с индексами ниже нуля и выше степени уравнения, заменяют нулями.

Определители Гурвица 5-го, 4-го, 3-го и 2-го порядков выглядят следующим образом.

n = 5 n = 4 n = 3 n = 2

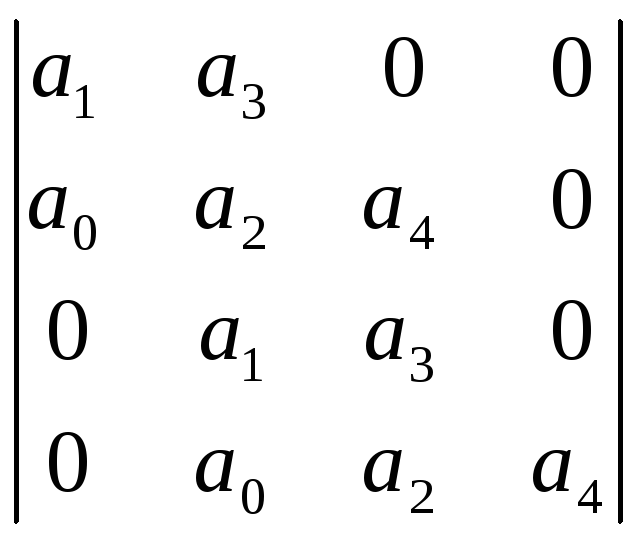
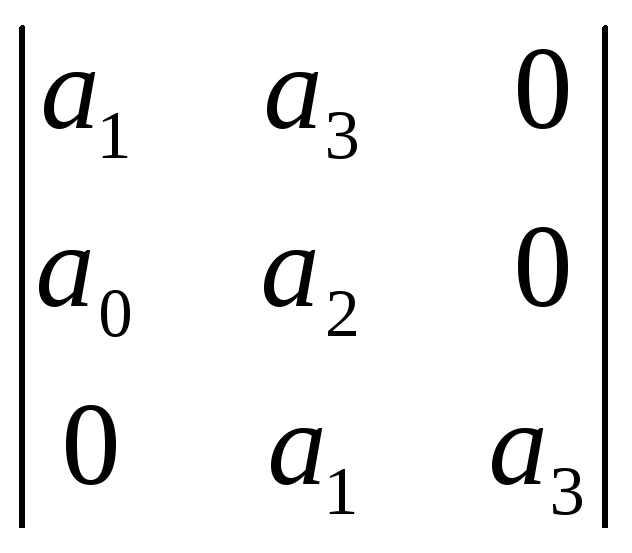
Для устойчивости системы необходимо, чтобы все коэффициенты характеристического уравнения и все определители были положительными.

Получим условия устойчивости для конкретных уравнений.

1. Характеристическое уравнение 2-й степени:

a₀p²+a₁p+a₂ = 0 .

Ему соответствует определитель Гурвица 2-го порядка:

= a₁a₂ - a₀ · 0 = a₁a₂. ₂ = a₁a₂ .

Условие устойчивости: a₀, a₁, a₂ > 0; ₂ > 0, т.е. a₁a₂ > 0.

2. Характеристическое уравнение 3-й степени:

a₀p³ + a₁p² + a₂p + a₃ = 0.

Ему соответствует определитель Гурвица 3-го порядка:

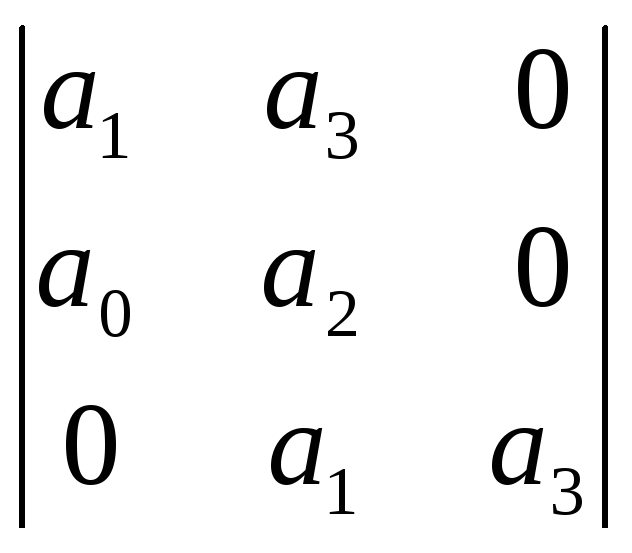= a₁(a₂a₃ - a₁0) - a₃(a₀a₃ - 0·0)+0(a₀a₁ - a₂·0).

Δ₃ = a₁a₂a₃ - a₀a²₃.

Условие устойчивости: a₀, a₁, a₂, a₃ > 0; Δ₃ > 0, или, сокращая на a₃, a₁a₂ – a₀a₃ > 0.

3. Характеристическое уравнение 4-й степени:

a₀p⁴ + a₁p³ + a₂p² + a₃p + a₄ = 0 .

Ему соответствует определитель Гурвица 4-го порядка:

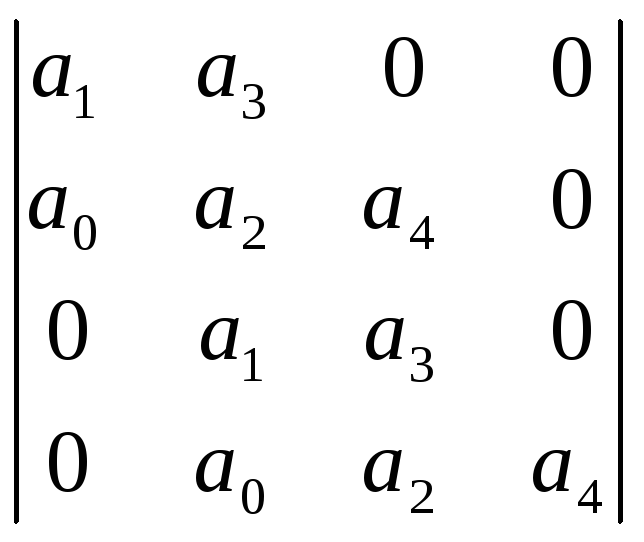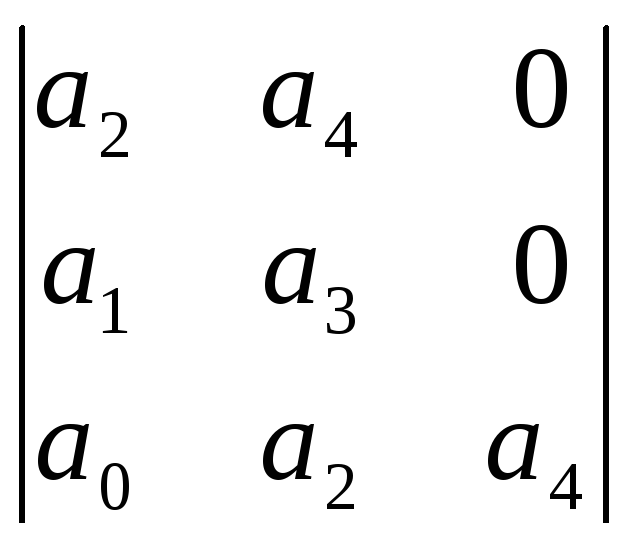= а₁ - а₃ 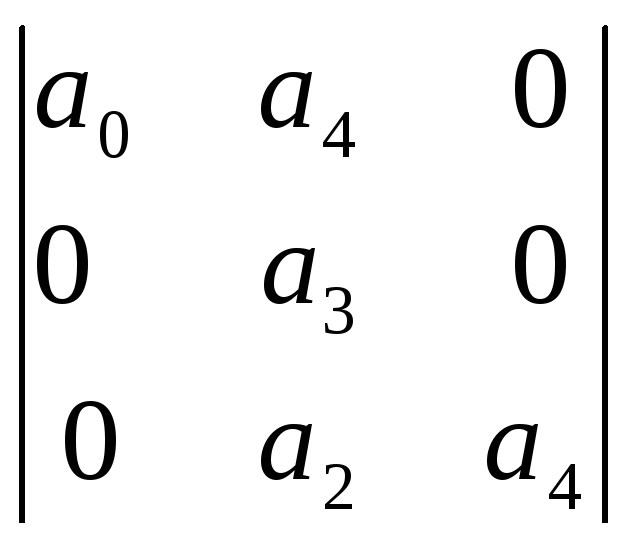+ 0 – 0 .

Δ₄ = a₁a₂a₃a₄ – a²₁a²₄ – a₀a²₃a₄ .

Условие устойчивости: a₀, a₁, a₂, a₃, a₄ > 0, Δ₄ > 0, или сокращая на a₄, a₁a₂a₃ - a²₁a₄ - a₀a²₃ > 0 .

4. Характеристическое уравнение 5-й степени:

a₀p⁵ + a₁p⁴ + a₂p³ + a₃p² + a₄p + a₅ = 0 .

Опуская процедуру вычисления определителя, выпишем сразу условие устойчивости:

a₀, a₁, a₂, a₃, a₄, a₅ > 0,

(a₁a₂ – a₀a₃)(a₃a₄ – a₂a₅) – (a₁a₄ – a₀a₅)² > 0 .

Можно составлять определители Гурвица и для характеристических уравнений более высокой степени, получая соответствующие условия устойчивости. Однако, объем вычислений нарастает с увеличением степени характеристического уравнения, поэтому считается приемлемым пользоваться критерием Гурвица для характеристических уравнений степени не выше пятой.

Определитель Гурвица позволяет найти коэффициент усиления на границе устойчивости. Коэффициент усиления – это свободный член характеристического уравнения, его индекс равен степени уравнения. Границей устойчивости будет условие Δ= 0. Откуда и вычисляется коэффициент усиления.

Пример 5.3.

Дана система, характеристическое уравнение которой имеет вид :

T₁ T₁T₂T₃p³ + (T₁T₂ + T₁T₃ + T₂T₃)p² + (T₁ + T₂ + T₃)p + 1 + k = 0 .

Выяснить, будет ли система устойчивой, если T₁ = 1, T₂ = 2, T₃ = 3, k = 19 ? Каким должен быть коэффициент усиления на границе устойчивости?

Записываем характеристическое уравнение 3-й степени в общем виде, сопоставляем его с заданным и заключаем:

a₀= T₁T₂T₃ , a₂= T₁+T₂+T_{3 ,}

a₁= T₁T₂+T₁T₃+T₂T₃ , a₃=1+k .

Все коэффициенты больше нуля, но надо проверить, будет ли определитель Гурвица больше нуля. Подставив числа в неравенство a₁a₂ - a₀a₃ > 0, обнаруживаем, что оно не выполняется: 66 - 120 < 0. Определитель оказался отрицательным. Следовательно, система неустойчива.

На границе устойчивости a₁a₂ - a₀a₃ = 0. Подставляя числа, имеем: 11·6 = 6 (1 + k). Коэффициент усиления на границе устойчивости k = 10.

П

ример 5.4.

Выяснить, будет ли устойчивой система с характеристическим уравнением

5p⁴ + p + 2 = 0 .

Сопоставив данное уравнение с его общим видом, получаем:

a₀ = 5, a₁ = a₂ = 0, a₃ = 1, a₄ = 2.

По условию устойчивости a₁a₂a₃ – a₁²a₄ – a₀a₃² > 0. Это не выполняется:

-5∙1² < 0. Система неустойчива, хотя все коэффициенты положительные.

П

ример 5.5.

Звенья, передаточные функции которых

и,

соединяются последовательно. Выяснить, будет ли такая система устойчивой? Какую величину имеет постоянная времени T₀ на границе устойчивости замкнутой системы?

Находим передаточную функцию разомкнутой системы

.

Ее знаменатель, приравненный к нулю, есть характеристическое уравнение. После сокращения на T₀ характеристическое уравнение выглядит так:

T₁²p³ + T₂p² + p = 0 .

Сопоставляя с записью характеристического уравнения в общем виде, делаем вывод:

a₀ = T₁², a₁ = T₂, a₂ = 1, a₃ = 0.

Для уравнения 3-й степени условия устойчивости требуют, чтобы

a₀, a₁, a₂, a₃ > 0 , a₁a₂ - a₀a₃ > 0 .

Это соблюдается: T₁² , T₂ , 1 > 0 , T₂ – 0 ∙ T₁² > 0 . Следовательно, разомкнутая система устойчива.

Составим характеристическое уравнение замкнутой системы. Это будет сумма полиномов числителя и знаменателя, приравненная к нулю:

T₀ T₁²p³ + T₀T₂p² + T₀(k₁k₂ + 1)p + k₁k₂ = 0.

Выписываем коэффициенты:

a₀ = T₀T₁², a₁ = T₀ T₂ , a₂ = T₀(k₁k₂ + 1) , a₃ = k₁k₂ .

Выясняем устойчивость:

T₀T₁², T₀T₂ , T₀(k₁k₂ + 1) , k₁k₂ > 0 .

Замкнутая система будет устойчивой, если

T₀T₂ (k₁k₂ + 1) - k₁k₂ T₁² > 0 .

На границе устойчивости определитель равен нулю, из чего заключаем:

.