Дискретное преобразование Фурье

Пара непрерывного преобразования Фурье имеет вид:

Выражение для прямого преобразования имеет вид:

, k=0…N-1

для обратного:

, n=0…N-1

Выражение для ДПФ ставит в соответствие N отсчетам сигнала s(n), n=0…N-1, в общем случае комплексного, N отсчетов спектра S(k), k=0…N-1.

В непрерывном так и в дискретном случае, в выражении для обратного преобразования имеется нормировочный коэффициент. В случае интеграла Фурье это  , в случае обратного преобразования это . Можно отметить, что в случае непрерывного преобразования нормировочный коэффициент призван корректно отображать масштабирование сигнала во времени в частотную область и наоборот.

Другими словами, если последовательно рассчитать спектр некоторого сигнала, а после взять обратное преобразование Фурье, то результат обратного преобразования должен полностью совпадать с исходным сигналом. Нормировочный коэффициент уменьшает амплитуду сигнала на выходе обратного преобразования для того чтобы она совпадала с амплитудой исходного сигнала.

Быстрое преобразование Фурье

Быстрое преобразование Фурье преследует следующие цели:

• получение спектра частот анализируемого сигнала дискретного по времени;

• уменьшение вычислительных ресурсов по сравнению с классическим дискретным преобразованием Фурье (ДПФ).

Для дискретного преобразования Фурье (ДПФ) справедливы все свойства интегральных преобразований Фурье, однако при этом следует учитывать периодичность дискретных функций и спектров.

Для вычисления каждой гармоники ДПФ необходимо N операций комплексного умножения и сложения и соответственно N² операций на полное выполнение ДПФ. При больших объемах массивов данных это может приводить к существенным временным затратам. Ускорение вычислений достигается при использовании быстрого преобразования Фурье.

Как пример ДПФ возьмем сигнал, который состоит из 8 отсчетов во временной области, которые будут преобразовываться в восемь частотных составляющих в частотной области. При числе отсчетов N=8 уравнение будет выглядеть как:

, k=0,1,…,7

Каждое слагаемое, представляющее собой произведение комплексных чисел, складывается с другими слагаемыми. Поскольку k принимает значения от 0 до 7, т.е. вычисляется восемь отсчетов ДПФ, всего потребуется 8*8 = 64 умножения и 8*7 = 56 комплексных сложений.

ДПФ неэффективно, так как не учтены свойства симметрии и периодичности поворачивающего множителя .

Свойство симметрии:

Свойство периодичности:

Указанные два свойства используются для повышения эффективности вычислений ДПФ с помощью различных алгоритмов БПФ.

Поскольку является периодической функцией с ограниченным числом известных значений, можно ускорить вычисление ДПФ, если сократить количество вычислений этой функции. Для этого разобьем ДПФ на два ряда: один – по четным, а второй – по нечетным членам последовательности x(n), как показано ниже:

Можно увеличить число идентичных слагаемых с помощью следующего действия:

Так как поворачивающий множитель не зависит от индекса r, его можно вынести за знак суммы, в результате получим:

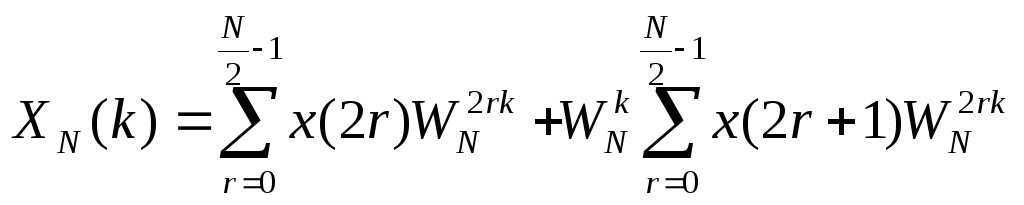
Применяя свойства поворачивающего множителя и, получаем окончательное выражение БПФ:

Данный метод позволяет снизить трудоемкость ДПФ до порядка (N/2)².

Вышеприведённые способы оптимизации, служат основой для ряда других быстрых алгоритмов вычисления ДПФ. Наиболее широко распространенным из них является вычисление БПФ по основанию 2 или алгоритм Кули-Тьюка. Суть метода заключается в том, что после разбиения последовательности отсчетов сигнала на два множества (четные и нечетные отсчеты), каждое из полученных множеств также разделяется (прореживаются) на две части вплоть до двухточечных наборов.

Вычисление БПФ по основанию 2 значительно проще, чем вычисление ДПФ, так как необходимо вычислять только 2-точечные ДПФ. Однако вычисляемые поворачивающие множители будут различными на каждом этапе прореживания.