Федеральное агентство по образованию

Санкт-Петербургский государственный

электротехнический университет «ЛЭТИ»

Кафедра ВТ

Реферат № 3

по дисциплине

«Алгоритмы и процессоры цифровой обработки сигналов» на тему

«Линейные дискретные системы с постоянными параметрами»

Выполнил:

Группа:

Санкт-Петербург

2013

Оглавление

Линейные разностные уравнения 3

Импульсная характеристика дискретной ЛПП-системы 4

1.Условие физической реализуемости 5

2.Условие устойчивости системы 6

Частотная характеристика дискретной ЛПП-системы 7

Z-преобразование 9

Примеры ЛПП-систем 10

ЛПП-система – линейная система с постоянными параметрами.

Линейные разностные уравнения

Линейные системы можно описать с помощью разностных уравнений. По структуре эти уравнения напоминают дифференциальные уравнения непрерывных систем. Сначала рассмотрим понятия о конечных разностях для дискретной функции х(iТ_n). Нулевой конечной разностью называется само значение дискретной функции и обозначается через Δ₀ x(iT_n) = x(iT_n)

Это понятие аналогично нулевой производной непрерывной функции.

Первой конечной разностью называется выражение Δ₁ x(iT_n) = (iT_n) - x[(i-1)T_n], где x[(i-1)T_n] - значение функции в предшествующем периоде следования. Δ₁ x(iT_n) определяет приращение функции на период и по смыслу близко к понятию первой производной непрерывных функций.

Вторая разность равна разности первых разностей:

Δ₂ x(iT_n) = Δ₁ - Δ₁ x[(i-1)T_n] = x(iT_n)-2x[(i-1)T_n]+ x[(i-2)T_n].

Третья разность равна разности вторых разностей:

Δ₃ x(iT_n) = Δ₂ x(iT_n) - Δ₂ x[(i-1)T_n] = x(iT_n) - 3x[(i-1)T_n] + 3x[(i-2)T_n] - 3x[(i-2)T_n]- x[(i-3)T_n],

и, в общем случае, разность k-го порядка

Δ_k x(iT_n) = Δ_k-1 x(iT_n) - Δ_k-1 x[(i-1)T_n].

Этой разности можно сопоставить понятие k-й производной непрерывной функции. k-ю разность можно выразить через значения дискретной функции следующим образом:

Δ_k x(iT_n) = x(iT_n) - kx[(i-1)T_n] + C²_k x[(i-2)T_n] - C³_k x[(i-3)T_n] + + ... - C^k-1_k x[(i-k+1)T_n] + x[(i-k)T_n],

где С1k - число сочетаний из k по r.

Разностное уравнение дискретной системы устанавливает соответствие между входным и выходным дискретными процессами и их разностями. Линейным системам соответствует линейное соотношение между этими переменными, которое имеет вид:

Данное уравнение называется линейным конечно-разностным уравнением и по своей структуре соответствует линейному дифференциальному уравнению. Коэффициенты   и  определяются параметрами системы, в том числе они зависят от периода повторения T_n. Если параметры системы не зависят от времени, то коэффициенты уравнения будут постоянными и система называется стационарной.

Максимальный порядок п разности выходного процесса называется порядком уравнения или порядком дискретной системы. Решение разностного уравнения можно записать в виде суммы

y(iT_n) = y_n(iT_n)+ y_x(iT_n),

которая состоит из дискретного переходного процесса y_n(iT_n) и вынужденного процесса y_x(iT_n).

Переходный процесс находится из решения однородного уравнения

при начальных условиях у(0), Δ₁ y(0), ... , Δ_n-1 y(0) для момента включения системы t = 0. Вынужденный процесс y_x(iT_n) является частным решением при нулевых начальных условиях и заданном воздействии х(iT_n).

Импульсная характеристика дискретной ЛПП-системы

В теории ЛПП-систем важное место занимает сигнал «единичный импульс»:

Любой дискретный сигнал может быть представлен в виде свертки его самого же с единичным импульсом

.

Подадим на вход дискретной ЛПП-системы тестовый сигнал “единичный импульс” и получим его отклик.

h(n)=A[u₀(n)], -∞ < n < +∞

Этот отклик будет каким-то определенной для данной ЛПП-системы Данная функция определяет ЛПП-систему, поэтому ее называют импульсной характеристикой дискретной ЛПП-системы. Если известна импульсная характеристика, то при всяком известном входном сигнале возможно рассчитать выходной сигнал по формуле :

(1)

Соотношения такого типа называют дискретными свертками. Можно сказать, что выход дискретной ЛПП-системы представляет собой дискретную свертку входного сигнала с импульсной характеристикой системы.

Многие дискретные ЛПП-системы, в частности реализуемые в виде цифровых устройств, должны удовлетворять следующим двум важным условиям.

1. Условие физической реализуемости

Выход y(n) зависит только от x(m), m≤n, т.е. не зависит от будущих значений входного сигнала. Это условие выполняется, если

В этом случае возможно переписать формулу выходного сигнала (1):

Т.е. каждый отсчет выходного сигнала определяется взвешенной суммой текущего и предыдущих отсчетов входного сигнала. При бесконечном суммировании возможно получить бесконечные значения выходного сигнала. Из-за этого нужно наложить дополнительные ограничения на импульсную характеристику.

2. Условие устойчивости системы

Система устойчива, если из условия следует . Необходимым и достаточным условием устойчивости дискретной ЛПП-системы является следующее ограничение на импульсную характеристику:

, которое может быть выполнено при достаточно быстром убывании импульсной характеристикой при больших по модулю значениях индекса m.

Частотная характеристика дискретной ЛПП-системы

Дискретная ЛПП-система однозначно определяется своей импульсной характеристикой h(n), поскольку она дает возможность предсказать выход системы при любом вход. Частотная характеристика ЛПП-системы позволяет описать свойства ЛПП-системы.

Подадим на вход системы дискретизированную комплексную синусоиду частоты :

,

Подставив это в формулу (1), и получим, что выходной сигнал может быть записан в виде:

где комплексный коэффициент есть преобразование Фурье для импульсной характеристики:

Дискретная синусоида остается синусоидой той же частоты . Действие комплексного коэффициента приводит лишь к изменению амплитуды синусоиды в раз, и фазовой задержке на величину

радиан.

Произвольный дискретный сигнал x(n) может быть представлен в виде преобразования Фурье:

,

фактически представляющего собой суперпозицию комплексных синусоид всех частот из интервала [-π, π]. - частотный спектр сигнала:

Подадим сигнал x(n) на вход ЛПП-системы. Учитывая свойство линейности системы и соотношения (10)-(11), выходной сигнал можно представить в виде:

Отсюда можно сделать 2 вывода:

1. Зная функцию 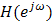на интервале частот [-π, π], мы имеем возможность рассчитывать выход системы при любом известном входе. Следовательно, как и импульсная характеристика h(n), функция тоже определяет дискретную ЛПП-систему.

2. Функция определяет закон преобразования частотного спектра входного сигнала в частотный спектр сигнала на выходе дискретной ЛПП-системы:

Учитывая все это, функцию , определяемую соотношением , называют частотной характеристикой дискретной ЛПП-системы.

Z-преобразование

Z-преобразование представляет собой разложение функций в ряды степенных полиномов по z.

Произвольной непрерывной функции s(t), равномерно дискретизированной и отображенной отсчетами , равно как и непосредственно дискретной функции, можно поставить в однозначное соответствие степенной полином по z, последовательными коэффициентами которого являются значения

s_k:

где - произвольная комплексная переменная. В показательной форме где r = |z| = , ).

В каузальных системах значения импульсного отклика систем существуют при k ≥ 0 и уравнение действует в одностороннем варианте:

H(z) =h_k z^k.

В общем случае, z-преобразование – это степенной ряд с бесконечным количеством членов, поэтому он может сходиться не для всего пространства значений z. Область z, в которой z-преобразование сходится и значения S(z) конечны, называют областью сходимости.

Z-образы с положительными степенями z соответствуют каузальным (физически реализуемым) процессам и системам, которые работают в реальном масштабе времени с текущими и «прошлыми» значениями сигналов. При обработке информации на ЭВМ каузальность сигналов не относится к числу ограничений и возможно использование отрицательных степеней z, соответствующих отсчетам сигналов «вперед». Последнее применяется, например, при синтезе симметричных операторов фильтров, что позволяет производить обработку информации без внесения в сигнал фазовых искажений. При использовании символики z^-1 «прошлым» значениям соответствуют значения с отрицательными степенями z, «будущим» – с положительными.

Основное достоинство z-преобразований заключается в простоте математических операций со степенными полиномами, что имеет немаловажное значение при расчетах цифровых фильтров и в спектральном анализе.

Примеры ЛПП-систем

Сумматор:

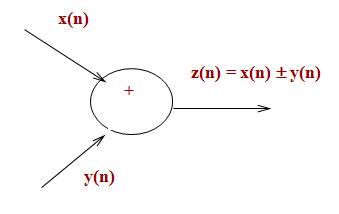
Усилитель:

Накопитель: