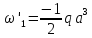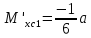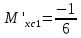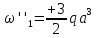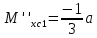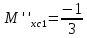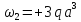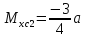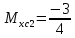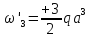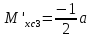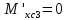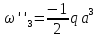2 вариант схема 35
.docx
1.3 Расчёт бруса при изгибе
1.3.1 Условие задачи
Для двухопорной
балки (схема 35), выполненной из стали
Ст3, имеющей постоянное по длине
прямоугольное сечение (h/b=2), в общем виде
определить прогибы методом Мора в
сечении С и способом Верещагина в сечении
D и угол поворота на правой опоре. Из
условий прочности и жесткости (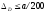 )
определить размеры поперечного сечения
балки. Используя вид эпюры Mx
и вычисленные значения прогибов и угла
поворота при найденных размерах
поперечного сечения, показать для балки
характер изогнутой оси бруса с указанием
перемещений сечений C
и D
и угла поворота на правой опоре.
)
определить размеры поперечного сечения
балки. Используя вид эпюры Mx
и вычисленные значения прогибов и угла
поворота при найденных размерах
поперечного сечения, показать для балки
характер изогнутой оси бруса с указанием
перемещений сечений C
и D
и угла поворота на правой опоре.
1.3.2 Краткие теоретические сведения
Перемещение сечений (прогибы или углы поворота) при изгибе бруса определяем методом Мора в соответствии с которым
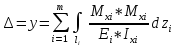
Перемещение сечений (прогибы или углы поворота) при изгибе бруса определяем способом Верещагина в соответствии с которым
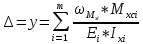
1.3.3 Исходные данные
Схема 35; q
= 0,02 МН/м; a
= 1 м; P
= qa;
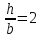 ;
материал Ст 3: nт
= 1,5;
;
материал Ст 3: nт
= 1,5;
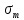 = 240 МПа;
= 240 МПа;
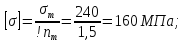 E
= 2,1*105
МПа
E
= 2,1*105
МПа
Определить: 1) yC
= ?, yD
= ?,
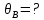
2) из условия прочности и жёсткости b = ?, h = 2b = ?
3) построить упругую линию y = y(z)
1.3.4 Решение задачи
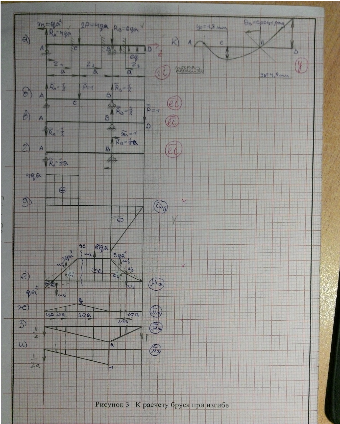
1.3.4.1 Для определения перемещений выбираем соответствующее единичное состояние (рис. 3 б, в, г)
1.3.4.2 Из условия равновесия определяем реакции в опорах для грузового состояния (рис. 3 а)
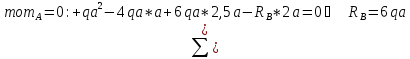
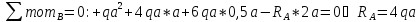
Проверка:
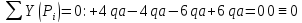
Аналогично определяем реакции для единичных состояний
ec:
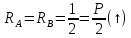 (рис. 3б)
(рис. 3б)
ec:
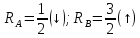 (рис. 3в)
(рис. 3в)
ec:
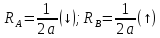 (рис. 3г)
(рис. 3г)
1.3.4.3 Запишем выражения для изгибающих моментов для грузового и единичного состояний по силовым участкам
1
СУ
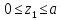 :
:
гс:
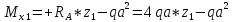
ec:
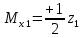
ec:
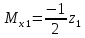
ec:
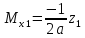
2
СУ
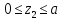 :
:
гс:
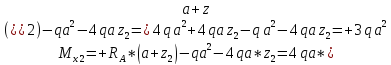
ec:

ec:
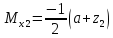
ec:
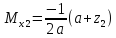
3
СУ
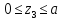 :
:
гс:
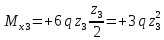
ec:
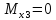
ec:
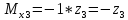
ec:
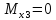
1.3.4.4 Строим эпюры и аналитические выражения перерезывающей силы и изгибающего момента в грузовом и единичном состоянии по участкам (Рис. 3е, ж, з, и). По эпюре Мх определяем опасное сечение
1.3.4.5 Определяем вертикальное перемещение сечения С методом Мора при EIx = const
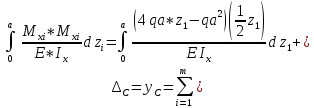

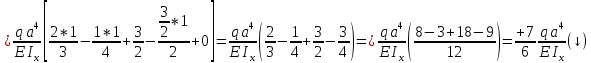
1.3.4.6 Определим вертикальное перемещение сечения D и угол поворота сечения B используя способ Верещагина
Дополнительные вычисления:
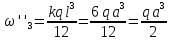
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
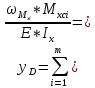
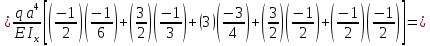
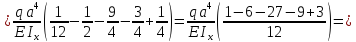
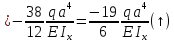
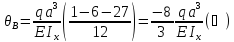
1.3.4.7
Определим размеры поперечного
прямоугольного сечения при
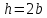 из условий прочности и жёсткости
из условий прочности и жёсткости
а) из условия прочности
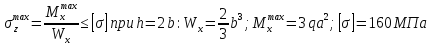
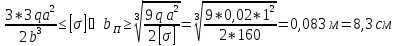
б) из условия жесткости

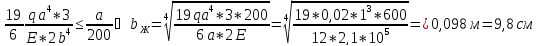
в) из двух размеров выбираем наибольший

h = 2b = 19,6 см
1.3.4.8 Определим перемещение сечений C и D и угол поворота сечения B для балки с поперечным сечением 9,8×19,6 см для которого
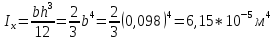
a) перемещение сечения С:
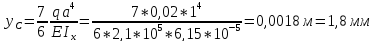
б) перемещение сечения D:
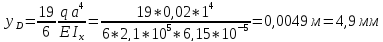
в) угол поворота сечения B:

1.3.4.9 Учитывая вид эпюры Mx и вычисленные перемещения на рисунке 3к покажем характер упругой оси балки
Ответ: b=9,8 см; h = 19,6 см