
- •1)Изгиб. Определения. Основные типы балок и опор. Правило знаков.
- •2)Формула Журавского. Условие прочности по касательным напряжениям.
- •3)Осевое растяжение (сжатие). Внутренние силы, напряженя, деформациию. Закон Гука. Условие прочности и жесткости.
- •4)Дифференциальные зависимости при изгибе. Правило контроля правильности построения эпюр.
- •5)Статически неопределимые задачи. Основные понятия и определения. Особенности статически неопределимых конструкций.
- •6)Нормальные напряжения при чистом изгибе. Условие прочности балок по нормальным напряжениям. Три типа задач при расчетах балок на прочность.
- •7)Дифференциальное уравнение прогнутой оси балки. Определение деформаций балки методом начальных параметров.
- •8)Геометрические характеристики сечений. Определение координат центров тяжести и моментов инерции сечения сложной формы.
- •9) Задачи курса «Сопротивления материалов». Объекты, изучаемые в курсе. Классификация внешних сил. Допущения относ. Свойств материала. Допущения относительно характера деформации.
- •10)Внутренние силы. Метод сечений. Общие и частные случаи нагружения.
- •11)Дифференциальные уравнения изогнутой оси балки. Определение деформаций балки методом непосредственного интегрирования.
- •12)Распространение касательных напряжений в балках прямоугольного и двутаврового профиля.
- •13) Экспериментальное изучение свойств материалов. Диаграмма растяжения. Коэффициенты запаса прочности. Определение допускаемых напряжений.
- •14)Геометрические характеристики сечений. Моменты инерции относительно параллельных осей.
- •15)Вычисление момента инерции при повороте осей. Главные оси инерции и главные моменты инерции.
- •16) Формула Эйлера для определения критической нагрузки сжатого стержня.
- •17) Предел применимости формулы Эйлера. Расчеты на устойчивость.
- •18) Сложное сопротивление. Изгиб с кручением брусьев. Условие прочности.
- •19) Внецентренное растяжение (сжатие) брусьев. Эпюра напряжений. Условие прочности.
- •20) Косой изгиб. Эпюра нормальных напряжений. Вычисление прогиба. Условие жесткости и прочности.
- •21)Кручение бруса круглого поперечного сечения. Определение напряжений и углов закручивания. Расчет на прочность и жесткость.
- •22)Практические расчеты на срез и смятие.
- •23)Внецентренное растяжение (сжатие) брусьев. Ядро сечения.
- •24)Основы напряженного состояния в точки. Главные площадки и главные напряжения. Прямая и обратные задачи. Линейное напряженное состояние.
- •25)Плоское напряженное состояние. Анализ формул.
- •26)Деформации при плоском напряженном состоянии. Обобщенный закон Гука.
- •27)Энергия деформации при изгибе. Интеграл Мора. Порядок решения задач методом Мора.
- •28)Энергия деформации при изгибе. Теорема Кастильяна.
- •29)Потенциальная энергия деформации. Гипотезы прочности.
- •30)Метод сил для расчета статически неопределимых систем.
- •Вопросы на экзамен по курсу «Сопротивление материалов»
16) Формула Эйлера для определения критической нагрузки сжатого стержня.

Определим величину силы F, при которой форма равновесия становится неустойчивой (минимальную величину силы, при которой становится неустойчивой). Вывод основуется на допущениях:
1) Напряжение в сечениях бруса не превышает предела пропорциональности (напряжение, до которого сохраняется закон Гука), т.е. материал работает в пределах упругости.
2) Деформации бруса равны по сравнению с его размерами, тогда можно применять диф-е ур-е изогнутой оси бруса.
d2W/dx2=M(x)/EImin; M(x)= –Fx;
d2W/dx2= –FW/EImin; W″+ +(F/EImin)W=0; k2=F/EImin; W(x)= Asinkx + Bcoskx;
1) при x=0:
W(0)=0; A∙0+B∙0=0; B=0.
2) при x=ℓ:
W(ℓ)=0: W(ℓ)=Asinkℓ=0; A≠0; sinkℓ=0; kℓ=πn; k=πn/ℓ. Приравнивая k к k2 получаем: n2π2/ℓ2 = F/EImin; F= n2π2 EImin /ℓ2; при n=1→Fmin=Fкр
Fкр=π2EImin/ℓ2 – формула Эйлера.
W(x)=Asinkx; Wmax при х-?:
W′x(x)=Akcoskx=0; coskx=0; kx= π/2; x=π/2k; Wmax=A∙1=f→A=f.
W(x)=fsinkx – закон изменения деформации стержня по длине бруса. Определим геометрический смысл n.
х (координата)=π/2k – координата max. прогиба.
x=π/2k={k=nπ/ℓ}=πℓ/2nπ=ℓ/2n;
xmax=ℓ/2n.
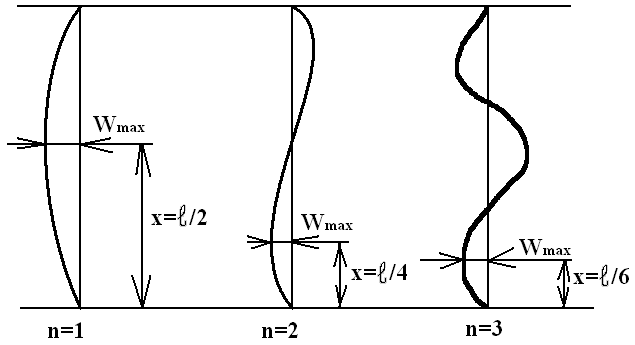
Для n=1: Fкр=x2EImin/ℓ2;
Для n=2: Fкр=4π2EImin/ℓ2;
Для n=3: Fкр=9π2EImin/ℓ2;
n показывает сколько полуволн укладывается на длине бруса при потере устойчивости под действием Fкр.

Iz=bh3/12; Iy=bh3/12; Iz >> Iy;
Iz – ось наибольшей жесткости. EIz – жесткость поперечного сечения бруса на изгиб. Iy – ось наименьшей жесткости. Плоскость xOz перпендикулярна оси наименьшей жесткости. При продольном изгибе бруса (потере его устойчивости) изогнутая ось лежит в плоскости перпендикулярной оси наименьшей жесткости. Ось y – нейтральная ось. Если для бруса Iz ≠ Iy, то всегда при потере устойчивости изогнутая ось лежит в плоскости перпендикулярной оси наименьшей жесткости, и в формулу Эйлера подставляем наименьший из моментов инерции. Рациональной формой поперечного сечения для сжатого длинного и тонкого бруса будет та, у которой моменты инерции Iz = Iy (обладающие центральной симметрией и имеющие момент инерции при наименьшей площади).

А1=А2; I1>>I2; 1 рациональней 2.
17) Предел применимости формулы Эйлера. Расчеты на устойчивость.
Критическое напряжение σкр – это напряжение, которое возникает в сжатом брусе при нагрузке F=Fкр.
σкр=Fкр/A=π2EImin/Aℓ2={Imin/A= i2min}=π2E/(ℓ/i)2 – для шарнирно опертого бруса.
λ пред ={предельная гибкость}= √(π2E/σпропорц) – зависит только от свойств материала.
λ ≥√(π2E/σпропорц); λ пред ≥ λ; При решении задачи на устойчивость надо делать проверку:
– посчитать λ для рассматриваемого бруса.
– сравнить с λпред, взятым из таблиц.
Если λ< λпред, то расчет ведут по формулам Ясинского, или только на сжатие в зависимости от величины λ.
Формула Ясинского: σкр=a-bλ. Формула Ясинского для конструкционных материалов; a и b получены экспериментальным путем, их берут из таблиц. σкр=π2E/λ2; При расчетах брусьев на сжатие, необходимо определить геометрическую характеристику λ из таблиц для рассматриваемого материала, выбрать величины из таблиц λ0 и λпред, и после этого определиться по каким формулам следует вести расчет на сжатие.
