4.1. Теплопроводность плоской стенки

Рассмотрим плоскую стенку, высота и ширина которой значительно больше её толщины. В этом случае такую стенку можно считать бесконечной (рис. 5). Тепло будет передаваться только в одном направлении – вдоль оси х. Если считать, что теплопроводность стенки величина постоянная, то уравнение теплопроводности в

Рис.5. Плоская стенка

этом случае можно записать в виде . (4.1) Решение (4.1) имеет вид , где С1 и С2 – постоянные. Для их определения нужно задать два граничных условия. а) граничные условия первого рода при х=0 ; при .

Получим два уравнения для определения С₁ и С₂

и ,

из которых найдём и . Таким образом,

. (4.2)

Количество тепла, проходящего через стенку, определим по закону Фурье.

. (4.3)

Разность температур называется температурным напором, а – термическим сопротивлением теплопроводности плоской стенки, м²град/Вт.

Из формулы (4.2) следует, что распределение температуры в плоской стенке представляет собой прямую линию, а из (4.3) следует, что плотность теплового потока через плоскую стенку не зависит от координаты х.

Рассмотрим теплопроводность многослойной плоской стенки, состоящей из n слоёв различной толщины из разных материалов с разной теплопроводностью . При стационарном тепловом режиме тепловой поток одинаков в каждом слое.

Рис.6. Многослойная плоская стенка

; ; ………………… . Из этих уравнений найдём температурные напоры в каждом слое.

;

;

……………….

.

Сложив уравнения, получим

.

откуда

.

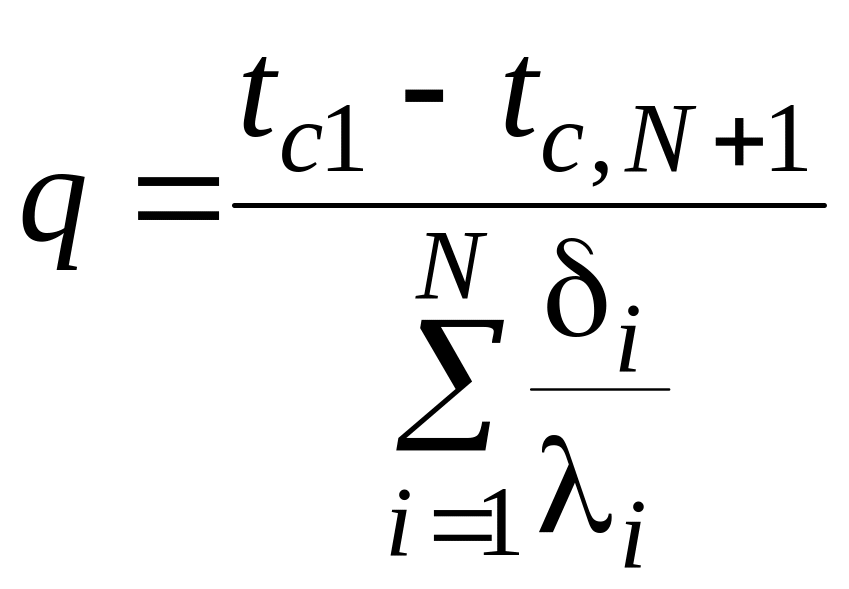б) граничные условия третьего рода

Рис. 7. Граничные условия третьего рода

Передача тепла от одной жидкости к другой через разделяющую их стенку называется теплопередачей. Расчётная схема приведена на рис.7. С одной стороны стенки находится жидкость с температурой , с другой стороны – жидкость с температурой . Примем для определённости, что > . Перенос тепла между жидкостями и стенкой рассчитывается по формуле Ньютона – Рихмана. Будем считать коэффициенты теплоотдачи постоянными и не завися-

щими от температуры. В соответствии с формулой Ньютона тепловой поток между жидкостью и левой стороной стенки определяется как

. (а)

В стационарных условиях этот же тепловой поток пройдёт через стенку и передастся к другой жидкости.

; (б)

. (в)

Найдём из (а) – (в) разности температур, сложим получившиеся выражения и найдём q.

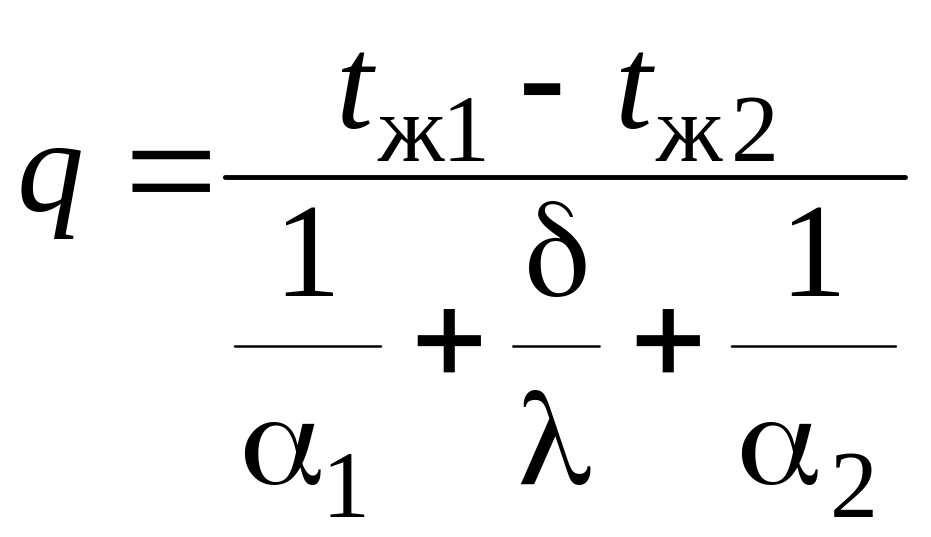. (4.4)

Обозначим

.

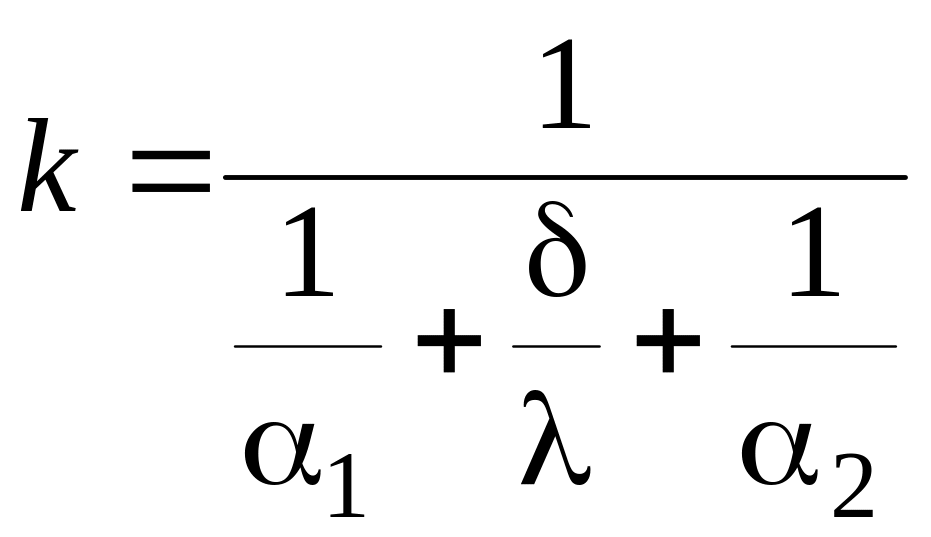Тогда (4.4) можно переписать в виде

.

Величина k называется коэффициентом теплопередачи и имеет ту же размерность, как и коэффициент теплоотдачи, Вт/м²К. Величина обратная k называется полным термическим сопротивлением теплопередачи

,

а отношение называется термическим сопротивлением теплоотдачи.

Общее термическое сопротивление равно сумме частных сопротивлений, поэтому для многослойной стенки полное термическое сопротивление можно записать в виде

и плотность теплового потока в случае многослойной стенки запишем в виде

.

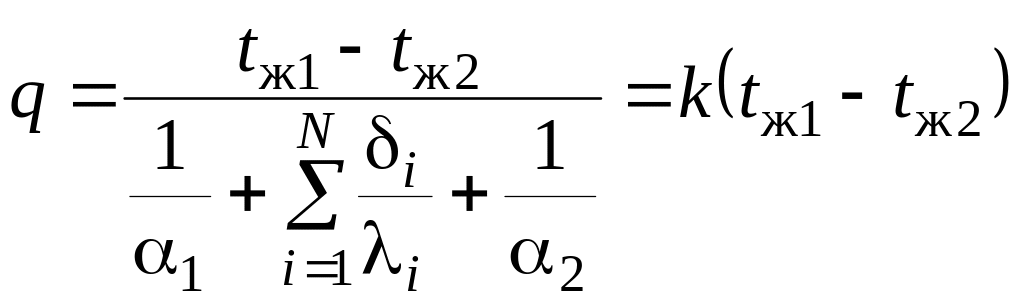Температуры на поверхностях стенки и найдём из (а) и (в)

;

.

Температура на границе слоёв i и i+1 можно найти следующим образом

.

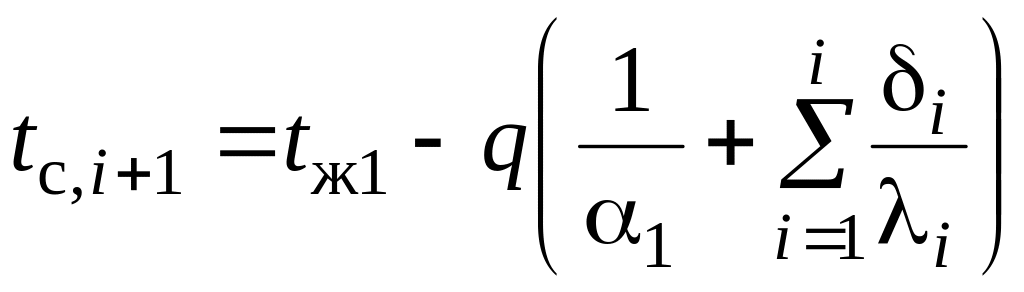4.2. Теплопроводность цилиндрической стенки

Рис.8. Расчётная схема

Перенос тепла в цилиндре описывается уравнением теплопроводности в цилиндрических координатах – r, , z (см. рис.8).

. (4.5)

Если коэффициент теплопроводности не зависит от температуры и при отсутствии источников внутреннего тепловыделения уравнение (4.5) можно упростить.

.

Если цилиндр находится в среде, температура которой по окружности цилиндра постоянна, то вдоль координаты переноса тепла не будет, поскольку в этом направлении . Если длина цилиндра стремится к бесконечности, то перенос тепла вдоль оси z также равен нулю. В таком цилиндре изотермические поверхности будут представлять соосные цилиндры (см. рис.8) и перенос тепла будет происходить только в направлении радиуса r. В стационарном тепловом режиме температура не зависит от времени и будет изменяться только по радиусу цилиндра. В результате уравнение примет вид

. (4.6)

Рассмотрим процесс переноса тепла в цилиндрической стенке (трубе) с внутренним диаметром и наружным диаметром (см. рис.9). Обозначим . Уравнение примет вид

. (4.7)

Интегрируя (4.7) получим

или

и . Заменяя u на dt/dr получим

.

После интегрирования найдём

.

Для определения постоянных С₁ и С₂ необходимо задать граничные условия.

а) граничные условия первого рода

Рис.9. Теплопроводность цилиндрической стенки

В этом случае при r=R1 и при r=R2 . ; . Отсюда ; . Таким образом, решение данной задачи имеет вид .

или

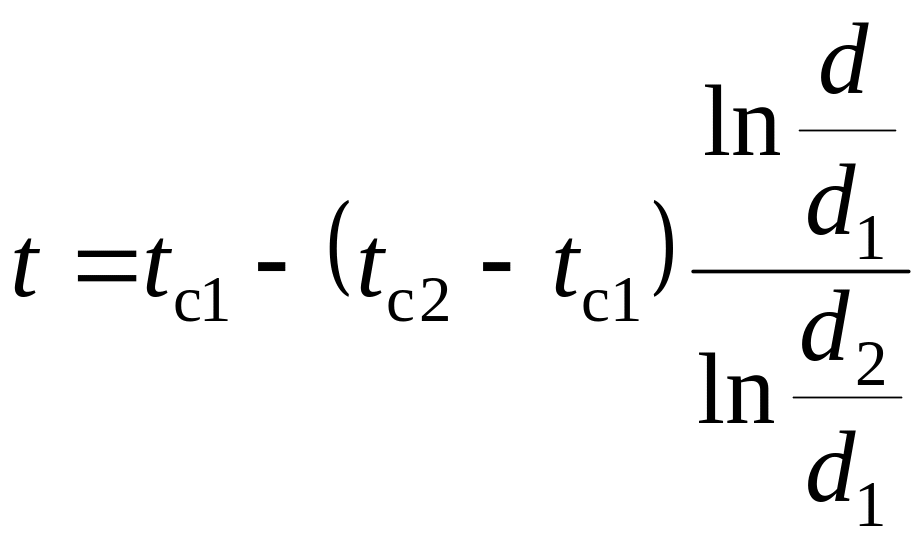. (4.8)

Как следует из (4.8), распределение температуры внутри цилиндрической стенки представляет собой логарифмическую кривую. Найдём плотность теплового потока.

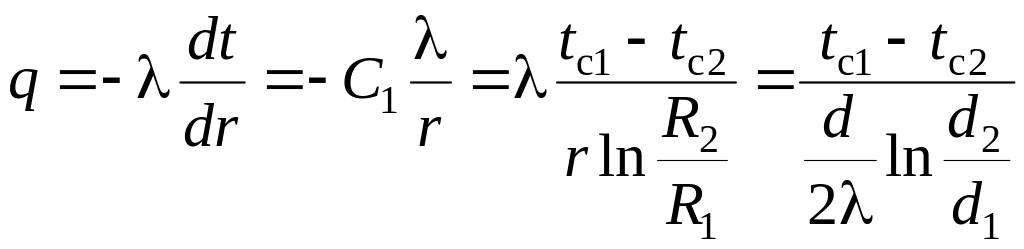, Вт/м².

Таким образом, для цилиндрической стенки плотность теплового потока через любую изотермическую поверхность зависит от радиуса (диаметра). Тепловой поток через цилиндрическую поверхность равен

, Вт.

Для единицы длины изотермической поверхности

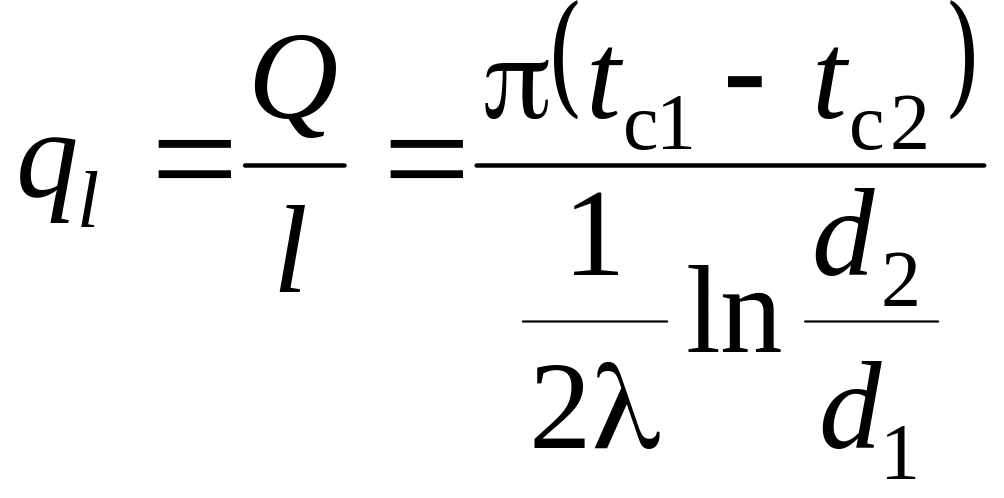, Вт/м.

Тепловой поток, отнесённый к единице длины поверхности, называется линейной плотностью теплового потока – . Таким образом, , где и плотности теплового потока на поверхностях диаметра и . Отсюда следует связь между линейной плотностью теплового потока и плотностями теплового потока.

; .

Величина , мК/Вт называется линейным термическим сопротивлением теплопроводности цилиндрической стенки. В случае многослойной цилиндри-

Рис.10. Многослойная цилиндрическая стенка

ческой стенки (рис.10) линейное термическое сопротивление равно сумме термических сопротивлений слоёв и линейная плотность теплового потока равна . Температура на границе любого слоя есть .

б) граничные условия третьего рода

Рис.11. цилиндрическая стенка

Будем считать, что цилиндр бесконечно длинный, поэтому можно пренебречь потерями тепла с торцов. Температуры жидкостей внутри и снаружи трубы, а также коэффициенты теплоотдачи постоянны. В таком случае тепло будет передаваться только по радиусу. В стационарном случае количество тепла, переданное от одной жидкости к стенке равно количеству тепла переносимо-

го теплопроводностью через стенку и равно количеству тепла, воспринятому другой жидкостью. Для единицы длины поверхности можно записать

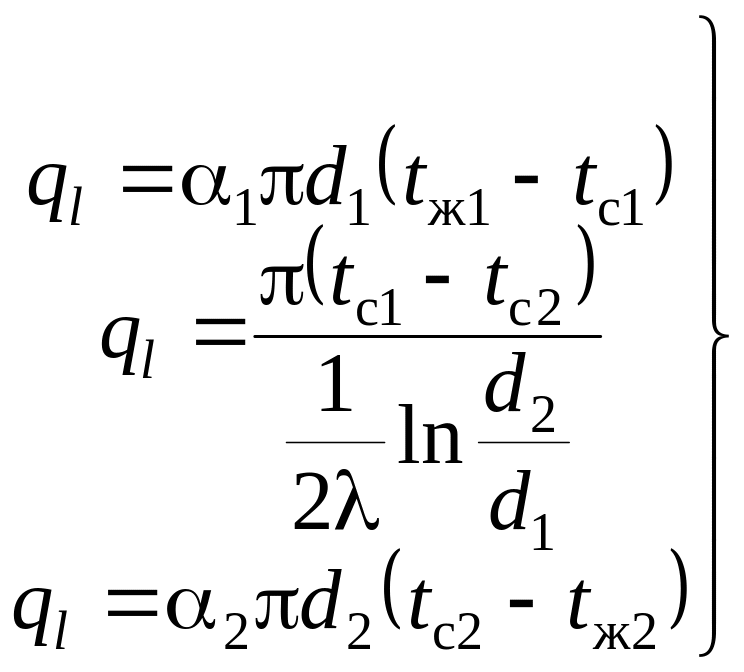(4.9)

Выразим из (4.9) разности температур и сложим получившиеся уравнения.

и определим

,

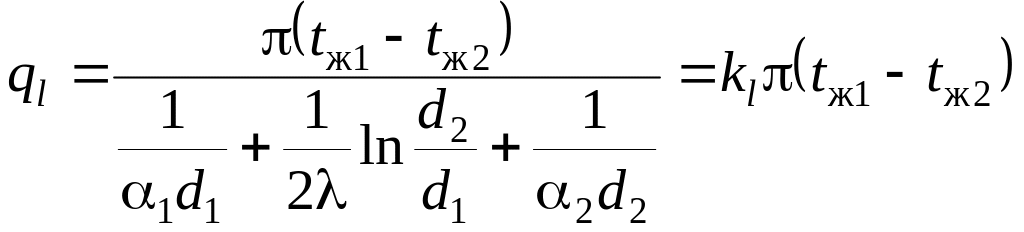где называется линейным коэффициентом теплопередачи

.

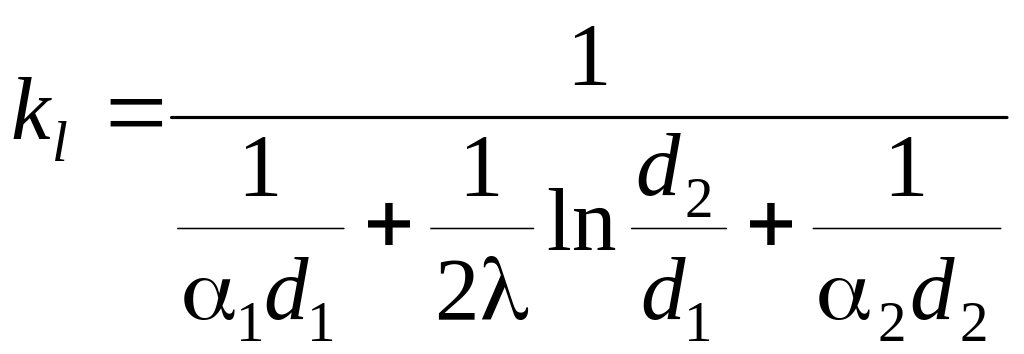Величина называется линейным термическим сопротивлением теплоотдачи. Для многослойной цилиндрической стенки

.
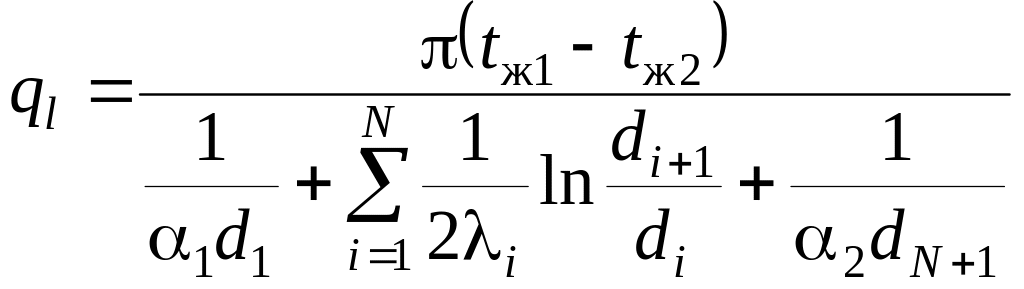
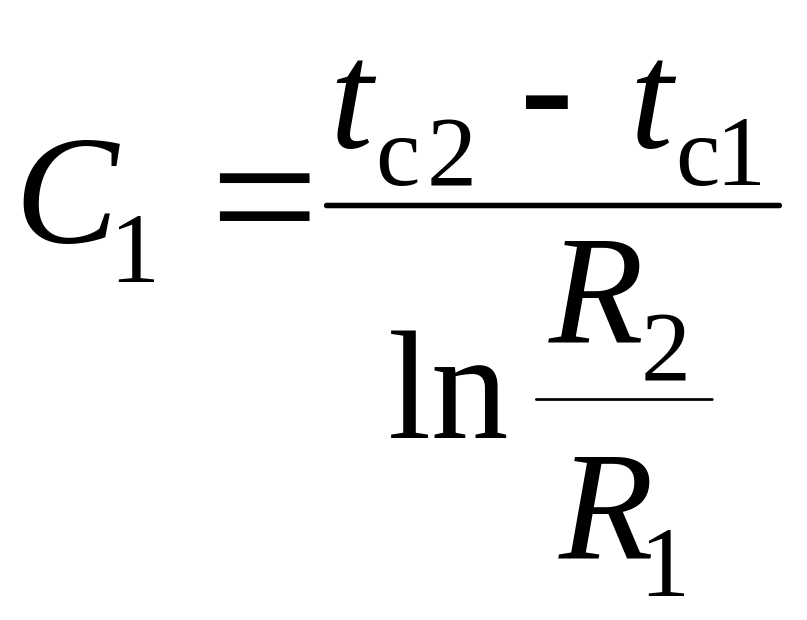
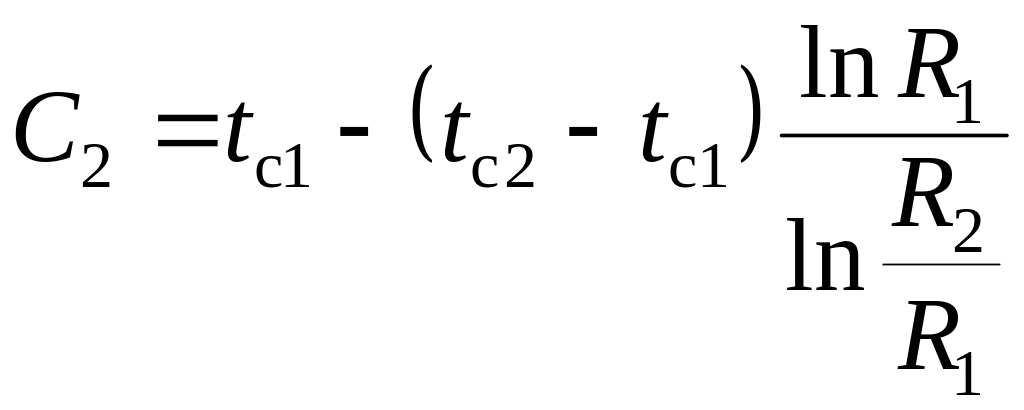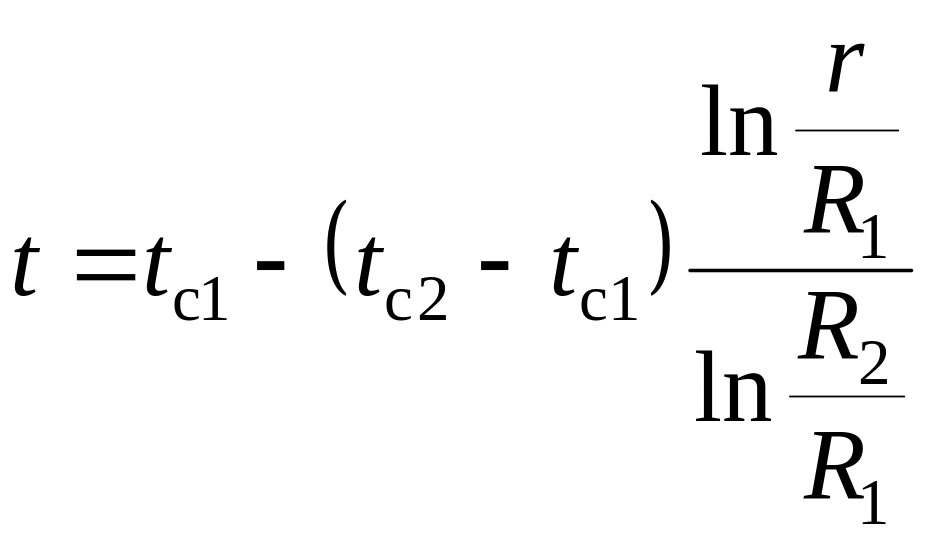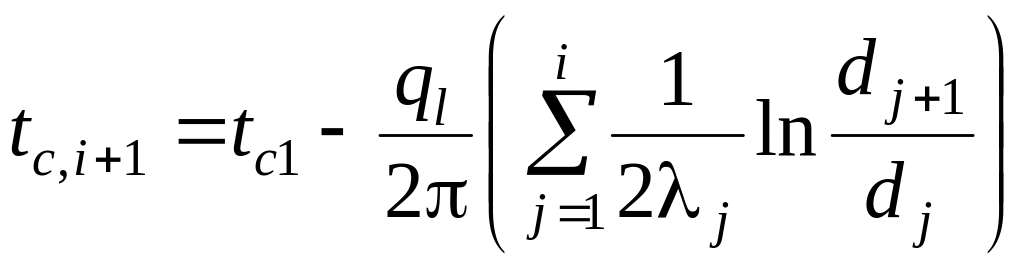