Добавил:

Tushkan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Уравнения математической физики. Методы математической физики.

Файл:

Лекции

.pdf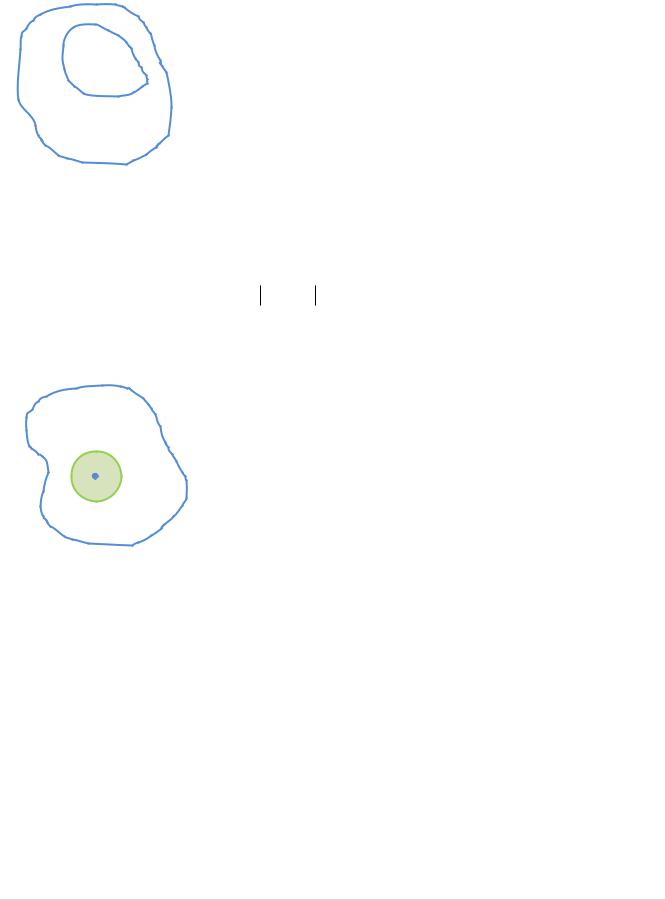

Скачиваний:

101

Добавлен:

28.06.2014

Размер:

1.25 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 66

Пусть U – гармоническая функция в области D . Тогда для любой замкнутой

подобласти D,

U d 0 .

Рассмотрим

произвольную

D .

Обозначим

через G – область, ограниченную и лежащую

внутри .

Функция

– гармоническая в

D .

Следовательно,

U C2 D . Так

как G

D , то

U C2

Используем

свойство

для

области

G :

n d 0

Теорема 1.

О среднем (для гармонических функций).

Пусть U – гармоническая функция в области D . Тогда для любой точки M0 D и любой сферы a M : M M0 a D

U M 0

4 a2

Из

интегрального

представления

для

гармонической

функции

(в

области

M :

M M0

a ):

M 0

U M 0

M M

n U

M M

1/ a

U d

M 0

M a

r a

U M 0

4 a

a n

4 a

0 (по следствию)

Захаров Антон, А-13-08 | http://a1308.ru

50 | С т р а н и ц а

Лекция № 13.

ПРИНЦИП МАКСИМУМА ДЛЯ ГАРМОНИЧЕСКИХ ФУНКЦИЙ.

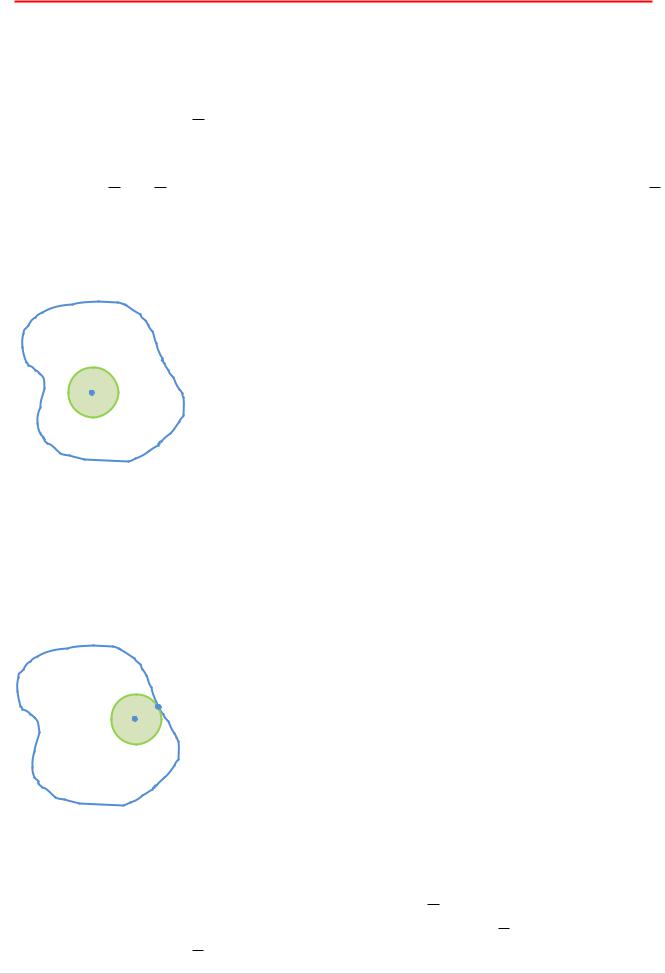
Пусть D – ограниченная область с границей .

Теорема 1.

Пусть функция U C D гармоническая в D , тогда функция U достигает своих в максимального и минимального значений на границе области.

Т. к. U C D и D – компакт, то функция U достигает максимального в D значения в некоторой точке. Предположим, что U достигает максимального

значения в

(то есть

внутри

области).

Следовательно,

M0 D : U M0 max U M .

M D

Окружаем M 0

сферой

с центром в точке M 0

радиуса ,так что D .

По теореме о среднем для гармонических функций

справедливо следующее равенство:

M 0

U M

U M d

U M

U M0

(1)

Поскольку

непрерывна

на

то

если

U M U M0

хотя бы в одной точке

M , то в

неравенстве (1) также будет знак «строго меньше»:

U M

M 0

U M0

Тогда U M0 U M0 – противоречие. Следовательно,

U M U M0 M ,

D .

Пусть 0 – расстояние от M 0

до . Рассматриваем

сферу с

центром

M 0

радиусом

0 .

Следовательно, M *

U C

U C M * .

Функция

и,

частности,

Следовательно,по определению непрерывности:

U M *

lim U

lim

U M

M M

M D

M 0

U M * U

max U M , M *

M D

Для минимума теорема доказывается аналогично.

Теорема 2.

Пусть D – связное множество, функция U C D гармонична в D . Если

функция U достигает максимального (минимального) в D значения внутри области, то U const в D .

Захаров Антон, А-13-08 | http://a1308.ru

51 | С т р а н и ц а

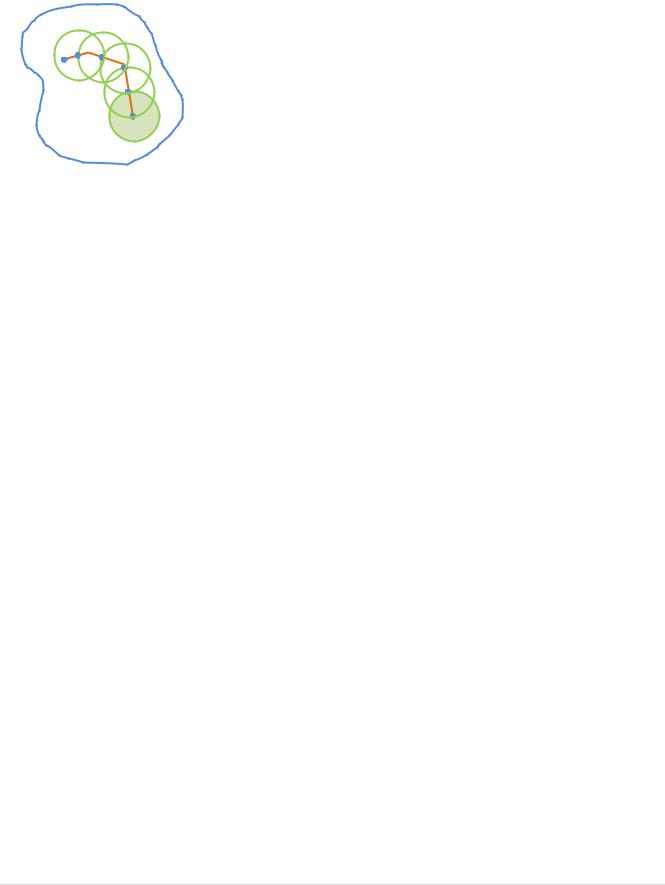
Предположим, что

U достигает максимального в

значения внутри

области,то есть M0 D : U M0 max U M .

M D

Докажем,что U M U M0 M

Рассмотрим

M D .

Соединяем

M 0

ломаной

l D .

Можем

это

M n

сделать,так как множество связное.

M 2

Пусть – минимальное расстояние от l

до . Пусть

M1 – последняя точка выхода

0 M :

D ,

ломаной

из

сферы

0 . По теореме о среднем

U M U M0 M 0

и M , лежащих внутри 0

(см.

доказательство теоремы 1).Следовательно, U M1 U M0 .

Далее рассматриваем сферу 1

– последняя

M :

D . Пусть M 2

точка выхода ломаной l

из сферы 1 . Аналогично получаем U M2 U M1 .

Кроме того, U M U M1 M внутри 1 .

И так далее...

За конечное число шагов получаем сферу n

M M n

M :

: M внутри n .

– произвольная точка D .

U M U Mn

U Mn 1 ... U M0 U M U M0

,где M

Рассмотрим M * .

U C

U C M * U M *

lim U M lim U M

M * U M

M *

M M

M D

Таким образом:

U M

0 M

U const

U M

M D

Захаров Антон, А-13-08 | http://a1308.ru

52 | С т р а н и ц а

СЛЕДСТВИЯ ИЗ ПРИНЦИПА МАКСИМУМА.

Рассмотрим задачу:

U 0 в D

(2)

Теорема 3.

Единственность решения задачи Дирихле.

Пусть U1, U2 C

– решения задачи (2). Тогда U1

Рассмотрим функцию V U1 U2 . Следовательно,

V U1 U2 0 в D ,

причём V C2 D .Следовательно, V – гармоническая в

Кроме того, U1,

U2 C

V C

. По принципу максимума V

достигает

своих максимального и минимального в

значений на границе области

D .

V M

M U1 U2 M

M U1 M

M U2 M

M M M 0 V

M 0

max V min V 0

min V V M

max V

0 V M 0 V M 0 M

U1 U2 M

Теорема 4.

U , V C

гармоничны в D .

Если U M V M M , то

Пусть функции

U M V M M

Рассмотрим W V U . Следовательно, W C

гармонична в D , тогда для

справедлив

принцип максимума, то есть функция W

принимает

минимальное в D значение на .

Если M W M V M U M 0 min W 0

W M min W 0 M D W M 0 M D U M V M M D .

Теорема 5.

Пусть функции U, V , W C D гармоничны в D .

Если U M V M W M M , то U M V M W M M D .

Следует из теоремы 4.

Теорема 6.

Пусть U C D гармонична в D .

Если U M , const 0 M , то U M M D .

Захаров Антон, А-13-08 | http://a1308.ru

53 | С т р а н и ц а

Рассматриваем три функции: , U , . Все функции непрерывны в D и гармоничны в D .Кроме того:

U M M U M M

По теореме 5 получаем:

U M M D U M M D

Пусть U – решение задачи:

U 0	в D
		(3)
		(3)
U

Пусть U * – решение задачи:

U * 0 в D
		(4)
U *	*
U *	*

Теорема 7.

Устойчивость решения задачи Дирихле.

Решение задачи Дирихле (3) в классе непрерывных в D функций устойчиво.

Фиксируем 0 .

Пусть

M * M

M .

Рассмотрим вспомогательную функцию V U U * . Следовательно, V M C

гармоническая в D .

V M

U U * M

U M

U * M

M * M

V M

Из теоремы 6 получаем:

V M

U M U * M

M D

Захаров Антон, А-13-08 | http://a1308.ru

54 | С т р а н и ц а

Экзаменационная программа.

А1308.

1.Классификация линейных уравнений 2-го порядка на плоскости. Уравнение характеристик.

2.Математическая модель малых колебаний струны.

3.Задача Коши для уравнения колебаний струны. Формула Даламбера.

4.Устойчивость решения задачи Коши для уравнения колебаний струны.

5.Постановка краевых задач для уравнения колебаний струны.

6.Краевая задача о малых колебаниях полуограниченной струны с закреплённым концом. Метод продолжения.

7.Решение первой краевой задачи для уравнения колебаний струны методом Фурье.

8.Интеграл энергии для волнового уравнения.

9.Единственность решения первой краевой задачи для уравнения струны.

10.Уравнение Лапласа. Постановка краевых задач для уравнения Лапласа.

11.Формулы Грина для оператора Лапласа.

12.Интегральное представление гармонических функций.

13.Свойства гармонических функций.

14.Теорема о среднем для гармонических функций.

15.Принцип максимума для гармонических функций.

16.Следствия из принципа максимума для гармонических функций. Устойчивость решения задачи Дирихле.

17.Единственность решения задачи Дирихле.

18.Задача Дирихле в круге. Метод Фурье.

19.Функция Грина задачи Дирихле. Решение задачи Дирихле с помощью функции Грина.

20.Вывод уравнения теплопроводности.

21.Постановка краевых задач для уравнения теплопроводности.

22.Принцип максимума для уравнения теплопроводности.

23.Следствия из принципа максимума для уравнения теплопроводности. Устойчивость решения первой краевой задачи.

24.Единственность решения первой краевой задачи для уравнения теплопроводности.

25.Решение первой краевой задачи для уравнения теплопроводности методом Фурье.

26.Задача Коши для уравнения теплопроводности. Интеграл Пуассона.

27.Единственность решения задачи Коши для уравнения теплопроводности.

Захаров Антон, А-13-08 | http://a1308.ru

55 | С т р а н и ц а

<<< < Предыдущая 1 2 3 4 56 / 66

Соседние файлы в предмете Уравнения математической физики. Методы математической физики.

#
28.06.2014270.69 Кб240Задачи Штурма-Лиувилля.pdf
#
28.06.20142.15 Mб75Кузнецов Л. Сборник заданий по высшей математике (типовые).djvu
#
28.06.20141.25 Mб101Лекции.pdf
#
28.06.20141.25 Mб71Лекции_2.pdf
#
28.06.2014652.43 Кб381Типовые.pdf
#
28.06.201427.65 Кб20Экзаменационная программа.doc