3 Расчет ступенчатой колонны

3.1 Расчётные усилия в колонне

По результатам статического расчёта для верхней части колонны из двух расчётных сечений (3-3 и 4-4) выбирается сочетание нагрузок с максимальными абсолютными значениями изгибающего момента и продольной силы. Для нижней части колонны из расчётных сечений (1-1 и 2-2) выбирается два сочетания нагрузок с максимальными абсолютными значениями изгибающего момента и продольной силы , при этом одно сочетание с отрицательным изгибающим моментом (момент догружает подкрановую часть колонны), второе сочетание с положительным изгибающим моментом (момент догружает наружную ветвь колонны).

Расчётные комбинации усилий в колонне:

1. Для верхней части колонны в сечении 4-4:

M = 1479,478 кН·м, N = -368,703 кН, Q = 203,981 кН (1,2,4,6,8);

в сечении 3-3 при том же сочетании нагрузок получим: М = 412,189 кН·м

2. Для нижней части колонны:

M = -2450,196 кН·м, N = -766,021 кН, Q = 267,676 кН (1,2,4,5,8);

M = 1858,225 кН·м, N = -486,64 кН, Q = 169,526 кН (1,2,3,6,7).

В дальнейших расчетах знаки усилий можно опустить.

3.2 Расчётные длины колонны

Расчетные длины для нижней и верхней частей колонны в плоскости рамы определяем по формулам:

(3.1)

(3.2)

где ;

Определим моменты инерции верхней и нижней части колонны по формулам:

(3.3)

(3.4)

где - опорная реакция ригеля рамы ( );

- сосредоточенная нагрузка на колонну от снеговой нагрузки

- максимальное давление от действия крана ( );

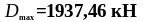- высота сечения нижней части колонны ( );

- расчётное сопротивление стали ( );

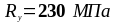- высота сечения верхней части колонны ( );

Поставив значения в формулы (3.3) и (3.4) получим:

Соотношение погонных жесткостей верхней и нижней частей колонны равно:

(3.5)

где

(3.6)

где - продольное усилие в нижней части колонны ( );

- продольное усилие в верхней части колонны ( ).

Подставив значения в (3.6) получим:

Подставив значения в (3.5) получим:

Для однопролетной рамы с жестким сопряжением ригеля с колонной (верхний конец колонны закреплен только от поворота) по СНиП II-23-81* (табл.68, стр.105) [8] , тогда:

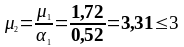
Так как условие не выполняется, то принимаем .

Таким образом, для нижней части колонны:

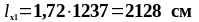
Для верхней части колонны:

Расчетные длины из плоскости рамы для нижней и верхней частей колонны равны соответственно:

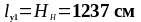
3.3 Подбор сечения верхней части колонны

Верхнюю часть колонны принимаем из сварного двутавра высотой h_в = 1000 мм. Из условия устойчивости определяем требуемую площадь сечения. Для симметричного двутавра:

Условная гибкость стержня:

(3.7)

где - расчётное сопротивление стали ( );

_{- модуль упругости} ( );

Подставив значения в формулу (3.7) получим:

Относительный эксцентриситет:

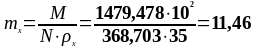
Принимаем приближено А_f /A_w = 0,5, тогда коэффициент влияния формы сечения (табл.73, стр.111) [8].

Приведённый относительный эксцентриситет:

По таблице 74 (стр.113) [8] при и коэффициент

Коэффициент условий работы для колонны .

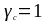Предварительно толщину полки принимаем .

Высота стенки:

Определим требуемую толщину стенки из условия ее местной устойчивости при изгибе колонны в плоскости действия момента:

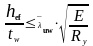(3.8)

Предельная уловная гибкость стенки при и 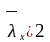(табл.27, стр. 45) [8].

Требуемая толщина стенки:

При этом из условия местной устойчивости стенки при изгибе из плоскости действия момента приближенно:

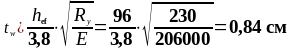
Принимаем толщину стенки t_w = 1 см.

Расчётная высота стенки, включающая два участка стенки, примыкающих к полкам:

(3.9)

где

Подставив значения в формулу (3.9) получим:

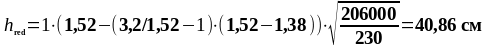
Требуемая площадь полки:

Ширина полки равна:

Из условия устойчивости верхней части колонны из плоскости действия момента:

Из условия местной устойчивости полки:

(3.10)

где

(3.11)

Подставив (3.11) в (3.10) и выразив b_f , получим:

(3.12)

Подставив значения в (3.12) получим:

По ГОСТ 82-70 [9] принимаем b_f = 560 мм.

Рисунок 3.1 - Сечение верхней части колонны

Вычисляем геометрические характеристики сечения.

Полная площадь сечения:

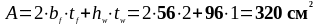
Расчетная площадь сечения с учетом только устойчивой части стенки:

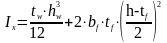(3.13)

Подставив значения в (3.13) получим:

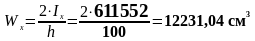
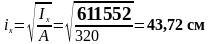
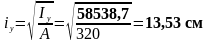
Проверяем устойчивость верхней части колонны в плоскости действия момента.

Гибкость колонны:

Т.к. 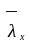незначительно отличается от предварительно принятой, то расчётную высоту стенки не уточняем.

Относительный эксцентриситет:

Так как , то коэффициент (табл.73, стр.111) [8].

Приведённый относительный эксцентриситет:

По таблице 74 (стр.113) [8] при 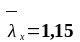и коэффициент

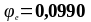
Гибкость колонны в плоскости рамы:

Проверяем устойчивость верхней части колонны из плоскости действия момента.

Гибкость колонны:

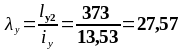
По таблице 72 (стр.110) [8] коэффициент .

Максимальный момент в средней трети расчётной длины стержня:

Относительный эксцентриситет:

Так как , то коэффициент с определяем по формуле (58) (стр.22) [8]:

(3.14)

где

Подставив значения в формулу (3.14), получим:

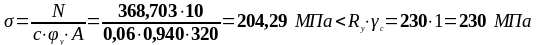
Гибкость колонны из плоскости рамы:

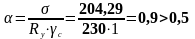
Проверяем местную устойчивость полки колонны. Свес полки:

Так как:

то местная устойчивость полки обеспечена.

Проверяем местную устойчивость стенки при изгибе колонны из плоскости действия момента. Наибольшее сжимающее напряжение на краю стенки:

Напряжения на противоположном краю стенки:

Средние касательные напряжения в стенке:

При наибольшее отношение определяем по формуле:

(3.14)

где

Подставим значения в формулу (3.14) и получим:

Принимаем .

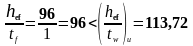
Местная устойчивость стенки обеспечена.