Лабораторные работы / Ганишев (8 вариант) / Лабораторная работа 1

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Лабораторная работа №1

«Предельные теоремы»

по дисциплине «Теория вероятности

и математическая статистика».

Выполнил: .

Студент группы А-13-08

Ганишев Василий

Проверил: .

Тигетов Д.Г.

Задание 1.

Вероятность появления герба p=0.5. Можно показать (с помощью центральной предельной теоремы), что, например, если n >=(1.5/eps)^2 , то соотношение |m/n-p|<eps выполняется с вероятностью 0.997, а если n>=(1.3/eps)^2, то - с вероятностью 0.99; последняя в данном случае нас устраивает как практическая достоверность. Положим eps = 0.1, тогда соотношение:

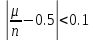(а)

Выполняется с вероятностью 0.99 при . Если 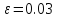, то соотношение

(б)

Выполняется с вероятностью 0.99, при . Мы уверены, что проведя 170 бросаний монеты получим (а), проведя 1850 получим (б).

Бросание монеты моделируем генерацией случайной величины 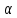, принимающей значения 1(«герб») и 0(«цифра») с вероятностями 0.5. Число появлений «герба» в n испытаниях

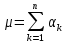, где – результат k-го испытания.

Решение.

Сгенерируем вектор длины 1850, компоненты которого принимают значения 0 или 1, с вероятностью 0.5

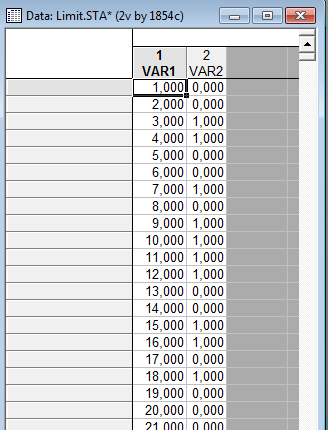
Выделим первые 170 значений и определим количество появления герба в 170 испытаниях, а также его относительную частоту

Убедимся, что

Проведём то же самое для 1850 испытаний

Отсюда видно, что

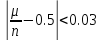
Задание 2.1

Проверить выполнение соотношения 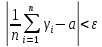экспериментально для экспотенциального распределения слагаемых с 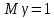. Принять и .

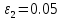Решение.

Подставив в неравенство 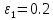и , получаем соответственно n = 135 и n = 2160

Сгенерируем вектор размера 2160, компоненты которого имеют значения согласно экспотенциальному закону распределения

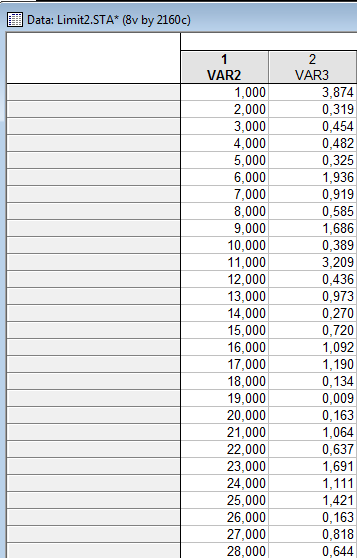
Выделим первые 135 строк и посчитаем значения среднеарифметического

Выделим все строки и проделаем то же самое

Как видно из этого соотношение выполняется.

Задание 2.2

Рассмотрим случайную величину, распределённую по закону Коши с плотностью

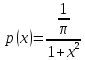
Заметим, что плотность симметрична относительно нуля, однако, 0 не является математическим ожиданием; это распределение не имеет математического ожидания. Напомним, что математическим ожиданием называется 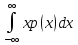, есть 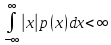; последнее, очевидно, для распределения Коши не выполняется. Для последовательности независимых случайных величин, распределённых по закону Коши (3), закон больших чисел не выполняется. Если бы среднеарифметическое 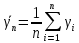сходилось с ростом n к какой-либо константе. То в силу симметрии распределения, такой константой мог быть только 0. Однако, 0 не является точкой сходимости. Действительно, можно показать, что при любом 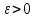при любом сколь угодно большом n 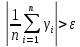с вероятностью

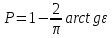
Сгенерируем 7 выборок по закону распределения Коши

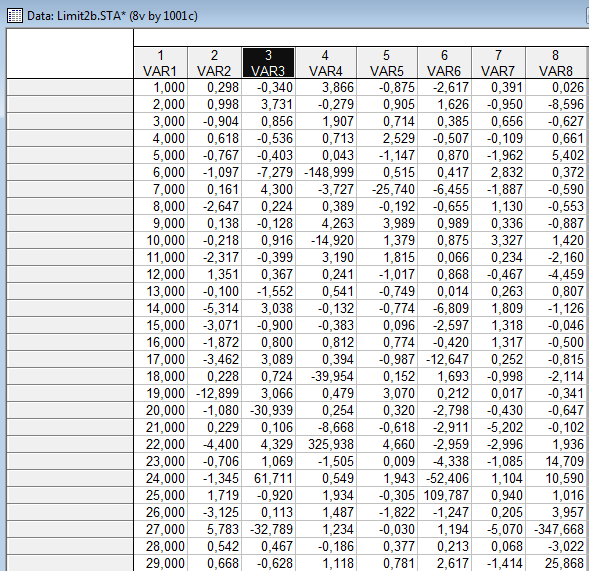
В трёх выборках модуль среднего превосходит 1

Приведём график выборки из распределения Коши

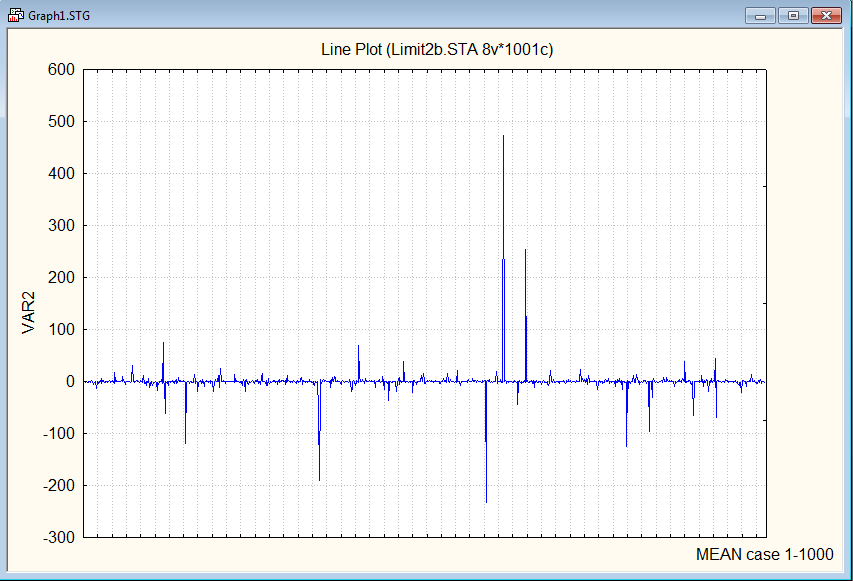
Задание 2.3

Закон больших чисел в форме Чебышева означает, что распределение случайной величины сжимается с ростом n. Если математические ожидания одинаковы, то сжатие происходит в окрестности этой точки.

Убедиться в сжатии можно, наблюдая гистограммы при различных значениях n(например, для n = 10, 40, 160, 640). Сгенерируем k раз случайную величину и построим для этой выборки средних гистограмму. Сравнивая гистограммы для различных n, мы заметим сжатие.

Графики плотностей нармального закона при различных

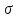
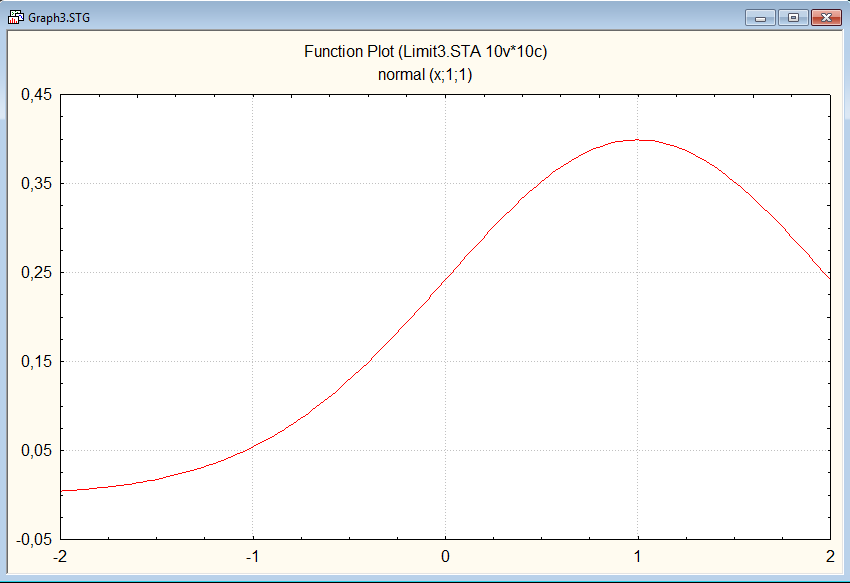
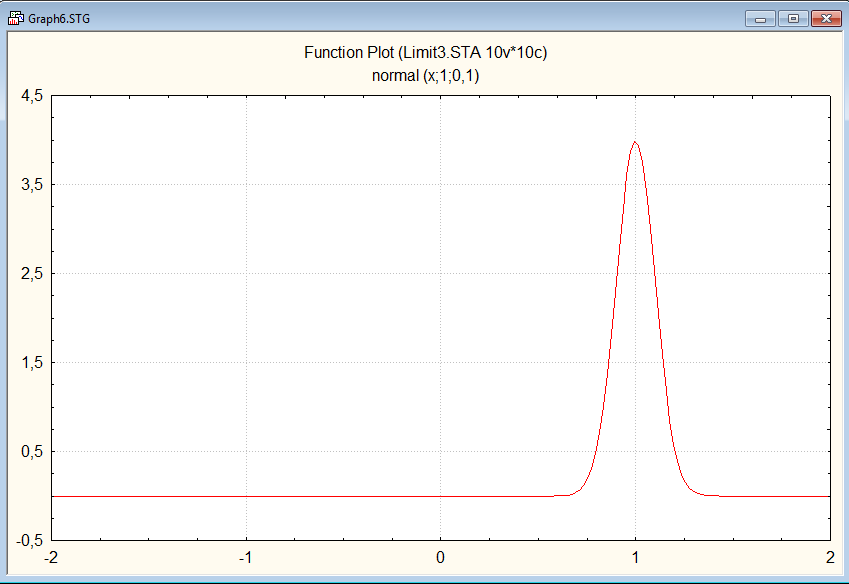
Сгенерируем 20 выборок объемом 640 из равномерного распределения на [0,1]. По всем выборкам для n = 10 определим среднее, стандартное отклонение, минимум и макимум. Повторяем действия для n = 40, 160, 640. Заметим, что при возрастании n разброс средних уменьшается. Транспонируем строки средних и построим график

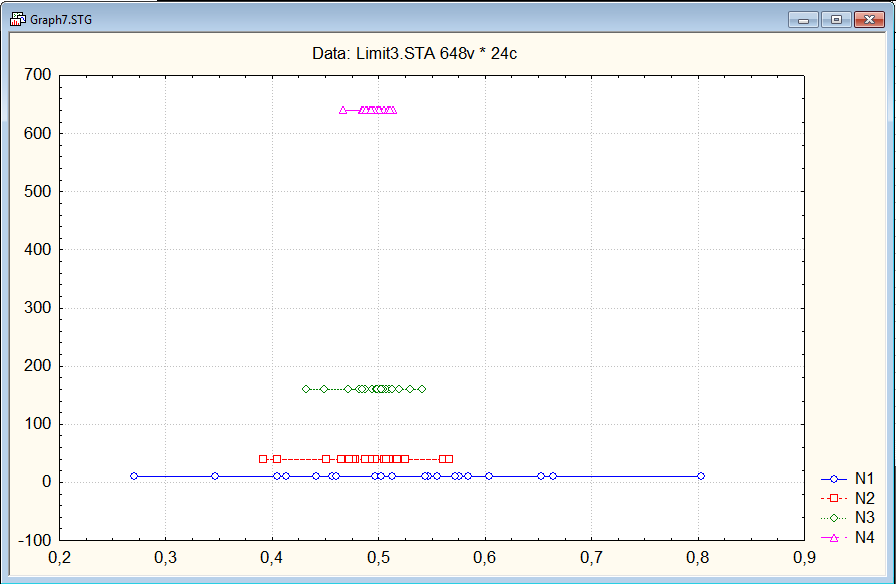
Задание 3

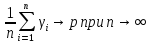Проиллюстрируем то, что на примере бросания симметричной монеты, а на примере равномерно распределённых на [0,1] случайных велечин.

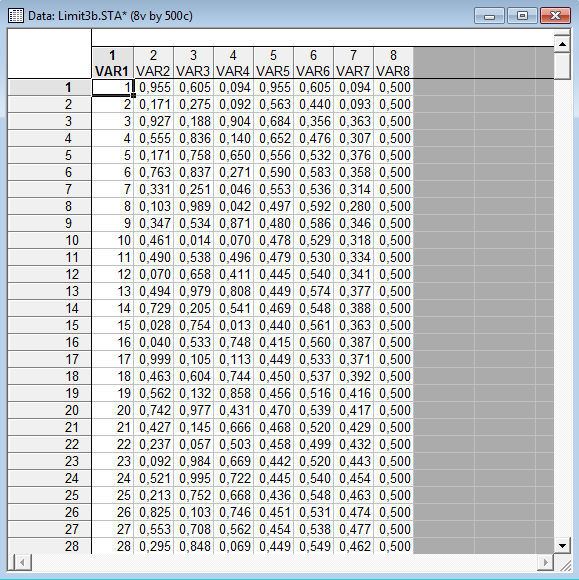
А) Сгенерируем 3 последовательности по 500 бросаний монеты в первых 3 столбца таблицы. Образуем последовательность среднеарифметических, исходя из соотношений:

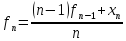, для n = 2,…,N

Для этого составим программу

Посмотрим графически зависимость f_n от n в различных диапазонах и отметим, что с возрастанием n частота выпадания герба приближается к p = 0.5.

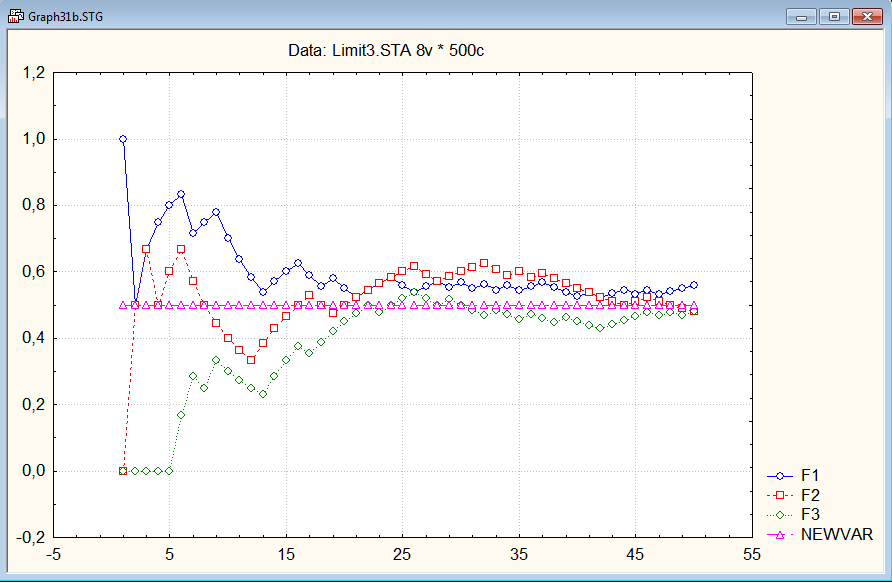
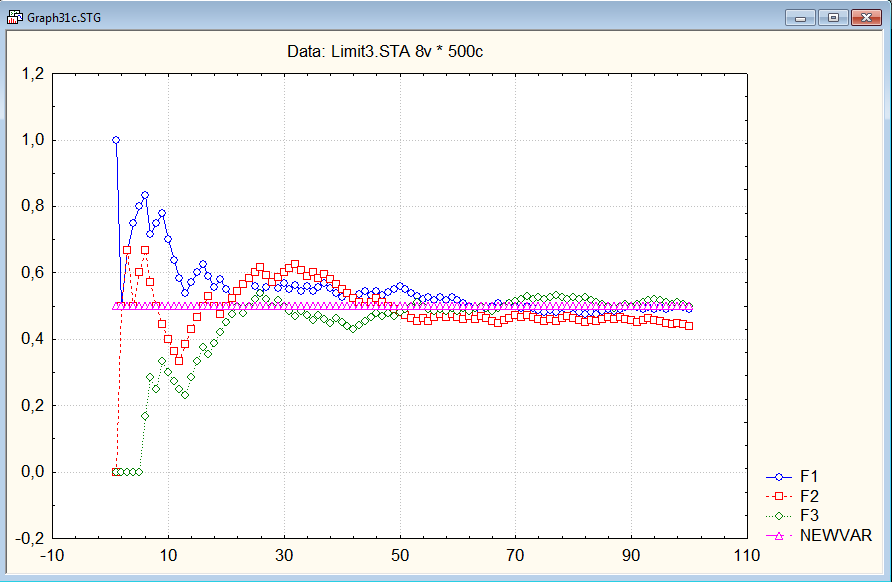
Б) Действия аналогичны пункту А.

В) Пример невыполнения закона.

Посмотрим на последовательностях случайных чисел, распределённых по закону Коши.

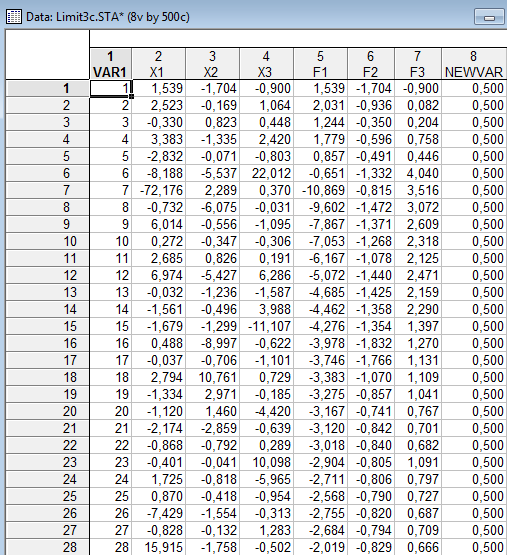
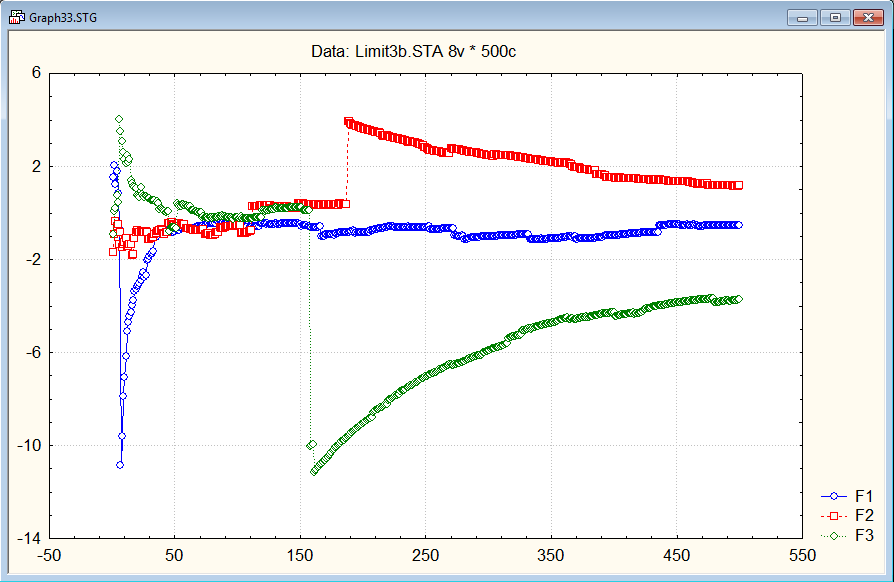
Видим, что кривые иногда испытывают скачки, отбрасывающие их значения далеко от 0 – центра распределения.

Задание 4

Проиллюстрируем теорему Гливенко на примерах наблюдения над случайной величиной, распределённой по равномерному закону на отрезке [0,1].

Сравним функцию эмпирического распределения для выборок объёмами 10, 40, 160, 640 с функцией теоретического распределения.

Сделаем таблицу в первый столбец запишем случайную величину, во второй – эмпирическую функцию распределения. А в третий – теоретическую. А затем выведем графики для каждого n.

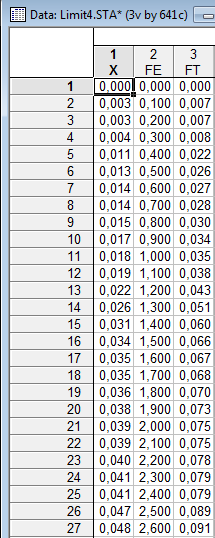
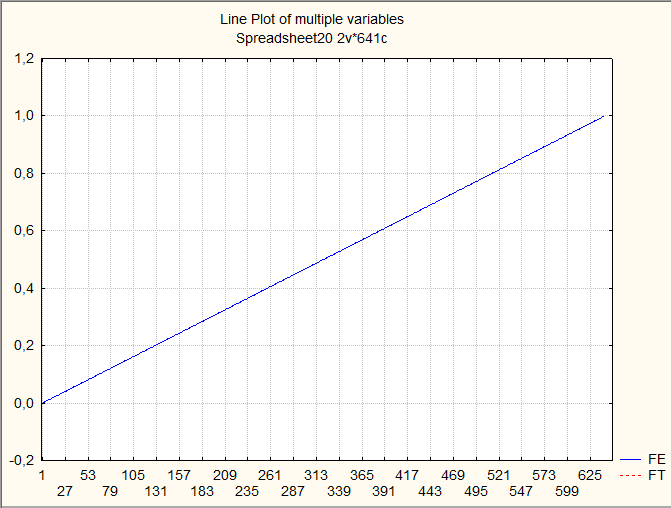
Задание 5

1. Одинаково распределённые слагаемые.

Сделаем это на примере суммы 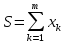шести независимых случайных величин, имеющих beta-распределение с параметрами a=b=0.5. плотность которого

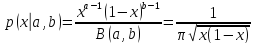
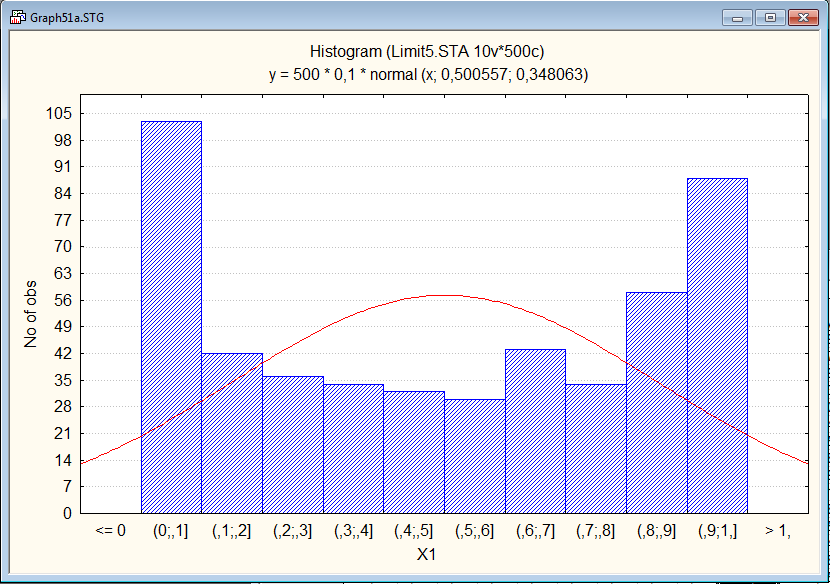
, где B(a,b) = – beta-функция. Плотность при выбранных значениях параметров имеет U-образный вид. Весьма далёкий от нормального; убедимся в этом. Построив график плотности.

2. Оценить экспериментально распределение для суммы шести слагаемых, распределённых по различным законам из семейства beta-распределений:

	1	2	3	4	5	6
a	1	0.5	1	1	2	2
b	0.5	1	1	2	1	2

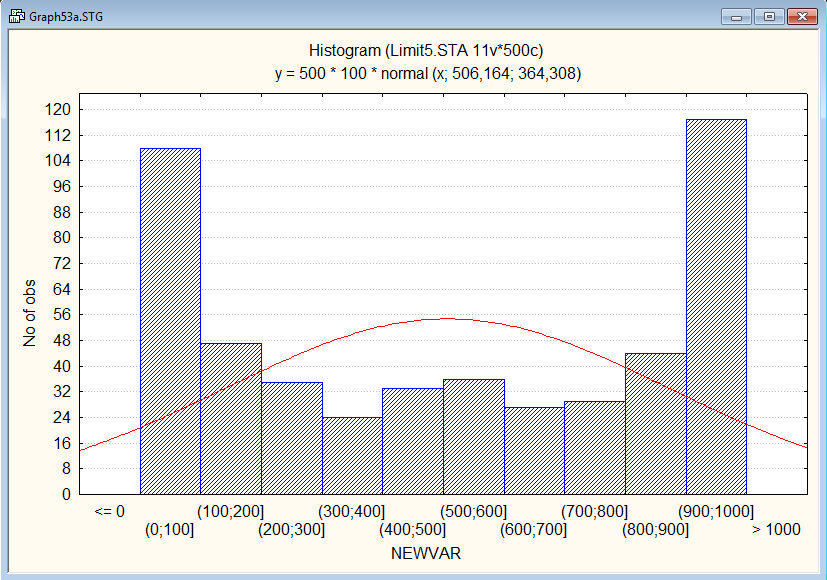
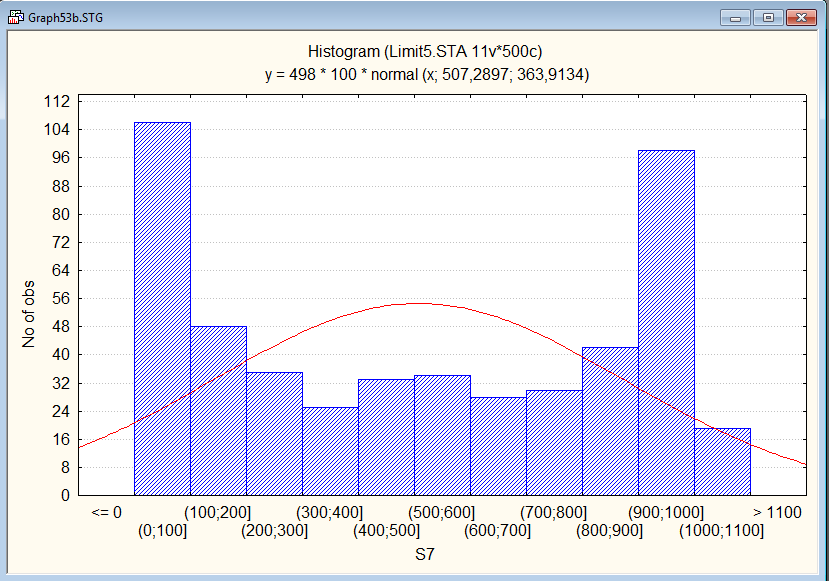
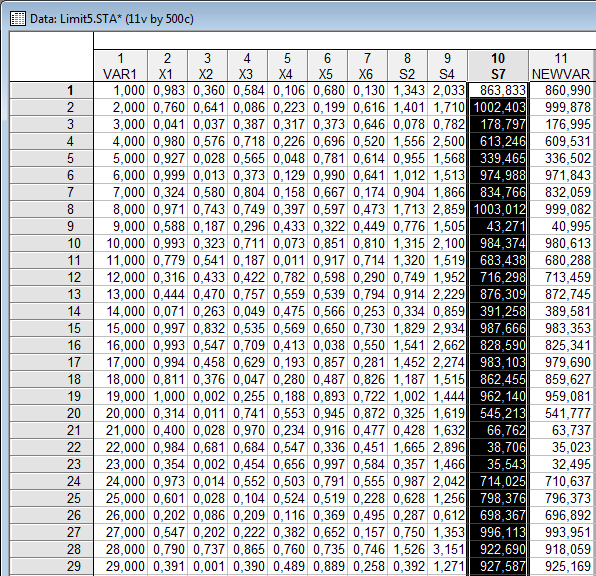
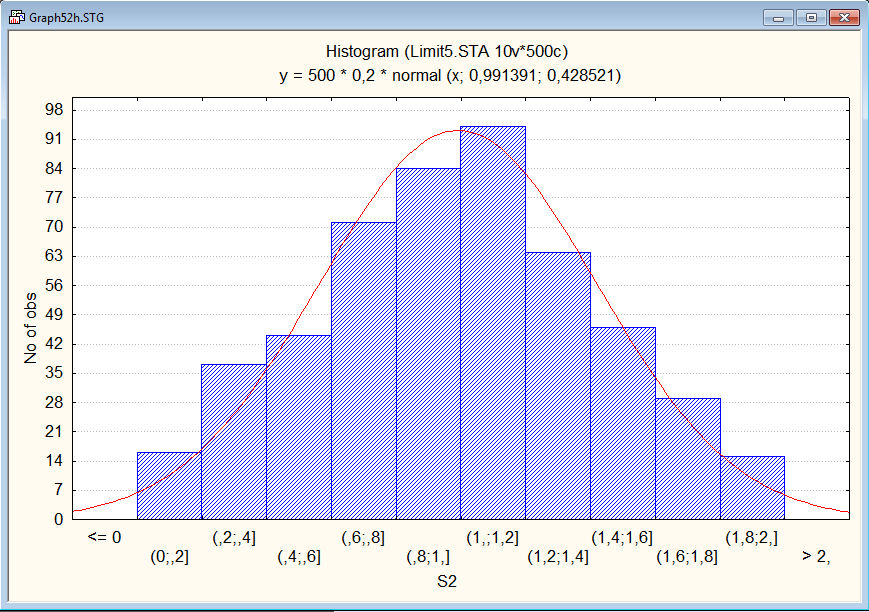
Сгенерируем выборку для суммы и построим гистограмму для неё. Убедимся в том, что распределение близко к нормальному

3. Если одно из распределений имеет дисперсию, которая существенно превышает все остальные, то приближенная нормальность места не имеет.

Добавим в таблицу ещё один столбец, где будет beta-распределение с параметрами a=b=0.5, умноженное на 1000