Лабораторные работы / Ганишев (8 вариант) / Лабораторная работа 6

МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Лабораторная работа №6

«Различение двух простых гипотез гипотез»

по дисциплине «Теория вероятности

и математическая статистика».

Выполнил: .

Студент группы А-13-08

Ганишев Василий

Проверил: .

Тигетов Д.Г.

Задание 1.

На вход канала связи подается сигнал S, который может принимать 2 значения:

S = 0(сигнала нет) и S = a != 0(сигнал есть)

В канале действует аддитивная ошибка ε, нормально распределенная со средним значением Mε = 0 и дисперсией Dε = σ²; результатом является x’ = S + ε. Измерения повторяются n раз. Так что на выходе имеются наблюдения (x₁,…,x_n) = x, по которым нужно решить, есть ли сигнал (Н₁: S = a) или нет (Н₀: S = 0). Требуется построить решающее правило δ, имеющее вероятность α₀ ошибки первого рода (вероятность ложной тревоги). α = P(принять H₁|H₀) = α₀ при минимальном значении вероятности β ошибки второго рода (вероятности пропуска). Считая ошибки независимыми, с учетом того, есть ли сигнал (H₁) или его нет (H₀) имеем:

р₁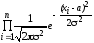(х) = , р₀(х) = .

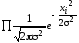В соответствии с (3), решение о наличии сигнала нужно принять (принять Н₁), если х попадает в Г₁, где

Г₁===.

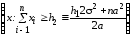Итак, если

,

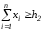то принимается Н₁; в противном случае принимается Н₀. Порог h₂ определяется из (4):

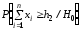(h₂) = P{пр. Н₁ / Н₀} = = ₀.

если верна Н₀, то 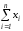распределена нормально со средним 0 и дисперсией n², и потому последнее условие принимает вид:

(h₂)= 1 - Ф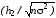= ₀ ,откуда

h₂ = Q(1 - ₀),

где Ф(х) - функция нормального N(0, 1) распределения; Q(1 - ₀) - квантиль порядка (1 - ₀) этого распределения.

Определим вероятность  ошибки второго рода для процедуры (5) с порогом (6). Если верна Н₁, то распределена нормально со средним na и дисперсией n², и потому

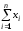
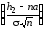 = P(пр.Н₀ /H₁)= P { h₂ /H₁} = Ф = Ф(Q - ).

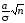Положим, а = 0.2,  = 1.0 (т.е. ошибка  в 5 раз больше сигнала а), n = 500,  = 10^-2 ; при этом

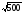
h₂ = 1   2.33 = 52,  = Ф(2.33 - 0.2  22.4) = Ф(-2.14) = 1.6  10^-2;

как видим, вероятности ошибок невелики: порядка 10^-2.

Проиллюстрируем этот пример статистически. Сгенерируем две выборки объема n = 500 в соответствии с гипотезами Н₀ и Н₁. Для обеих выборок построим гистограммы (в диапазоне от -2.5 до 2.5) и убедимся, что “на глаз” различие не заметно. Определим сумму наблюдений по каждой выборке и применим решающее правило (5) с порогом (6). Убедимся, что в обоих случаях решающее правило дает правильное решение.

Отсутствие сигнала:

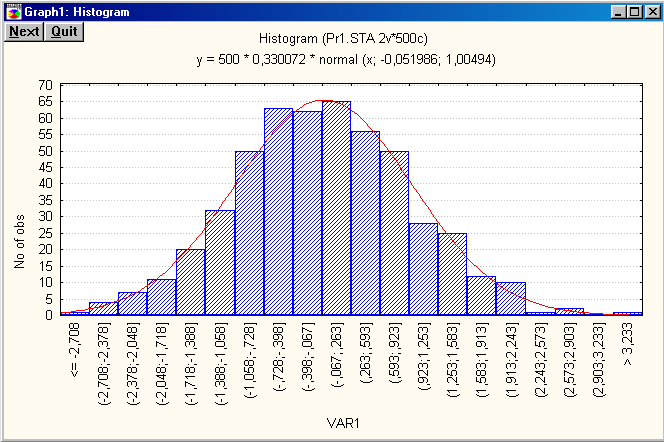
Наличие сигнала:

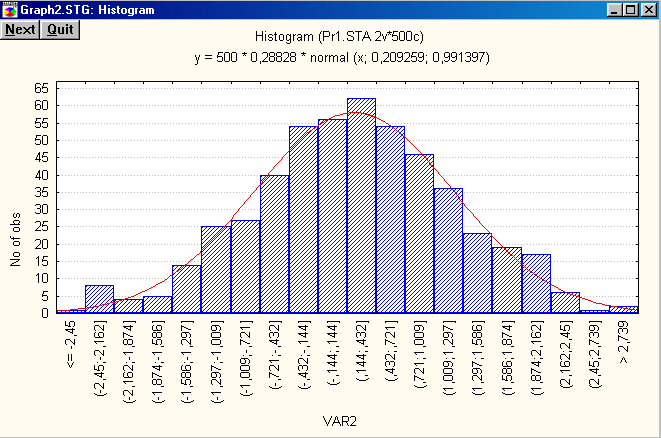
Суммы по выборкам:

В первом случае сумма меньше порога, отсюда следует, что принимается гипотеза об отсутствии сигнала. Во втором случае сумма больше порога, принимается гипотеза о наличии сигнала.

В обоих случаях решающее правило дало правильное решение.

Задача.

Радиоактивные вещества A и B излучают пуассоновские потоки частиц интенсивности λ_A сек^-1 и λ_B сек^-1, λ_A != λ_B. В закрытой капсуле находится одно из этих веществ, но неизвестно, какое именно.

1. Определить необходимое время T наблюдения излучения и статистическую процедуру(Неймана – Пирсона) определения вещества в капсуле. Процедура должна иметь заданные вероятности  и  ошибок первого и второго рода. Смоделировать измерения для двух случаев вещества(A и B), применить к ним процедуру и выяснить, верные ли решения принимаются.

2. Построить последовательную процедуру определения вещества. Определить среднее время наблюдения и функцию мощности, как функцию параметра. Смоделировать процесс наблюдения и принятия решения в двух случаях(по одной реализации). Изобразить его графически.

λ_A = 0.16

λ_B = 0.20

 = 0.03

 = 0.05

Решение.

Построим процедуру различения гипотез при фиксированном объеме выборки:

p_A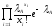(x) = , р_B(x) = .

Г_A===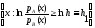

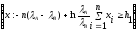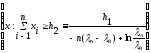
(h₂) = P{пр. Н_A / Н_B} = 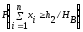= ₀

По закону больших чисел:

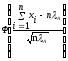, зн. (h₂) = 1 - = , h₂ =

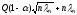
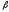= P{пр. Н_B / Н_A } =

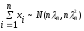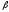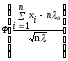, зн. = , h₂ =

=

=

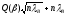
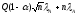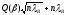
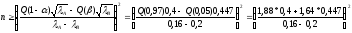=1378

h₂= 248,395

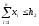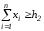В первом случае , следовательно, принимается гипотеза о нахождении в капсуле первого вещества. Во втором случае , следовательно, принимается гипотеза о нахождении в капсуле второго вещества.

Убеждаемся в том, что по построенному правилу принимаются правильные решения.

Построим последовательную процедуру различения гипотез.

Код процедуры последовательного анализа Вальда дан в приложении.

Графики(случай,когда находится первое вещество) даны в приложении

Процедура, моделирующая последовательный критерий даёт ответ на выборке объема 44 , а статической процедуре для этого требуется 248.

Приложение.

RandomAccess;

lambdaa := 0.16;

lambdab := 0.2;

_alpha := 0.03;

_beta := 0.05;

n := 0;

sums := 0;

k:=10;

Function SampleValue(BYREF cumulative, BYVAL length) (построение выборки по закону распределения А, аналогично в другой процедуре по Б)

begin

dim cumulative(length);

probability := Rnd(1);

SampleValue := length;

for i := 1 to length do

begin

if probability < cumulative(i) then

begin

SampleValue := i - 1;

i := length + 1;

end;

end;

end;

epsilon := 0.0001;

Dim cumulative_probability(1);

poisson_probability := exp(-lambdab);

cumulative_probability(1) := poisson_probability;

for i := 1 to 1000 do

begin

ReDim cumulative_probability(i+1);

poisson_probability := poisson_probability*lambdab/i;

cumulative_probability(i+1) := cumulative_probability(i) + poisson_probability;

if 1 - cumulative_probability(i+1) < epsilon then

begin

cumulative_length := i+1;

i := 1000 + 1;

end;

end;

for i:=1 to k do

begin

x := SampleValue(cumulative_probability, cumulative_length);

n := n+1;

data(n,1) := x;

sums := sums + x;

end;

loop:

x := SampleValue(cumulative_probability, cumulative_length);

n := n+1;

data(n,1) := x;

sums := sums + x;

data(n,6) := sums;

right := log(_beta/(1-_alpha)) - n*(lambdab - lambdaa);

right:= right / log(lambdaa/lambdab);

data(n,4) := right;

left := log((1-_beta)/_alpha) - n*(lambdab - lambdaa);

left := (-1) *right / log(lambdaa/lambdab);

data(n,5) := left;

if (sums <= left) then

begin

data(1,2) := 0.16;

goto done;

end;

if (sums >= right) then

begin

data(1,2) := 0.2;

goto done;

end;

goto loop;

done:

data(2,2) := n;

data(1,3) := left;

data(2,3) := right;

data(4,3) := sums;

M := 0.04 + log(0.8)*lambdaa;

data(6,3) := M;

data(7,3) := ( log(_beta/(1-_alpha))*(1- _alpha) + log((1-_beta)/_alpha) *_alpha) / M;

M := 0.04 + log(0.8)*lambdab;

data(8,3) := M;

data(9,3) :=( log(_beta/(1-_alpha))*_beta + log((1-_beta)/_alpha) *(1- _beta)) / M;