3. Усиленный закон больших чисел.

Теорема Бореля.

Относительная частота 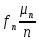появления случайного события с ростом числа 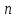независимых испытаний стремится к истинной вероятности .

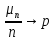Последовательность случайных величин 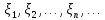подчиняется усиленному закону больших чисел, если

при n 

с вероятностью 1.

Теорема Колмогорова.

Если последовательность взаимно независимых случайных величин 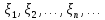удовлетворяет условию , то она подчиняется усиленному закону больших чисел.

Для независимых и одинаково распределённых случайных величин справедлива:

Теорема.

Необходимым и достаточным условием для применимости усиленного закона больших чисел к последовательности независимых величин является существование математического ожидания.

Воспользуемся теоремой Бореля в эксперименте с бросанием симметричной монеты.

Из последовательности x₁ ,..., x_N независимых наблюдений построим последовательность f₁, ..., f_N среднеарифметических, где

f_n = , n = 1, ..., N

и убедимся графически в том, что f_n c ростом приближается к математическому ожиданию.

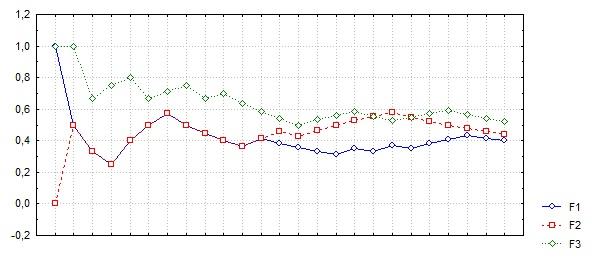
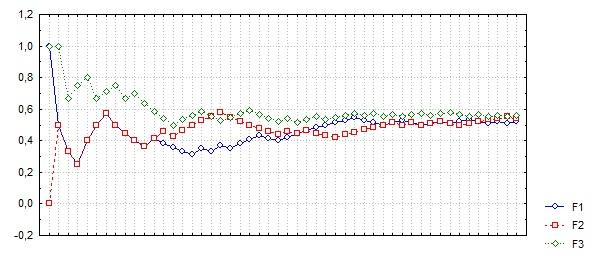
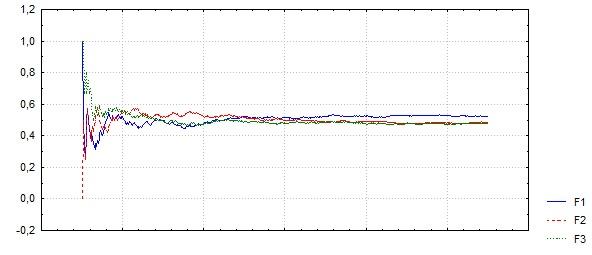
В этом эксперименте получено практическое подтверждение справедливости теоремы Бореля.

Для величин, распределённых по равномерному закону R[0,1]:

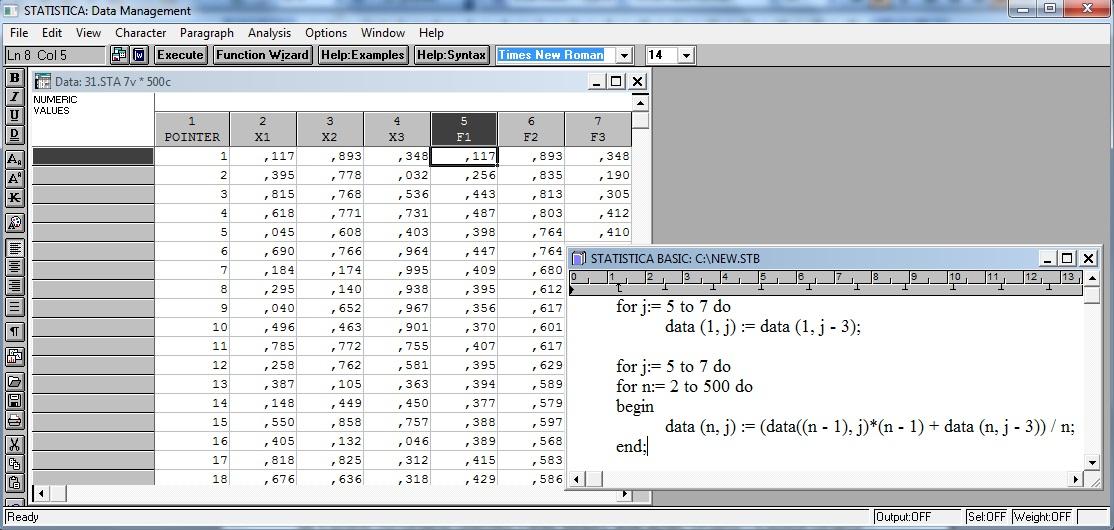
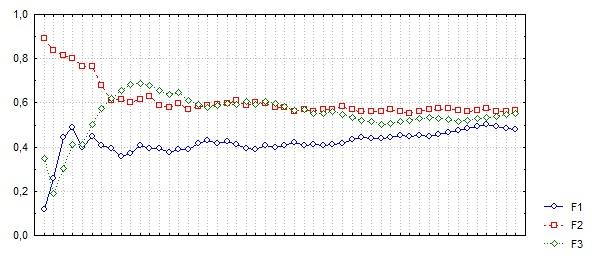
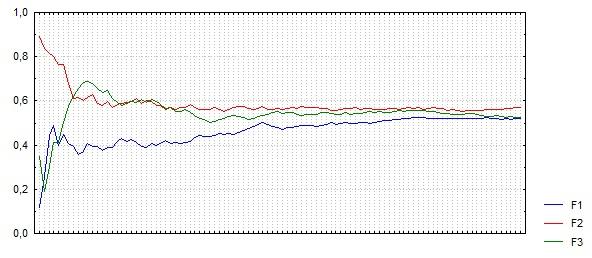
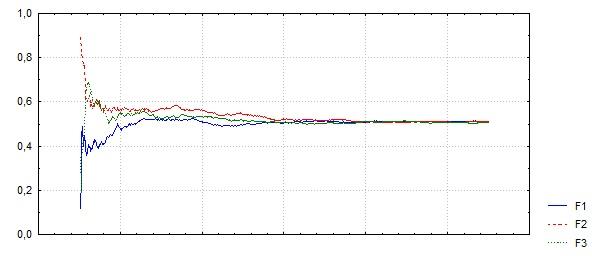
Средние арифметические случайных величин устремляются к своим математическим ожиданиям с ростом их числа.

Рассмотрим ситуацию, когда рассматриваемая случайная величина подчиняется закону распределения Коши. В таком распределении у случайной величины математического ожидания не существует.

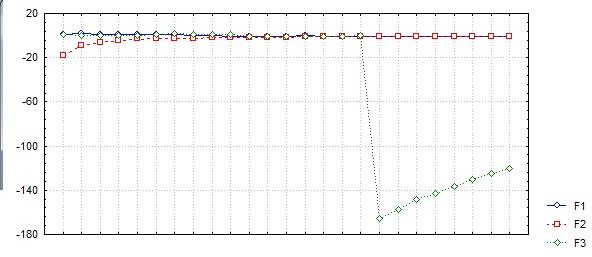
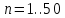
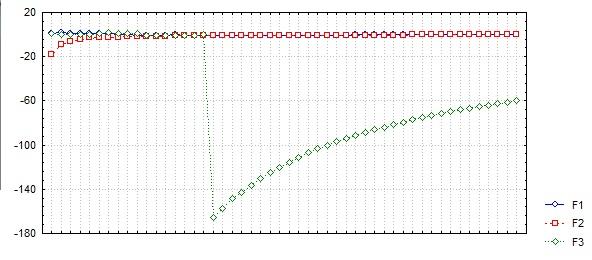
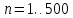
Экспериментально подтверждено, что случайные величины, распределённые по закону Коши, не удовлетворяют закону больших чисел.

Задание.

Промоделировать и посмотреть на графиках поведение среднего арифметического как функцию 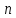для случайных величин, распределенных с плотностью

p(x) = ,

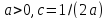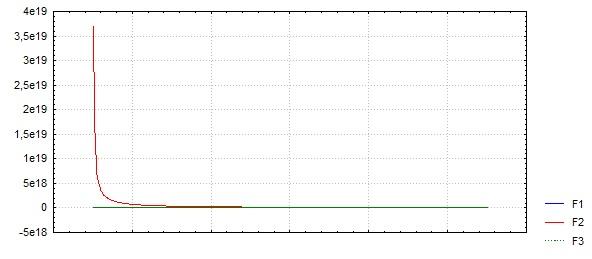
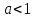где . При математическое ожидание существует, но при 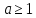это не так. При увеличении 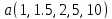скачки в среднем арифметическом (как функции 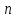) будут увеличиваться. Генерацию случайных чисел можно сделать по формуле

, где u ~ R[0,1],

a 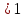с вероятностями .

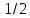Сгенерируем величины, с помощью функции (rnd(1)^(-1) -1)*sign(rnd(2)-1).

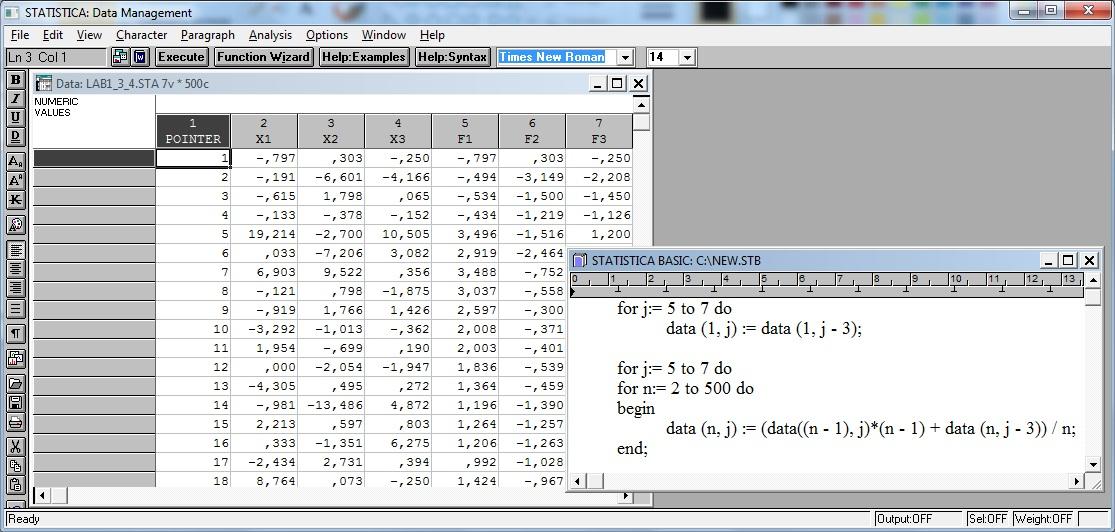
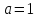
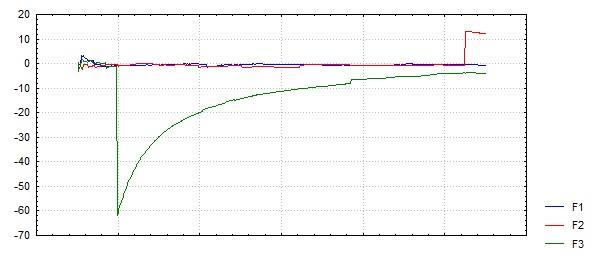
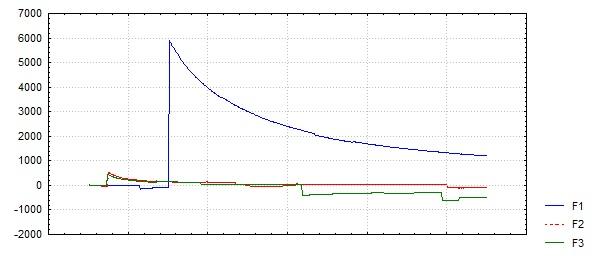
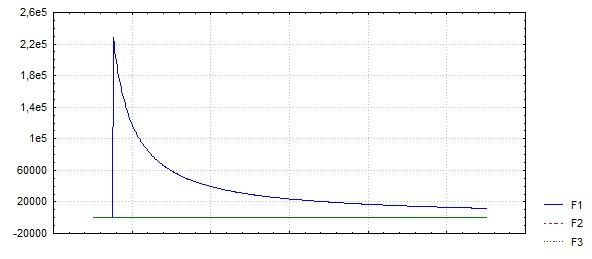
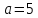
4. Теорема Гливенко – основная теорема статистики.

Пусть x₁, x₂,...,x_n – выборка из 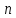независимых наблюдений над случайной величиной X с функцией распределения F(x). Расположим наблюдения в порядке возрастания; получим – вариационный ряд.

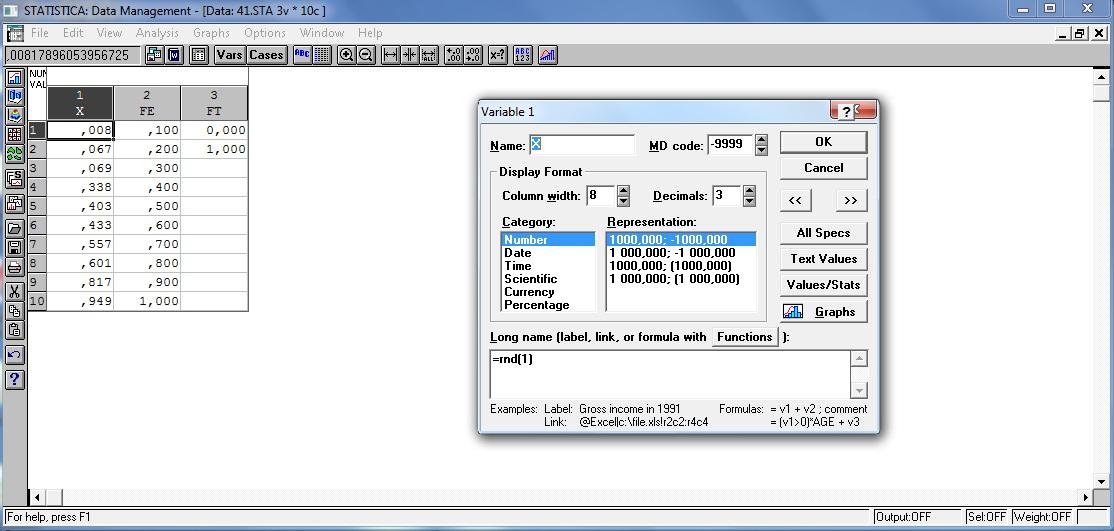
Определим функцию эмпирического распределения

,

где - число тех наблюдений, для которых x_i<x. Ясно, что - ступенчатая функция; это функция распределения, которое получается, если значениям x₁,...,x_n присвоить вероятности, равные 1/n. Ясно, что -функция случайная , так как зависит от наблюдений x₁,...,x_n.

Теорема Гливенко.

при с вероятностью 1.

Проиллюстрируем эту теорему на примерах наблюдений над случайной величиной, распределённой по равномерному на [0,1] закону.

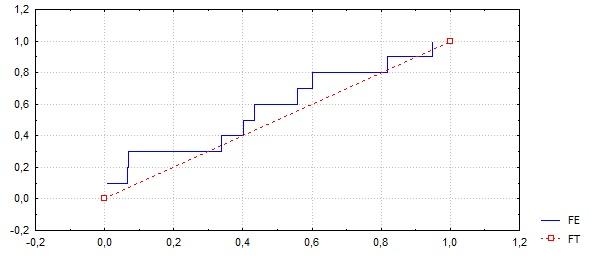
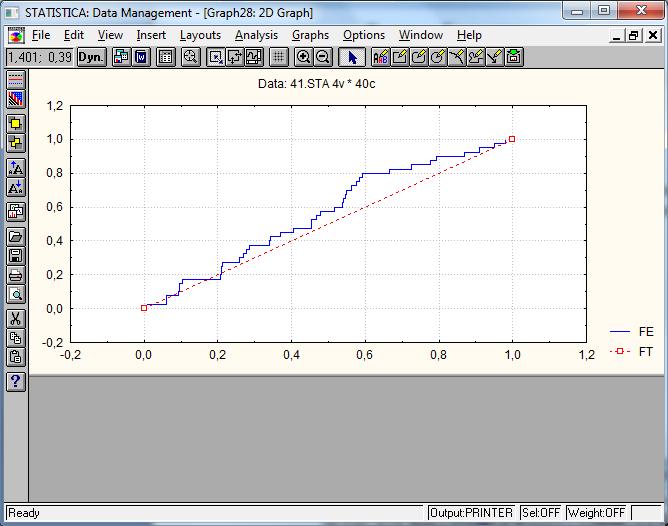
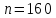
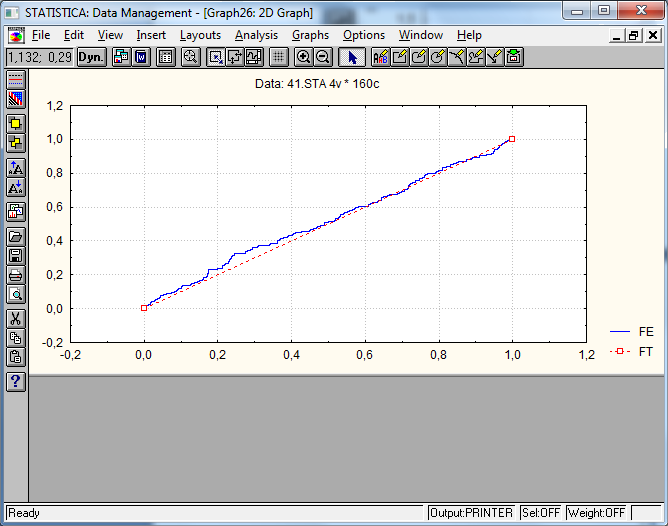
Из проделанного опыта можно сделать вывод, что при увеличении числа наблюдений в выборке функция эмпирического распределения все ближе к теоретической функции распределения.