Тема 5. Доверительные интервалы и границы.
1. Доверительный интервал, нижняя и верхняя доверительные границы.
Всякая точечная оценка сообщает лишь одно значение, которое принимается за приближенное значение оцениваемой величины, при этом полученное значение в большинстве случаев, конечно, не совпадает с истинным значением оцениваемой величины, поэтому в ряде случаев требуется указать интервал, в котором с большой вероятностью находится оцениваемая величина.
Пусть
– наблюдение,
– неизвестный скалярный параметр и
– множество допустимых значений
параметра
.
Определение 5.1.
Пусть
и
– статистики. Интервал
называется доверительным интервалом
для величины
с уровнем доверия (доверительной
вероятностью)
(
),
если:
1)
,
2)
.
Из условия 2) определения 5.1 следует, что
статистики
и
устроены таким образом, что каким бы ни
оказалось значение параметра
величина
«накрывается» интервалом
с вероятностью не меньше чем
.
Определение 5.2.
Статистика
называется верхней доверительной
границей с уровнем доверия (доверительной
вероятностью)
(
),
если:
.
Определение 5.3.
Статистика
называется нижней доверительной
границей с уровнем доверия (доверительной
вероятностью)
(
),
если:
.
Общий метод построения доверительных интервалов основывается на понятии центральной статистики.
Определение 5.4.
Пусть
– наблюдение и случайная величина
зависит как от наблюдения
так и от неизвестной величины
.
Случайная величина
называется центральной статистикой
для величины
,
если:
1) функция распределения известна (то есть никаким образом не зависит от неизвестного параметра ),
2) при всех реализациях наблюдения
одновременно функция
непрерывна и строго монотонна по
(например, при всех
функция
непрерывна и возрастает по
).
Предположим, что некоторым образом
построена центральная статистика для
–
,
поскольку функция распределения
известна (условие 1), то всегда можно
найти числа
и
такие, что:
.
Поскольку функция
непрерывна по
при всех реализациях наблюдения
,
то при каждом
существуют решения
и
системы уравнений (рисунок 5.1):
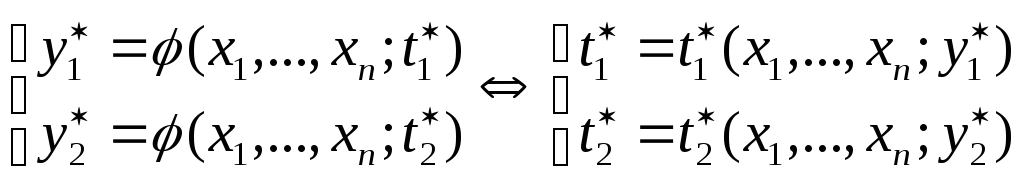
Рисунок 5.1.
Если функция
возрастает по
при всех реализациях наблюдения, тогда
события
и
эквивалентны и вероятности событий
равны, то есть:
.
Пусть статистики
и
,
тогда интервал
является доверительным интервалом для
с уровнем доверия
,
поскольку для всех допустимых значений
параметра
:
,
следовательно,
.
Если функция
убывает по
при всех реализациях наблюдения, тогда
эквивалентны события
и
и равны вероятности:
.
Пусть статистики
и
,
тогда интервал
является доверительным интервалом для
с уровнем доверия
,
поскольку для всех допустимых значений
параметра
:
,
тогда,
Аналогичным образом, с помощью центральной
статистики
могут быть построены доверительные
границы.
2. Доверительный интервал для математического ожидания нормального распределения с известной дисперсией.
Пусть
– выборка из нормального распределения
с неизвестным математическим ожиданием
и известной дисперсией
,
построим доверительный интервал для
математического ожидания
с уровнем доверия
.
Поскольку все величины
выборки имеют нормальное распределение,
то статистика
также имеет нормальное распределение
с параметрами:
,
.
Тогда статистика
:
,
имеет нормальное распределение
не зависящее от неизвестного параметра
и одновременно при всех реализациях
функция
как функция
является непрерывной и убывающей.
Согласно определению
– центральная статистика для
.
Выберем числа
и
так, чтобы выполнялись равенства:
или
,
где
- функция распределения нормальной
случайной величины
.
Для нахождения минимума функции
при условии
воспользуемся методом Лагранжа, с
функцией Лагранжа:
,
которая приводит к системе:
.
У второго уравнения системы
или
,
очевидно, имеется только два решения
и
,
первое решение не удовлетворяет третьему
уравнению системы
,
тогда:
Используя свойство функции нормального
распределения
получим:
.
Таким образом,
есть квантиль уровня
распределения
и
.
Значению
можно придать иную интерпретацию:
,
то есть
является квантилью уровня
распределения
.
Таким образом, получим равенство для
вероятностей:
.
Преобразовывая неравенства, получим:
,
.
Преобразование неравенств фактически является нахождением решения системы:
.
Таким образом, при всяком значении параметра :
,
тогда интервал (
):
,
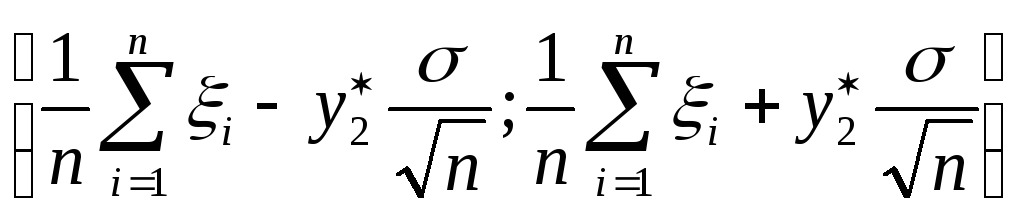где
– является квантилью уровня
распределения
,
является доверительным интервалом для
с уровнем доверия
.