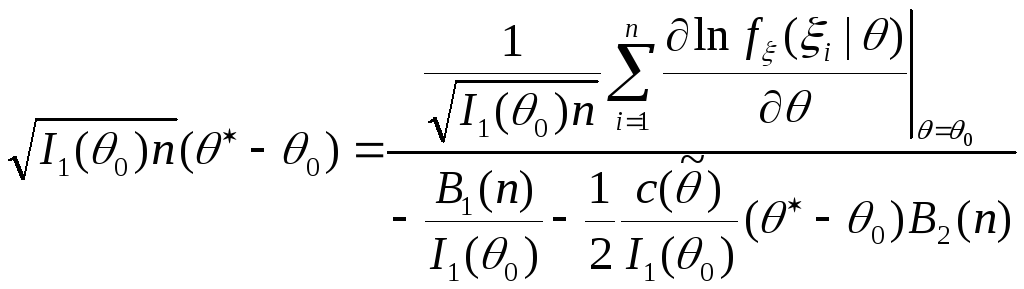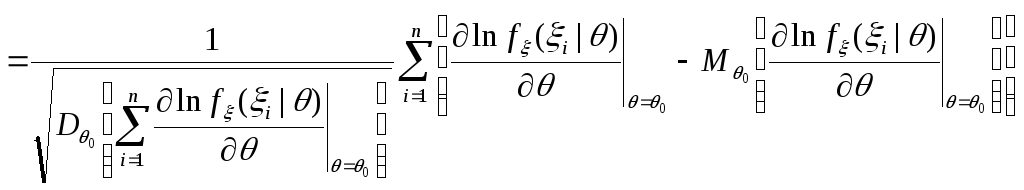Тема 4. Методы построения оценок.
1. Метод моментов.
Пусть
![]() – выборка из распределения
– выборка из распределения
![]() ,
где
,
где
![]() – вектор неизвестных параметров, и
требуется построить оценку величин
– вектор неизвестных параметров, и
требуется построить оценку величин
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Для построения оценок вычислим
![]() моментов
моментов
![]() (
(![]() )
функции распределения
)
функции распределения
![]() ,
в общем случае моменты
,
в общем случае моменты
![]() могут быть как начальные, так и центральные
и не обязательно по порядку. Выражения
для моментов
могут быть как начальные, так и центральные
и не обязательно по порядку. Выражения
для моментов
![]() содержат неизвестные параметры
содержат неизвестные параметры
![]() ,
…,
,
…,
![]() ,
так что каждый момент
,
так что каждый момент
![]() представляет собой функцию
представляет собой функцию
![]() :
:
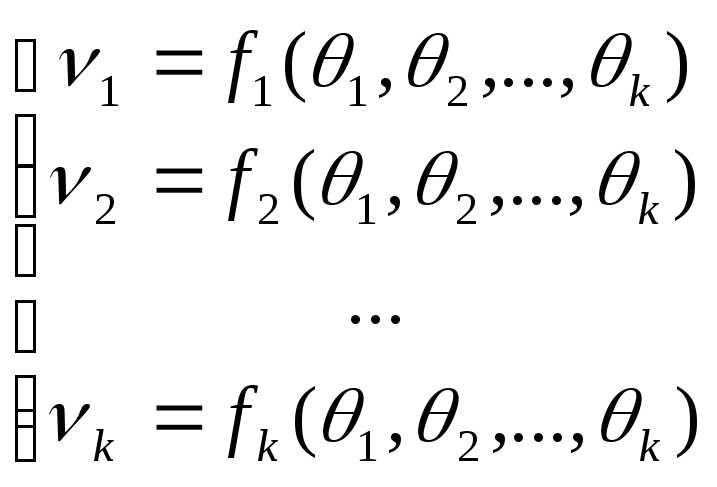 .
.
Пусть представленная система разрешима
относительно неизвестных параметров
![]() ,
…,
,
…,
![]() ,
тогда получим систему выражений:
,
тогда получим систему выражений:
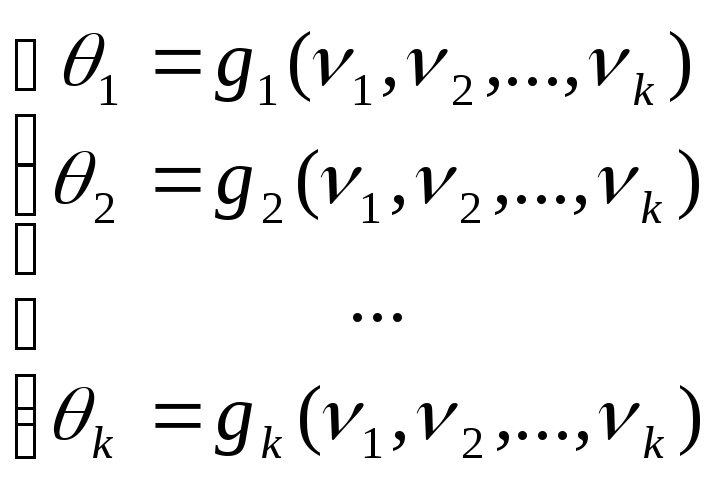
Точные значения моментов
![]() неизвестны, но известны оценки моментов
неизвестны, но известны оценки моментов
![]() ,
полученные на основе выборки
,
полученные на основе выборки
![]() .
Используя оценки
.
Используя оценки
![]() ,
получим оценки неизвестных параметров:
,
получим оценки неизвестных параметров:
|
|
(4.1) |
Определение 4.1.
Оценки
![]() ,
…,
,
…,
![]() в системе (4.1) называются оценками,
полученными по методу моментов
(кратко, моментными оценками).
в системе (4.1) называются оценками,
полученными по методу моментов
(кратко, моментными оценками).
Моментные оценки
![]() ,
…,
,
…,
![]() в общем случае не обладают свойством
несмещенности (тем не менее, в некоторых
частных случаях моментные оценки
оказываются несмещенными).
в общем случае не обладают свойством
несмещенности (тем не менее, в некоторых
частных случаях моментные оценки
оказываются несмещенными).
Если функция
![]() (
(![]() )
непрерывна в точке
)
непрерывна в точке
![]() ,
то моментная оценка
,
то моментная оценка
![]() является состоятельной. Действительно,
оценки начальных и центральных моментов
является состоятельной. Действительно,
оценки начальных и центральных моментов
![]() являются состоятельными, откуда в силу
свойства сходимости по вероятности,
непрерывная функция
являются состоятельными, откуда в силу
свойства сходимости по вероятности,
непрерывная функция
![]() от оценок
от оценок
![]() ,
имеющих пределом по вероятности
,
имеющих пределом по вероятности
![]() ,
сходится по вероятности к величине
,
сходится по вероятности к величине
![]() ,
таким образом:
,
таким образом:
![]() ,
,
что означает состоятельность оценоки
![]() .
.
Если в качестве
![]() используются первые
используются первые
![]() начальных моментов
начальных моментов
![]() функции распределения
функции распределения
![]() ,
функции
,
функции
![]() ,
…,
,
…,
![]() непрерывно дифференцируемы и функция
распределения
непрерывно дифференцируемы и функция
распределения
![]() имеет
имеет
![]() моментов, то моментные оценки
моментов, то моментные оценки
![]() имеют асимптотически нормальное
распределение:
имеют асимптотически нормальное
распределение:
 ,
,
где
![]() – вектор начальных моментов.
– вектор начальных моментов.
Моментные оценки в большом количестве случаев не являются эффективными и оптимальными, тем не менее, метод построения оценок оказывается простым и сами выражения для моментных оценок (4.1), как правило, оказываются простыми для вычисления.
2. Метод максимального правдоподобия.
Пусть
![]() – наблюдение (не обязательно выборка)
и
– наблюдение (не обязательно выборка)
и
![]() – плотность вероятности (или вероятность
в дискретном случае) вектора
– плотность вероятности (или вероятность
в дискретном случае) вектора
![]() ,
которая зависит от неизвестного вектора
параметров
,
которая зависит от неизвестного вектора
параметров
![]() .
В результате проведения эксперимента
будет получен числовой вектор
.
В результате проведения эксперимента
будет получен числовой вектор
![]() ,
подставляя который в функцию
,
подставляя который в функцию
![]() ,
получим функцию, зависящую только от
вектора
,
получим функцию, зависящую только от
вектора
![]() (функцию правдоподобия – определение
3.1). При одних значениях параметра
(функцию правдоподобия – определение
3.1). При одних значениях параметра
![]() значение функции правдоподобия
значение функции правдоподобия
![]() оказывается мало, при других значениях
– велико. Поскольку значение функция
правдоподобия
оказывается мало, при других значениях
– велико. Поскольку значение функция
правдоподобия
![]() отражает вероятность получения заданного
вектора
отражает вероятность получения заданного
вектора
![]() ,
то волне естественно выбрать параметр
,
то волне естественно выбрать параметр
![]() так, чтобы вероятность получения
наблюдаемого значения
так, чтобы вероятность получения
наблюдаемого значения
![]() оказалось бы наибольшей.
оказалось бы наибольшей.
Определение 4.2.
Пусть
![]() – наблюдение и
– наблюдение и
![]() – функция правдоподобия. Оценка
– функция правдоподобия. Оценка
![]() ,
доставляющая наибольшее значение
функции правдоподобия при каждом
наблюдении
,
доставляющая наибольшее значение
функции правдоподобия при каждом
наблюдении
![]() ,
называется оценкой максимального
правдоподобия (кратко, МП-оценкой):
,
называется оценкой максимального
правдоподобия (кратко, МП-оценкой):
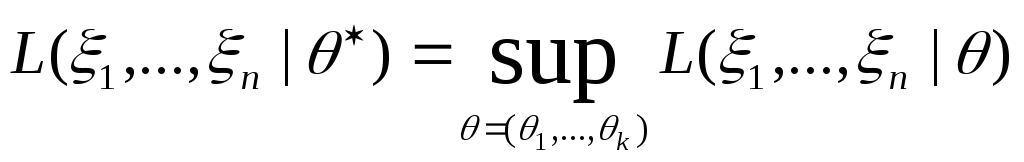 .
.
Определение 4.2 следует понимать в
следующем смысле: при каждом фиксированном
элементарном событии
![]() ,
случайные величины наблюдения
,
случайные величины наблюдения
![]() ,
…,
,
…,
![]() принимают определенные числовые значения
принимают определенные числовые значения
![]() ,
а само наблюдение
,
а само наблюдение
![]() при фиксированном
при фиксированном
![]() становится числовым вектором
становится числовым вектором
![]() .
Для заданного вектора
.
Для заданного вектора
![]() согласно определению 4.2 вычисляется
значение МП-оценки
согласно определению 4.2 вычисляется
значение МП-оценки
![]() :
:
 .
.
Тем самым для каждого
![]() задан способ вычисления МП-оценки
задан способ вычисления МП-оценки
![]() ,
который и определяет функцию наблюдения
,
который и определяет функцию наблюдения
![]() .
Таким образом, МП-оценка как функция
наблюдения является статистикой.
.
Таким образом, МП-оценка как функция
наблюдения является статистикой.
Если при каждой реализации вектора
![]() наибольшее значение функции правдоподобия
соответствует внутренней точке множества
допустимых значений параметра
наибольшее значение функции правдоподобия
соответствует внутренней точке множества
допустимых значений параметра
![]() и функция правдоподобия
и функция правдоподобия
![]() дифференцируема по параметру, то из
необходимого условия экстремума следует
равенство частных производных функции
правдоподобия
дифференцируема по параметру, то из
необходимого условия экстремума следует
равенство частных производных функции
правдоподобия
![]() нулю в точке МП-оценки
нулю в точке МП-оценки
![]() :
:
![]() ,
,
![]() .
.
Решение приведенной системы не всегда
оказывается удобным, поэтому при
выполнении определенных условий задачу
нахождения наибольшего значения функции
правдоподобия
![]() заменяют задачей нахождения наибольшего
значения логарифма функции правдоподобия
заменяют задачей нахождения наибольшего
значения логарифма функции правдоподобия
![]() ,
поскольку логарифм функция монотонно
возрастающая (и, следовательно, наибольшему
значению логарифма функции правдоподобия
будет соответствовать наибольшее
значение самой функции правдоподобия):
,
поскольку логарифм функция монотонно
возрастающая (и, следовательно, наибольшему
значению логарифма функции правдоподобия
будет соответствовать наибольшее
значение самой функции правдоподобия):
![]() ,
,
![]() .
.
В случае скалярного параметра
![]() представленное уравнение имеет название
уравнения правдоподобия.
представленное уравнение имеет название
уравнения правдоподобия.
Утверждение 4.3.
Пусть выполнены условия теоремы 3.4,
![]() – наблюдение и статистика
– наблюдение и статистика
![]() является эффективной оценкой параметра
является эффективной оценкой параметра
![]() ,
тогда
,
тогда
![]() является МП-оценкой параметра
является МП-оценкой параметра
![]() .
.
Доказательство:
Поскольку
![]() – эффективная оценка и выполнены условия
теоремы 3.4, то в силу следствия 3.5
имеет место равенство:
– эффективная оценка и выполнены условия
теоремы 3.4, то в силу следствия 3.5
имеет место равенство:
![]() ,
,
![]() .
.
Пусть
![]() – МП-оценка, тогда при всех реализациях
вектора
– МП-оценка, тогда при всех реализациях
вектора
![]() :
:
![]() ,
,
отсюда при всех реализациях векторах
![]() :
:
![]() ,
,
тогда при всех реализациях вектора
![]() :
:
![]() ,
,
![]() .
.
Таким образом, оценки
![]() и
и
![]() совпадают.
совпадают.
Утверждение доказано.
Утверждение 4.4.
Пусть
![]() – наблюдение и
– наблюдение и
![]() – статистика достаточная для параметра
– статистика достаточная для параметра
![]() ,
тогда МП-оценка параметра
,
тогда МП-оценка параметра
![]() является функцией достаточной статистики
является функцией достаточной статистики
![]() .
.
Доказательство:
Поскольку
![]() – достаточная для параметра
– достаточная для параметра
![]() статистика, то по критерию факторизации
(теорема 3.12) для
функции правдоподобия
статистика, то по критерию факторизации
(теорема 3.12) для
функции правдоподобия
![]() имеется разложение:
имеется разложение:
![]()
В соответствии с определением МП-оценка
доставляет наибольшее значение функции
правдоподобия
![]() :
:
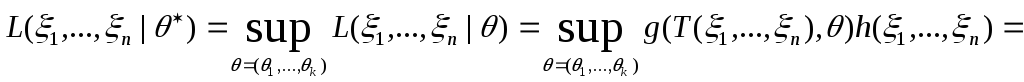
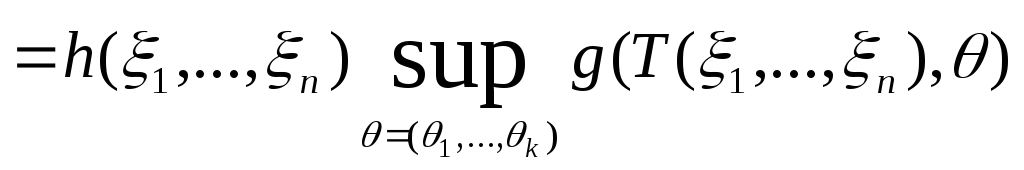 .
.
Значение параметра
![]() ,
соответствующее наибольшему значению
функции
,
соответствующее наибольшему значению
функции
![]() ,
будет зависеть от
,
будет зависеть от
![]() ,
…,
,
…,
![]() только через значения статистики
только через значения статистики
![]() ,
поэтому МП-оценка
,
поэтому МП-оценка
![]() будет функцией статистики
будет функцией статистики
![]() :
:
![]() .
.
Утверждение доказано.
Определение 4.5.
Статистика
![]() ,
являющаяся оценкой неизвестного
параметра
,
являющаяся оценкой неизвестного
параметра
![]() ,
называется асимптотически эффективной,
если при каждом допустимом значении
,
называется асимптотически эффективной,
если при каждом допустимом значении
![]() :
:
![]() ,
,
где
![]() – дисперсия оценки
– дисперсия оценки
![]() ,
,
![]() – нижняя граница дисперсии из неравенства
Рао-Крамера,
– нижняя граница дисперсии из неравенства
Рао-Крамера,
![]() – информация Фишера о параметре
– информация Фишера о параметре
![]() ,
содержащаяся в наблюдении
,
содержащаяся в наблюдении
![]() .
.
Определение 4.6.
Статистика
![]() называется асимптотически нормальной
с параметрами
называется асимптотически нормальной
с параметрами
![]() и
и
![]() :
:
![]() при
при
![]() ,
,
если при каждом
![]() :
:
![]() ,
,
где
![]() – функция распределения
– функция распределения
![]() ,
,
![]() – функция Лапласа (функция распределения
нормальной случайной величины с
математическим ожиданием 0 и дисперсией
1).
– функция Лапласа (функция распределения
нормальной случайной величины с
математическим ожиданием 0 и дисперсией
1).
Теорема 4.7. (асимптотические свойства МП-оценок)
Пусть
![]() – выборка из распределения с плотностью
вероятностью
– выборка из распределения с плотностью
вероятностью
![]() ,
зависящей от скалярного параметра
,
зависящей от скалярного параметра
![]() ,
,
![]() – множество допустимых значений
параметра,
– множество допустимых значений
параметра,
![]() – истинное значение параметра,
– истинное значение параметра,
![]() – МП-оценка параметра
– МП-оценка параметра
![]() .
.
Если,
1) при каждом
![]() и почти всех
и почти всех
![]() существуют производные
существуют производные
![]() ,
,
![]() и
и
![]() ;
;
2) при каждом
![]() и почти всех
и почти всех
![]() :
:
![]() и
и
![]() ,
причем существуют интегралы
,
причем существуют интегралы
![]() и
и
![]() ;
;
3) при каждом
![]() и почти всех
и почти всех
![]() :
:
![]() и существует единая постоянная
и существует единая постоянная
![]() такая, что для всех
такая, что для всех
![]() :
:
![]() .
.
4) при каждом
![]() конечен и положителен интеграл:
конечен и положителен интеграл:
![]()
Тогда,
1) МП-оценка
![]() состоятельна, то есть
состоятельна, то есть
![]() при
при
![]() ;
;
2) МП-оценка
![]() является асимптотически нормальной;
является асимптотически нормальной;
3) МП-оценка
![]() асимптотически эффективная;
асимптотически эффективная;
Доказательство:
1) Пусть
![]() – функция правдоподобия выборки
– функция правдоподобия выборки
![]() ,
поскольку
,
поскольку
![]() – выборка из распределения с плотностью
вероятности
– выборка из распределения с плотностью
вероятности
![]() ,
то в силу независимости и одинаковости
распределений случайных величин
,
то в силу независимости и одинаковости
распределений случайных величин
![]() (
(![]() )
для функции правдоподобия получим
выражение:
)
для функции правдоподобия получим
выражение:
![]() ,
,
откуда,
|
|
(4.2) |
Разложим функцию
![]() в точке истинного значения параметра
в точке истинного значения параметра
![]() :
:
![]() ,
,
где
![]() – некоторая точка между
– некоторая точка между
![]() и
и
![]() .
Поскольку по условию
.
Поскольку по условию
![]() ,
то
,
то
![]() ,
где
,
где
![]() ,
тогда:
,
тогда:
![]()
Подставляя разложение в (4.2), получим:
![]()
![]() .
.
Разделим левую и правую части на
![]() :
:
|
|
(4.3) |
Вычислим математическое ожидание
случайных величин
![]() :
:
![]()
![]() ,
,
где дифференцирование по параметру
![]() можно вынести за интеграл в силу условий
1) и 2) теоремы. Поскольку случайные
величины
можно вынести за интеграл в силу условий
1) и 2) теоремы. Поскольку случайные
величины
![]() независимы и имеют одинаковое
распределение, то таковыми же являются
случайные величины
независимы и имеют одинаковое
распределение, то таковыми же являются
случайные величины
![]() и поскольку математические ожидания
случайных величин:
и поскольку математические ожидания
случайных величин:
![]() ,
,
то к этим случайным величинам применима теорема Хинчина, согласно которой имеет место сходимость по вероятности:
|
|
(4.4) |
Вычислим математическое ожидание
случайных величин
![]() :
:
![]()
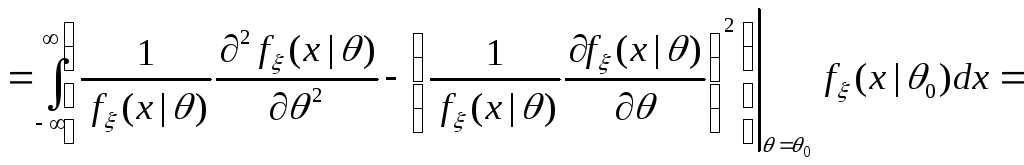
![]()
![]()
![]()
![]() ,
,
где
![]() – информация Фишера, содержащаяся в
наблюдении, состоящем из одной случайной
величины
– информация Фишера, содержащаяся в
наблюдении, состоящем из одной случайной
величины
![]() .
Случайные величины
.
Случайные величины
![]() независимы и имеют одинаковое
распределение, поскольку случайные
величины
независимы и имеют одинаковое
распределение, поскольку случайные
величины
![]() ,
…,
,
…,
![]() образуют выборку. Математические
ожидания случайных величин
образуют выборку. Математические
ожидания случайных величин
![]() существуют и все равны
существуют и все равны
![]() ,
отсюда по теореме Хинчина имеет место
сходимость по вероятности:
,
отсюда по теореме Хинчина имеет место
сходимость по вероятности:
|
|
(4.5) |
Случайные величины
![]() (
(![]() )
независимы и имеют одинаковое
распределение, поскольку случайные
величины
)
независимы и имеют одинаковое
распределение, поскольку случайные
величины
![]() ,
…,
,
…,
![]() образуют выборку, математическое
ожидание
образуют выборку, математическое
ожидание
![]() ,
согласно условию 4 теоремы. Отсюда, к
случайным величинам
,
согласно условию 4 теоремы. Отсюда, к
случайным величинам
![]() применима теорема Хинчина, поэтому
имеет место сходимость по вероятности:
применима теорема Хинчина, поэтому
имеет место сходимость по вероятности:
|
|
(4.6) |
Выберем произвольным образом и зафиксируем
числа
![]() и
и
![]() ,
представим соотношение (4.3) в следующем
виде:
,
представим соотношение (4.3) в следующем
виде:
|
|
(4.7) |
где
![]() ,
,
![]() и
и
![]() .
.
Согласно (4.4)
![]() сходится по вероятности к нулю, поэтому
найдется
сходится по вероятности к нулю, поэтому
найдется
![]() такое, что при каждом
такое, что при каждом![]() :
:
![]() ,
,
![]()
Пусть событие
![]() ,
тогда
,
тогда
![]() .
.
Согласно (4.5)
![]() сходится по вероятности к
сходится по вероятности к
![]() ,
поэтому найдется
,
поэтому найдется
![]() такое, что при каждом
такое, что при каждом
![]() :
:
![]() ,
,
![]()
Легко видеть, что событие, стоящее справа можно представить как объединение двух событий:
![]()
![]() .
.
Пусть
![]() ,
тогда
,
тогда
![]() ,
откуда
,
откуда
![]() .
.
Согласно (4.6)
![]() сходится по вероятности к
сходится по вероятности к
![]() ,
поэтому найдется
,
поэтому найдется
![]() такое, что при каждом
такое, что при каждом
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Пусть
![]() ,
легко видеть, что
,
легко видеть, что
![]() ,
,
то есть событие
![]() ,
тогда
,
тогда
![]() .
.
Пусть![]() и
и
![]() заключается в том, что выполнены все
три неравенства, тогда дополнительное
событие
заключается в том, что выполнены все
три неравенства, тогда дополнительное
событие
![]() состоит из тех элементарных событий
состоит из тех элементарных событий
![]() ,
при которых не выполнено хотя бы одно
неравенство. Поскольку все элементарные
события
,
при которых не выполнено хотя бы одно
неравенство. Поскольку все элементарные
события
![]() ,
при которых выполнено неравенство
,
при которых выполнено неравенство
![]() ,
заключены во множестве
,
заключены во множестве
![]() ,
то
,
то
![]() .
Аналогично,
.
Аналогично,
![]() и
и
![]() ,
тогда:
,
тогда:
![]()
и следовательно,
![]() ,
,
тогда,
![]()
При
![]() справедливы неравенства:
справедливы неравенства:
![]() ,
,
![]() ,
,
![]() ,
,
причем согласно условию 4 теоремы:
![]() ,
,
тогда, при
![]() :
:
|
|
(4.8) |
Выберем произвольным образом и зафиксируем
![]() ,
рассмотрим
,
рассмотрим
![]() -окрестность
точки
-окрестность
точки
![]() ,
пусть
,
пусть
![]() ,
тогда из (4.7):
,
тогда из (4.7):
![]()
Поскольку выполнены неравенства (4.8) и
![]() ,
то
,
то
![]() .
.
Легко видеть, что
![]() и
и
![]() ,
причем если
,
причем если
 ,
то:
,
то:
![]() ,
,
то есть при
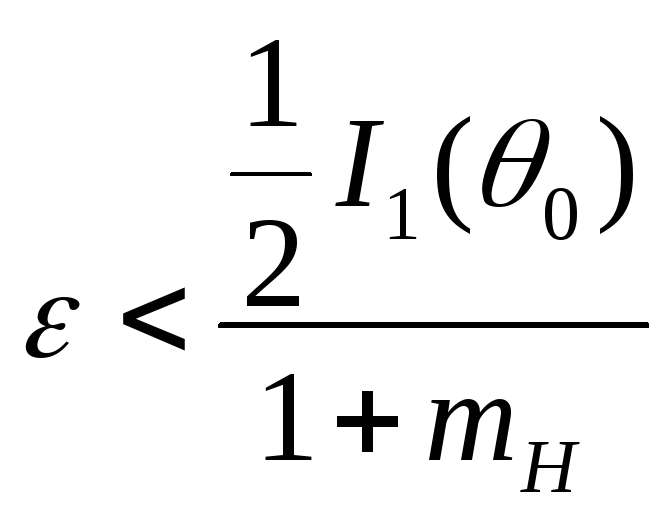 положительное слагаемое
положительное слагаемое
![]() больше, чем модуль отрицательного
слагаемого
больше, чем модуль отрицательного
слагаемого
![]() ,
тогда, очевидно,
,
тогда, очевидно,
![]() .
.
Пусть теперь
![]() ,
тогда из (4.7) получим:
,
тогда из (4.7) получим:
![]()
Поскольку выполнены неравенства (4.8) и
![]() ,
то:
,
то:
![]()
Очевидно, что
![]() и
и
![]() ,
а при
,
а при
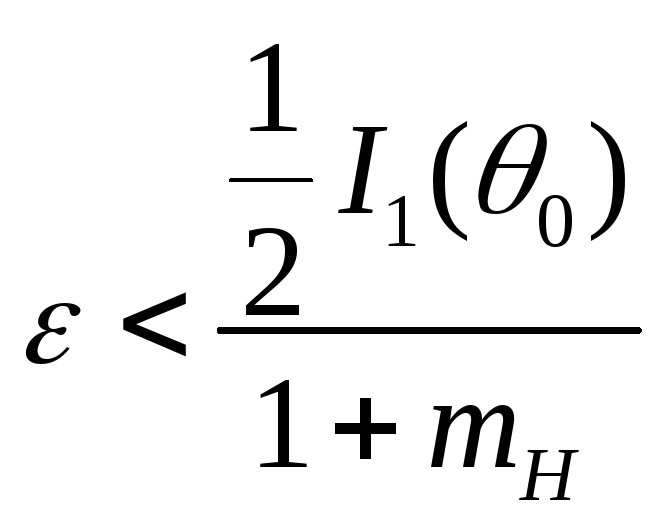 как и ранее
как и ранее
![]() ,
то есть модуль отрицательного слагаемого
,
то есть модуль отрицательного слагаемого
![]() больше положительного слагаемого
больше положительного слагаемого
![]() ,
откуда следует, что:
,
откуда следует, что:
![]() .
.
Таким образом, при
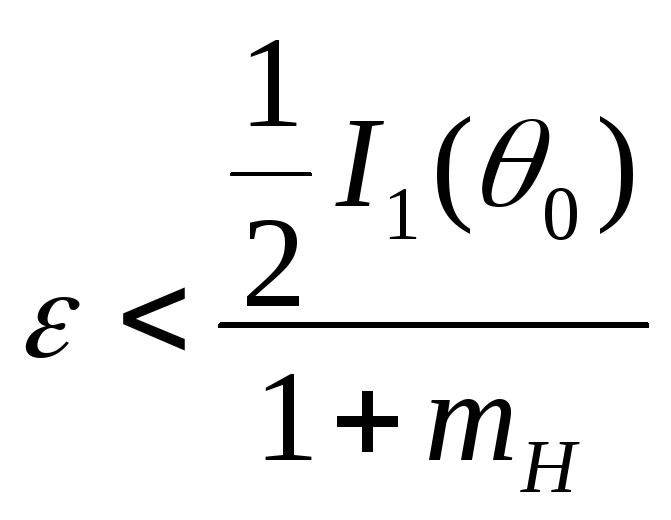 в
в
![]() -окрестности
-окрестности
![]() функция
функция
![]() ,
как функция параметра
,
как функция параметра
![]() ,
принимает как положительные так и
отрицательные значения. Поскольку
существует производная
,
принимает как положительные так и
отрицательные значения. Поскольку
существует производная
![]() ,
то функция
,
то функция
![]() ,
как функция параметра
,
как функция параметра
![]() ,
является непрерывной, тогда из (4.2)
функция
,
является непрерывной, тогда из (4.2)
функция
![]() так же непрерывна, как сумма непрерывных
функций. По известной теореме анализа,
для непрерывной функции
так же непрерывна, как сумма непрерывных
функций. По известной теореме анализа,
для непрерывной функции
![]() ,
принимающей в
,
принимающей в
![]() -окрестности
-окрестности
![]() как положительные так и отрицательные
значения найдется точка
как положительные так и отрицательные
значения найдется точка
![]() в которой функция
в которой функция
![]() принимает значение ноль:
принимает значение ноль:
![]() ,
,
причем сама точка
![]() находится внутри
находится внутри
![]() -окрестности
точки
-окрестности
точки
![]() ,
,
![]() .
.
Таким образом, для всякого
![]() и достаточно малого
и достаточно малого
![]() существует решение уравнения правдоподобия
– точка
существует решение уравнения правдоподобия
– точка
![]() ,
причем такое, что
,
причем такое, что
![]() ,
причем
,
причем
![]() .
.
Заметим, что
![]() есть множество только некоторых таких
есть множество только некоторых таких
![]() ,
при которых существует решение уравнения
правдоподобия
,
при которых существует решение уравнения
правдоподобия
![]() и
и
![]() ,
возможно есть и другие такие
,
возможно есть и другие такие
![]() ,
не входящие во множество
,
не входящие во множество
![]() .
Пусть теперь
.
Пусть теперь
![]() – множество всех
– множество всех
![]() ,
при которых существует решение
,
при которых существует решение
![]() уравнения правдоподобия при заданном
уравнения правдоподобия при заданном
![]() и
и
![]() ,
тогда, очевидно,
,
тогда, очевидно,
![]() и следовательно
и следовательно
![]() .
.
Итого, для произвольного
![]() и достаточно малого произвольного
и достаточно малого произвольного
![]() найдется число
найдется число
![]() такое, что для каждого
такое, что для каждого
![]() множество
множество
![]() всех элементарных событий
всех элементарных событий
![]() ,
при которых существует решение уравнения
правдоподобия
,
при которых существует решение уравнения
правдоподобия
![]() ,
такое что
,
такое что
![]() ,
имеет вероятность больше, чем
,
имеет вероятность больше, чем
![]() :
:
![]() ,
,
отсюда по определению сходимости по
вероятности МП-оценка
![]() сходится по вероятности к
сходится по вероятности к
![]() и по определению состоятельности
МП-оценка
и по определению состоятельности
МП-оценка
![]() является состоятельной.
является состоятельной.
2) Пусть
![]() – МП-оценка параметра
– МП-оценка параметра
![]() ,
тогда
,
тогда
![]() является решением уравнения правдоподобия:
является решением уравнения правдоподобия:
![]() .
.
Отсюда с учетом (4.3):
![]() ,
,
где
![]() и
и
![]() ,
тогда:
,
тогда:
![]() ,
,
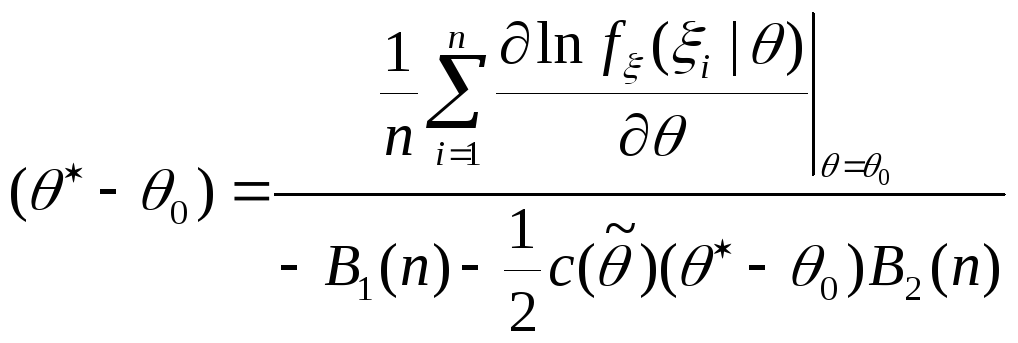 ,
,
 ,
,
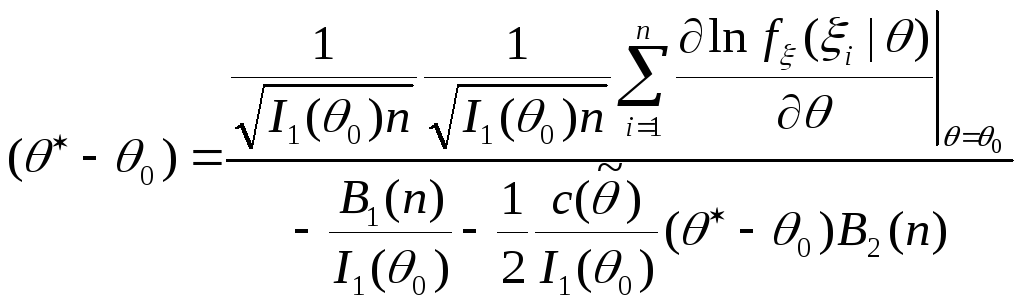 ,
,
|
|
(4.9) |
Поскольку случайные величины
![]() ,
…,
,
…,
![]() образуют выборку, то они совместно
независимы и имеют одинаковую функцию
распределения, отсюда следует, что
случайные величины
образуют выборку, то они совместно
независимы и имеют одинаковую функцию
распределения, отсюда следует, что
случайные величины
![]() так же совместно независимы и имеют
одинаковую функцию распределения,
причем как было показано ранее
так же совместно независимы и имеют
одинаковую функцию распределения,
причем как было показано ранее
![]() .
Заметим, что
.
Заметим, что
![]() ,
отсюда в силу совместной независимости
,
отсюда в силу совместной независимости
![]() :
:
![]() .
.
Таким образом, числитель правой части (4.9) можно представить в виде:
|
|
(4.10) |
Случайные величины
![]() совместно независимы, имеют одинаковое
распределение, конечное математическое
ожидание 0 и конечную дисперсию
совместно независимы, имеют одинаковое
распределение, конечное математическое
ожидание 0 и конечную дисперсию
![]() (условие 4 теоремы), поэтому к ним применима
центральная предельная теорема, согласно
которой правая часть (4.10) имеет
асимптотически нормальное распределение
с параметрами 0 и
(условие 4 теоремы), поэтому к ним применима
центральная предельная теорема, согласно
которой правая часть (4.10) имеет
асимптотически нормальное распределение
с параметрами 0 и
![]() ,
и следовательно числитель правой части
(4.9):
,
и следовательно числитель правой части
(4.9):
![]() ,
при
,
при
![]() .
.
В знаменателе правой части (4.9) случайная
величина
![]() сходится по вероятности к
сходится по вероятности к
![]() (соотношение (4.5)), поэтому по свойству
сходимости по вероятности случайная
величина
(соотношение (4.5)), поэтому по свойству
сходимости по вероятности случайная
величина
![]() сходится по вероятности к 1:
сходится по вероятности к 1:
|
|
(4.11а) |
Случайная величина
![]() сходится по вероятности к
сходится по вероятности к
![]() (соотношение (4.6)), МП-оценка
(соотношение (4.6)), МП-оценка
![]() состоятельна (согласно пункту 1
доказательства), поэтому
состоятельна (согласно пункту 1
доказательства), поэтому
![]() сходится по вероятности к
сходится по вероятности к
![]() ,
следовательно разность
,
следовательно разность
![]() сходится по вероятности к 0, тогда по
свойству сходимости по вероятности
произведение
сходится по вероятности к 0, тогда по
свойству сходимости по вероятности
произведение
![]() сходится по вероятности к
сходится по вероятности к
![]() .
Постоянная
.
Постоянная
![]() конечна, поэтому по свойству сходимости
по вероятности произведение
конечна, поэтому по свойству сходимости
по вероятности произведение
![]() сходится по вероятности к
сходится по вероятности к
![]() :
:
|
|
(4.11б) |
Из (4.11а) и (4.11б) следует сходимость по вероятности знаменателя правой части (4.9) к 1:
![]() ,
при
,
при
![]() .
.
Таким образом, числитель правой части (4.9) имеет асимптотически нормальное распределение с параметрами 0 и 1, а знаменатель сходится по вероятности к 1, по свойству сходимости по вероятности правая часть (4.9) имеет асимптотически нормальное распределение с параметрами 0 и 1, тогда и левая часть (4.9) имеет асимптотически нормальное распределение с параметрами 0 и 1:
![]() ,
при
,
при
![]() .
.
Отсюда следует, что
![]() имеет асимптотически нормальное
распределение с параметрами
имеет асимптотически нормальное
распределение с параметрами
![]() и
и
![]() :
:
|
|
(4.12) |
3) Поскольку
![]() ,
…,
,
…,
![]() образуют выборку, то информация Фишера
образуют выборку, то информация Фишера
![]() о параметре
о параметре
![]() ,
содержащейся в выборке
,
содержащейся в выборке
![]() ,
согласно утверждению 3.8:
,
согласно утверждению 3.8:
![]() .
.
Поскольку оценивается сам параметр
![]() ,
то в неравенстве Рао-Крамера
,
то в неравенстве Рао-Крамера
![]() ,
тогда
,
тогда
![]() и, следовательно, нижняя граница дисперсии
и, следовательно, нижняя граница дисперсии
![]() в неравенстве Рао-Крамера:
в неравенстве Рао-Крамера:
![]() .
.
Поскольку в пунктах 1 и 2 доказательства
не накладывалось никаких ограничений
на
![]() ,
то каким бы ни оказалось истинное
значение параметра
,
то каким бы ни оказалось истинное
значение параметра
![]() имеет место асимптотическая нормальность
МП-оценки
имеет место асимптотическая нормальность
МП-оценки
![]() ,
то есть при любом значении параметра
,
то есть при любом значении параметра
![]() из (4.12) получим:
из (4.12) получим:
![]() ,
при
,
при
![]() .
.
Отсюда следует, что дисперсия МП-оценки
![]() стремиться к
стремиться к
![]() при
при
![]() :
:
![]() ,
,
то есть МП-оценка оценка
![]() по определению асимптотически эффективная.
по определению асимптотически эффективная.
Теорема доказана.