
- •Тема 5. Доверительные интервалы и границы.
- •1. Доверительный интервал, нижняя и верхняя доверительные границы.
- •2. Доверительный интервал для математического ожидания нормального распределения с известной дисперсией.
- •3. Доверительный интервал для дисперсии нормального распределения с известным математическим ожиданием.
- •4. Доверительный интервал для дисперсии нормального распределения с неизвестным математическим ожиданием.
- •5. Доверительный интервал для математического ожидания нормального распределения с неизвестной дисперсией.
- •6. Метод построения центральной статистики.
- •7. Построение доверительных интервалов на основе асимптотической нормальности. Доверительный интервал для вероятности события.
- •8. Доверительный интервал для коэффициента корреляции двумерного нормального распределения с неизвестными математическими ожиданиями и дисперсиями.
5. Доверительный интервал для математического ожидания нормального распределения с неизвестной дисперсией.
Пусть
![]() – выборка из нормального распределения
с неизвестным математическим ожиданием
– выборка из нормального распределения
с неизвестным математическим ожиданием![]() и неизвестной дисперсией
и неизвестной дисперсией![]() ,
построим доверительный интервал для
,
построим доверительный интервал для![]() с уровнем доверия
с уровнем доверия![]() .
.
Рассмотрим статистику
![]() :
:
|
|
(5.4) |
![]() ,
,![]() .
.
Заметим, что:
1)
 ,
поскольку все величины
,
поскольку все величины![]() имеют нормальное распределение;
имеют нормальное распределение;
2)
 и
и![]() независимы, поскольку в силу теоремы
5.5 статистики
независимы, поскольку в силу теоремы
5.5 статистики![]() и
и![]() независимы;
независимы;
3)
![]() имеет распределение
имеет распределение![]() в силу теоремы 5.5.
в силу теоремы 5.5.
Из 1)-3) следует, что статистика
![]() имеет распределение Стьюдента с
имеет распределение Стьюдента с![]() степенью свободы
степенью свободы![]() .
Кроме того, при всех реализациях выборки
.
Кроме того, при всех реализациях выборки![]() функция
функция![]() как функция
как функция![]() является непрерывной и убывающей,
следовательно, случайная величина
является непрерывной и убывающей,
следовательно, случайная величина![]() является центральной статистикой для
является центральной статистикой для![]() .
.
Пусть
![]() и
и![]() – квантили уровней
– квантили уровней![]() и
и![]() распределения
распределения![]() ,
тогда:
,
тогда:
![]() ,
,
 ,
,
![]() .
.
Поскольку распределение Стьюдента
![]() является симметричным относительно
нуля, то для функции распределения
является симметричным относительно
нуля, то для функции распределения![]() справедливо равенство:
справедливо равенство:
![]() .
.
Отсюда следует, что
![]() ,
действительно:
,
действительно:
![]() .
.
Таким образом,
![]()
и следовательно интервал,
![]() ,
,
в котором
![]() ,
,![]() и
и![]() – квантиль уровня
– квантиль уровня![]() распределения Стьюдента с
распределения Стьюдента с![]() степенью свободы, является доверительным
интервалом для
степенью свободы, является доверительным
интервалом для![]() с уровнем доверия
с уровнем доверия![]() .
.
6. Метод построения центральной статистики.
Пусть
![]() – случайная величина с непрерывной и
возрастающей по
– случайная величина с непрерывной и
возрастающей по![]() функцией распределения
функцией распределения![]() ,
возможно зависящей от параметра
,
возможно зависящей от параметра![]() .
Рассмотрим случайную величину
.
Рассмотрим случайную величину![]() ,
легко видеть, что функция распределения
,
легко видеть, что функция распределения![]() случайной величины
случайной величины![]() :
:
 ,
,
где обратная функция
![]() существует, поскольку функция распределения
существует, поскольку функция распределения![]() непрерывна и возрастает. Заметим, что
если
непрерывна и возрастает. Заметим, что
если![]() ,
то:
,
то:
![]() ,
,
таким образом,
 ,
,
и следовательно случайная величина
![]() имеет равномерное распределение
имеет равномерное распределение![]() ,
не зависящее от параметра
,
не зависящее от параметра![]() .
.
Пусть
![]() – наблюдение и
– наблюдение и![]() – статистика (например, оценка или
достаточная статистика), функция
распределения которой
– статистика (например, оценка или
достаточная статистика), функция
распределения которой![]() непрерывна и возрастает по
непрерывна и возрастает по![]() и кроме того известна полностью либо
известна с точностью до значения
параметра
и кроме того известна полностью либо
известна с точностью до значения
параметра![]() .
Рассмотрим случайную величину
.
Рассмотрим случайную величину![]() ,
согласно рассмотренному выше свойству
функции распределения, случайная
величина
,
согласно рассмотренному выше свойству
функции распределения, случайная
величина![]() имеет равномерное распределение
имеет равномерное распределение![]() ,
не зависящее от параметра. Если при
фиксированных
,
не зависящее от параметра. Если при
фиксированных![]() ,…,
,…,![]() функция
функция![]() как функция параметра
как функция параметра![]() является непрерывной и монотонной,
тогда
является непрерывной и монотонной,
тогда![]() по определению является центральной
статистикой.
по определению является центральной
статистикой.
Для построения доверительного интервала
достаточно вычислить число
![]() ,
где
,
где![]() – уровень доверия,
– уровень доверия,![]() ,
тогда:
,
тогда:
![]() ,
,
где
![]() – функция распределения
– функция распределения![]() .
Поскольку
.
Поскольку![]() имеет равномерное распределение
имеет равномерное распределение![]() ,
то
,
то![]() и
и![]() ,
тогда:
,
тогда:
![]() ,
,
![]() .
.
Разрешая неравенства
![]() относительно
относительно![]() ,
получим доверительный интервал. Если
функция
,
получим доверительный интервал. Если
функция![]() возрастает по
возрастает по![]() ,
тогда:
,
тогда:
![]() .
.
Если функция
![]() убывает по
убывает по![]() ,
тогда:
,
тогда:
![]() .
.
Если функция
![]() возрастает по
возрастает по![]() ,
то для построения нижней доверительной
границы достаточно взять
,
то для построения нижней доверительной
границы достаточно взять![]() и рассмотреть вероятность:
и рассмотреть вероятность:
![]() ,
,
![]() ,
,
![]() .
.
Для построения верхней доверительной
границы достаточно взять
![]() и рассмотреть вероятность:
и рассмотреть вероятность:
![]() ,
,
![]() ,
,
![]() .
.
Если функция
![]() убывает по
убывает по![]() ,
то для построения нижней доверительной
границы следует взять
,
то для построения нижней доверительной
границы следует взять![]() и рассмотреть вероятность:
и рассмотреть вероятность:
![]() ,
,
![]() ,
,
![]() .
.
Для построения верхней доверительной
границы следует взять
![]() и рассмотреть вероятность:
и рассмотреть вероятность:
![]() ,
,
![]() ,
,
![]() .
.
7. Построение доверительных интервалов на основе асимптотической нормальности. Доверительный интервал для вероятности события.
Пусть
![]() – наблюдение и случайная величина
– наблюдение и случайная величина![]() имеет асимптотически (при
имеет асимптотически (при![]() )
нормальное распределение
)
нормальное распределение![]() :
:
![]() ,
при
,
при![]() ;
;
В силу асимптотической нормальности:
![]() ,
при
,
при![]() ,
,
тогда при больших
![]() справедливо приближенное равенство
для вероятностей:
справедливо приближенное равенство
для вероятностей:
![]() .
.
Пусть
![]() является квантилью распределения
является квантилью распределения![]() уровня
уровня![]() ,
где
,
где![]() – уровень доверия:
– уровень доверия:
![]() ,
,
тогда,
![]() .
.
Разрешая неравенство относительно
![]() ,
получим «приближенный» доверительный
интервал:
,
получим «приближенный» доверительный
интервал:
![]() .
.
Воспользуемся вышеизложенным методом
для построения «приближенного»
доверительного интервала неизвестной
вероятности события в схеме
![]() независимых испытаний. Пусть
независимых испытаний. Пусть![]() – выборка, в которой каждая случайная
величина
– выборка, в которой каждая случайная
величина![]() является бинарной и принимает значение
1 с некоторой неизвестной вероятностью
является бинарной и принимает значение
1 с некоторой неизвестной вероятностью![]() и значение 0 с вероятностью
и значение 0 с вероятностью![]() :
:
![]() .
.
Требуется построить приближенный
доверительный интервал для вероятности
![]() .
Рассмотрим случайную величину
.
Рассмотрим случайную величину![]() :
:
![]() .
.
К случайным величинам
![]() применима центральная предельная
теорема, в соответствии с которой сумма
применима центральная предельная
теорема, в соответствии с которой сумма![]() имеет асимптотически (при
имеет асимптотически (при![]() )
нормальное распределение с параметрами
)
нормальное распределение с параметрами ,
где:
,
где:
 ,
,
 ,
,
тогда случайная величина:

имеет асимптотически (при
![]() )
нормальное распределение
)
нормальное распределение![]() :
:
![]() ,
при
,
при![]() .
.
Пусть
![]() – квантиль распределения
– квантиль распределения![]() уровня
уровня![]() ,
тогда при больших
,
тогда при больших![]() :
:
![]() ,
,
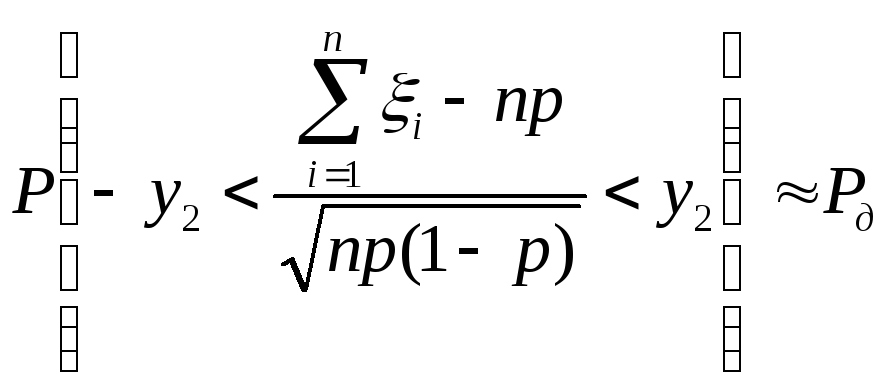 ,
,
 ,
,
 ,
,
 ,
,
где
![]() .
Разрешая неравенство относительно
неизвестной вероятности
.
Разрешая неравенство относительно
неизвестной вероятности![]() ,
получим:
,
получим:

![]()
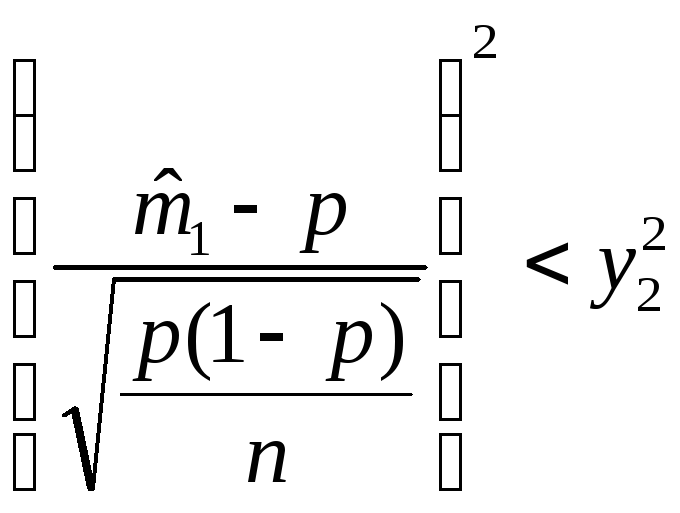
![]()

![]()

![]()

![]()

![]()

![]()

![]()

Пренебрегая слагаемыми с множителем
![]() и с множителем
и с множителем![]() под корнем, получим приближенное
неравенство:
под корнем, получим приближенное
неравенство:
 ,
,
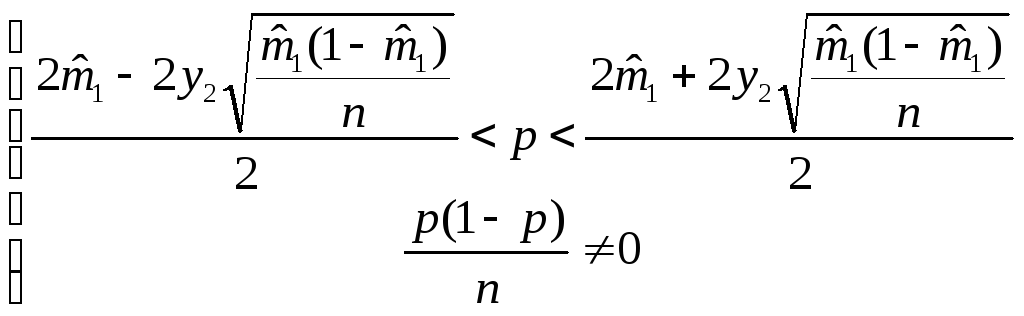 ,
,
 .
.
Таким образом,
 ,
,
и «приближенный» доверительный интервал
для вероятности
![]() имеет вид:
имеет вид:
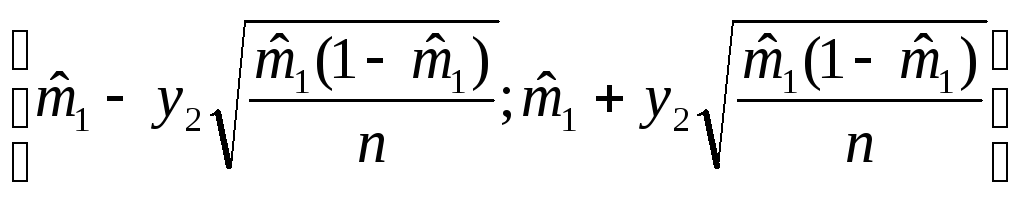 ,
,
где
![]() и
и![]() – квантиль распределения
– квантиль распределения![]() уровня
уровня![]() .
.

 ,
,