Тема 10. Методы статистических испытаний Монте-Карло.

1. Методы статистических испытаний.

Методы статистических испытаний – это совокупность методов численного решения прикладных задач с помощью моделирования случайных величин. Методы статистических испытаний находят применение во многих естественных науках (физики, химии, биологии, экономики), в многочисленных теориях (теория систем управления, теория систем массового обслуживания, теория надежности) и техники (радиотехники, аэродинамики).

Основная задача методов статистических испытаний заключается в вычислении исследуемой характеристики некоторого объекта (явления или процесса). В некоторых случаях получить точное значение исследуемой характеристики с позиций теоретического анализа объекта не представляется возможным, поскольку объект имеет очень сложную структуру или же структура объекта вовсе не известна. В таких случаях методами статистического моделирования проводится большое количество наблюдений над исследуемой характеристикой и полученный массив статистических данных обрабатывается таким образом, чтобы получить приближенное численное значение исследуемой характеристики. В большинстве таких случаев (например, когда объект не является естественным природным явлением, а является, к примеру, алгоритмом или системой) многократное испытание объекта для получения массива статистических данных производится с помощью моделирования случайных величин.

2. Методы получения случайных величин.

Для использования методов статистического моделирования требуется располагать реализацией вектора случайных величин , имеющего заданную функцию распределения (в общем случае каждая случайная величина является векторной). В частных случаях, все случайные величины имеют одинаковую функцию распределения , поэтому получение реализации сводится к -кратному получению реализации одной случайной величины с заданной функцией распределения .

Метод получения случайной величины с распределением .

Среди всех методов получения реализаций основными являются методы получения реализации случайной величины с равномерным распределением , часть из которых основана: а) на физических процессах, б) на функциях специального вида. Правильнее было бы сказать, что методы позволяют строить реализации случайной величины дискретного типа, которая с равной вероятностью принимает значения, равномерно рассредоточенные на отрезке , и потому функция распределения, которой оказывается близкой к функции распределения .

В некоторых методах, основанных на физических процессах, предварительно получают реализации случайной величины , принимающей с равной вероятностью значения 0 и 1:

(10.1)

Например, некоторый датчик регистрирует в течение фиксированного отрезка времени количество частиц распада от источника радиоактивного излучения, если количество частиц оказывается четное, то считается, что реализация случайной величины равна 0, если количество частиц нечетное, то считается, что реализация случайной величины равна 1. В качестве другого примера можно указать датчик, регистрирующий количество флуктуаций напряжения в радиоэлектронном элементе (дробовый эффект в лампах). Если количество флуктуаций четное, то реализация считается равной 0, если нечетное – 1.

Предположим, что получен вектор , в котором все величины независимы и каждая случайная величина является величиной вида (10.1), образуем новую случайную величину :

(10.2)

Легко видеть, что наименьшее значение равно 0 (все ), а наибольшее значение равно 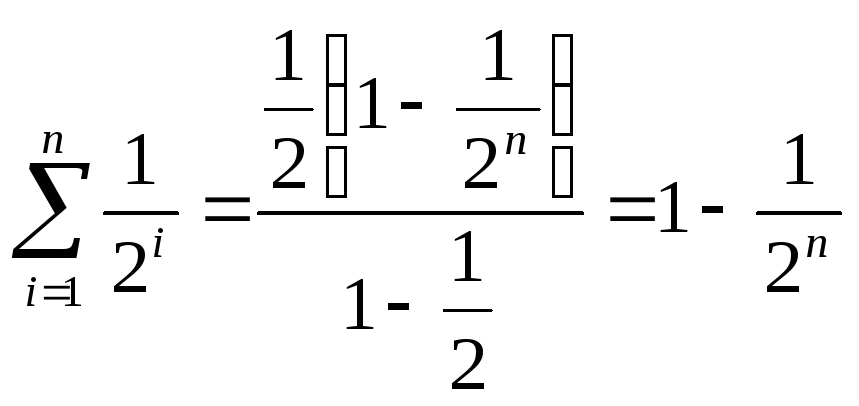(все ), причем все значения величины равномерно рассредоточены на отрезке с шагом и все значения величина принимает с равной вероятностью. Отсюда следует, что при больших функция распределения случайной величины незначительно отличается от функции распределения случайной величины , равномерно распределенной на отрезке .

В методах, основанных на функциях специального вида, используется рекуррентные вычисления: пусть , …, уже имеющиеся случайные величины, тогда остальные величины вычисляют рекуррентно:

,

,

где функция подбирается таким образом, чтобы величина имела функцию распределения близкую к функции распределения . Вопрос получения величин , …, , как правило, разрешается за счет привлечения другого метода.

Широкое распространение получили линейно конгруэнтные методы, в которых функция сочетает в себе линейную функцию и операцию приведения по модулю:

.

Для эффективной реализации число обычно полагают равным , в этом случае приведение по модулю сводится к отбрасыванию всех битов старше . В наиболее простом случае:

,

– произвольное.

Легко видеть, что различных значений в последовательности не больше (в силу приведения по модулю) и поскольку следующее значение зависит только от одного значения (непосредственно предшествующего), то, начиная с некоторого номера , последовательность значений начнет повторяться, отсюда число имеет название периода. Считается, что чем больше период , тем лучше метод, поэтому постоянные и стараются выбирать так, чтобы оказалось наибольшим (наибольшее значение равно ). В качестве конкретных примеров можно указать следующие методы:

, – произвольное.

, – произвольное.

Метод получения бинарных случайных величин.

Предположим, каким-то образом составлен метод получения величин , имеющих равномерное распределение , и требуется составить метод получения бинарных величин , которые с вероятностью принимают значение 1 и с вероятностью – значение 0:

(10.3)

Легко видеть, что таким методом является, например, метод полагающий:

,

поскольку,

,

.

С помощь величин моделируется наступление события , имеющего заданную вероятность : если , то событие в испытании с номером не наступило, если , то событие в испытании с номер наступило.

Заметим, что в действительности имеются не величины с равномерным распределением , а некоторые другие величины , имеющие распределение близкое к равномерному распределению , поэтому вместо получаются случайные величины :

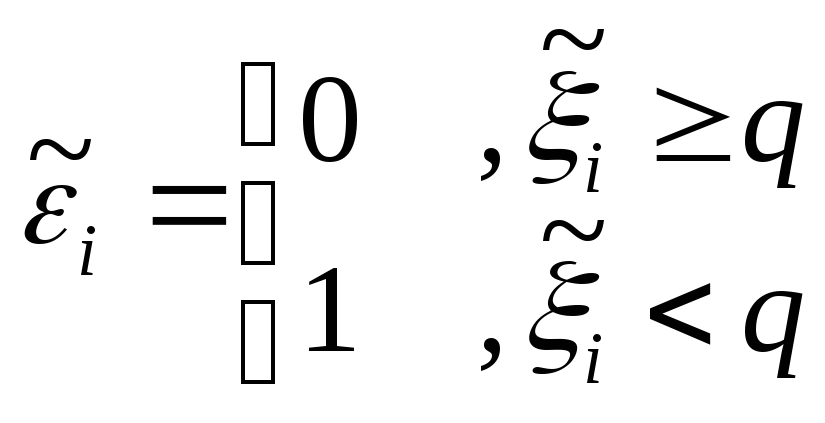
В частности, величины , полученные по методу (10.2), принимают лишь значения вида , где , отсюда следует:

,

.

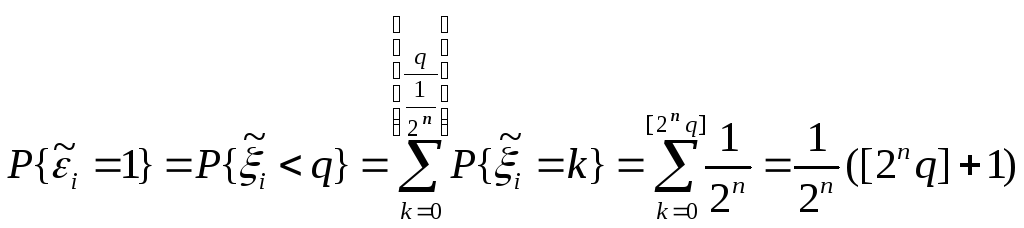Таким образом, с помощью величин могут быть получены лишь такие случайные величины , для которых при некотором , в этом случае в качестве следует брать значение , тогда распределения и совпадают:

.

Поскольку , то

,

то есть с помощью величин можно получить только случайные величины с вероятностью , отсюда следует, что события и величины вероятностью не могут быть представлены величинами , получаемыми с помощью .

Метод получения случайных величин с распределением .

Предположим, имеется способ получения бинарных величин вида (10.3), тогда, получив таких случайных величин, легко образовать случайную величину , имеющую биномиальное распределение :

.

Метод получения случайных величин с распределением .

Методы получения случайных величин с нормальным распределением, основаны на центральной предельной теореме: пусть , …, – случайные величины с равномерным распределением , полученные одним из методов представленных выше, тогда случайная величина :

,

имеет при больших распределение близкое к стандартному нормальному распределению . Поскольку нормальное распределение сохраняется при линейных преобразованиях, то с помощью случайной величины можно получить случайную величину , имеющую при больших распределение близкое к нормальному :

.

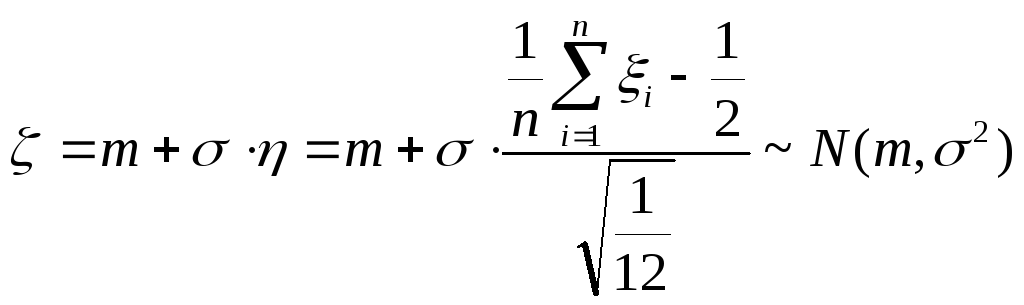Метод получения векторных случайных величин с распределением .

Пусть методом, представленным выше, получены случайные величины , …, , которые имеют распределение и некоррелированы (или коэффициенты корреляции настолько малы, что ими можно пренебречь). Будем считать, что вектор имеет нормальное распределение , где – нулевой вектор порядка и – единичная матрица порядка . Образуем вектор с помощью линейного преобразования вектора :

,

где – некоторая матрица порядка . Вектор имеет нормальное распределение, поскольку получен с помощью линейного преобразования вектора , имеющего нормальное распределение. Математическое ожидание :

.

Остается лишь выбрать матрицу таким образом, чтобы дисперсионная матрица вектора оказалась равной заданной матрице . По свойству дисперсионной матрицы:

,

откуда следует, что матрица должна удовлетворять равенству:

.

Ковариационная матрица всегда симметрична и в некоторых случаях положительно определена, для таких матриц существует матрица , удовлетворяющая , причем матрицу можно сделать нижнетреугольной (для эффективной организации вычислений).

В частности для получения вектора с распределением , где – коэффициент корреляции, , , достаточно выполнить следующее преобразование:

.

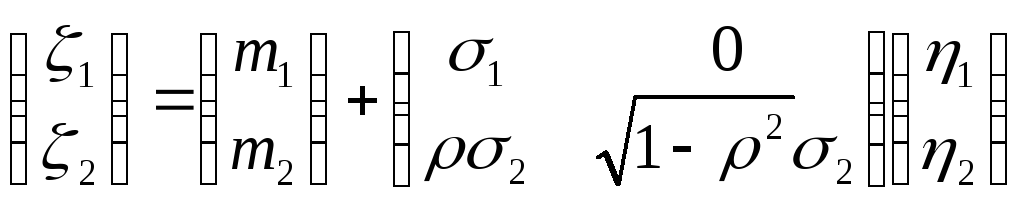Метод получения случайной величины с заданной функцией распределения.

Пусть – случайная величина, имеющая равномерное распределение (или распределение «близкое» к ), полученная одним из методов, представленных выше.

Если требуется получить случайную величину непрерывного типа с функцией распределения , имеющей обратную функцию , тогда образуем случайную величину :

.

Легко видеть, что функция распределения есть функция действительно:

,

, , – функция распределения величины .

Если требуется получить случайную величину дискретного типа, принимающую конечное число значений , , …, с вероятностями , , …, , тогда образуем случайную величину :

.

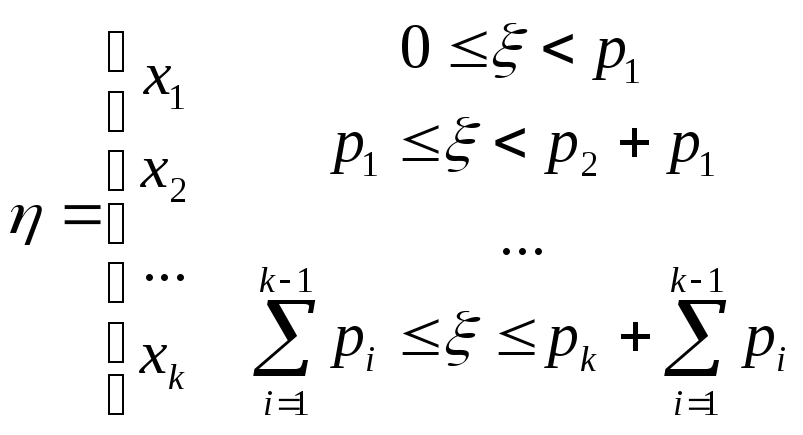Легко видеть, что случайная величина принимает значение с вероятностью :

,

.

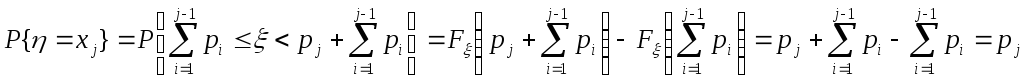Строго говоря, получить случайную величину дискретного типа, принимающую счетное число значений , , … с вероятностями , …, не представляется возможным. Тем не менее, поскольку ряд составленный из вероятностей сходится, то остаток ряда стремиться к нулю, отсюда следует, что можно выбрать число такое, что , где малое число (например, ). Случайная величина принимает значения , , … с малой вероятностью (меньше чем ), поэтому этими значениями на практике можно пренебречь и приписать оставшуюся вероятность к вероятности значения . В этом случае, воспользовавшись методом, представленным выше, можно получить случайную величину, принимающую конечное число значений , …, , с вероятностями , …, , .

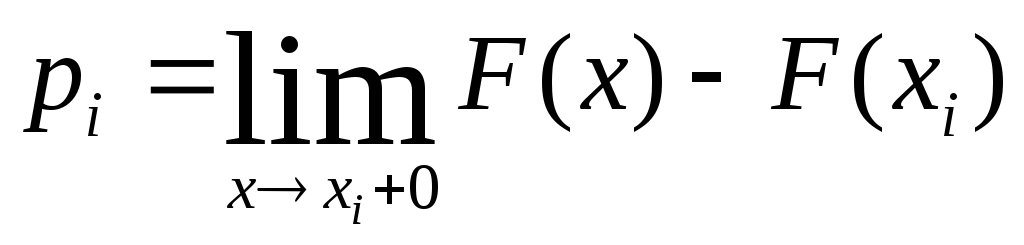Если требуется получить случайную величину смешанного типа, то необходимо комбинировать представленные выше методы: если для полученного значения определена обратная функция , то следует положить , если же для полученного значения обратная функция не определена (в силу разрыва в некоторой точке величины ), то следует положить .