Тема 2. Точечное оценивание вероятностей и моментов. Линейная оценка среднего с наименьшей дисперсией.

1. Состоятельность оценок.

Состоятельность является важным свойством оценок, но установление свойства состоятельности непосредственно из определения (доказательство сходимости по вероятности) в некоторых случаях оказывается затруднительным, поэтому часто прибегают к использованию предельных теорем (теорема Бернулли, теорема Гливенко, теорема Хинчина, теорема Чебышева), «арифметических» свойств сходимости по вероятности и вспомогательных утверждений.

Теорема(Бернулли)

Пусть – количество появлений событиявнезависимых испытаниях, тогда последовательность относительных частотсходится по вероятности к вероятности события, при:

, при.

Теорема(Хинчин)

Пусть ,, … – последовательность взаимно независимых случайных величин, имеющих одинаковую функцию распределения с конечным математическим ожиданием, тогда последовательность случайных величинсходится по вероятности к, при:

, при.

Утверждение(неравенство Чебышева)

Пусть случайная величина имеет конечную дисперсию,, тогда:

.

Теорема(закон больших чисел в форме Чебышева)

Пусть ,, … – последовательность взаимно независимых случайных величин, имеющих конечные математические ожидания,, … и конечные дисперсии,, … соответственно.

Если,

,

Тогда последовательность арифметических средних случайных величин сходится по вероятности к арифметическому среднему математических ожиданийпри :

, при.

Утверждение 2.1.

Пусть – наблюдения, и статистикаявляется несмещенной оценкой величины, причем дисперсииконечны и стремятся к нулю с ростом:

,

,

,

тогда является состоятельной оценкой.

Доказательство:

При любом в силудля статистикисправедливо неравенство Чебышева:

,

откуда,

.

Для произвольных ивсегда можно выбратьтакое, чтои посколькуи, то длявсегда можно найтитакое, что для всех,, тогда:

,

что в точности по определению означает сходимость по вероятности статистики кпри:

, при.

По условию статистика является несмещенной оценкой, то есть, тогдасходится по вероятности к:

, при,

что по определению означает, что является состоятельной.

Утверждение доказано.

2. Точечное оценивание вероятности события.

Пусть проводится независимых испытаний, в каждом из которых может произойти некоторое событие, имеющее вероятность, которая не известна. Требуется построить оценку неизвестной вероятности.

Пусть – выборка, в которой каждая случайная величинапринимает значение равное единице, если в-ом испытании произошло событие, и значение равное нулю, если в-ом испытании событиене произошло:

Случайная величина количества появлений событиявиспытаниях равна сумме:

.

Возьмем в качестве оценки неизвестной вероятности случайную величину относительной частоты:

.

Легко видеть, что является несмещенной оценкой, действительно:

.

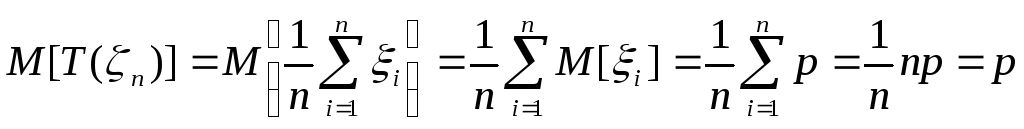Согласно теореме Бернулли имеет место сходимость по вероятности случайной величины к вероятности, отсюда следует, что оценкаявляется состоятельной.

3. Точечное оценивание значений функции распределения.

Пусть выборка из распределенияс неизвестным параметром, инекоторое фиксированное числовое значение, требуется построить оценку значения функции распределения – неизвестной величины(неизвестной в силу того, что параметрнеизвестен) и исследовать свойства несмещенности и состоятельности построенной оценки.

Предположим, что в качестве оценки неизвестной величины вероятностииспользуется значение эмпирической функции распределения,

,

где согласно определению эмпирической функции распределения 1.6функцияравна случайной величине количества случайных величин выборкименьших. Заметим, что функциюможно представить в виде суммы значений индикаторных функций от случайных величин выборки:

,

где () принимает значение 1 еслии 0 в противном случае. Таким образом, каждая величинаявляется случайной величиной, принимающей лишь два значения: 1 с вероятностьюи 0 с вероятностью:

.

Поскольку выборка из распределения, то в соответствии с определением выборки1.1, все случайные величины имеют функцию распределения, отсюда следует, что,

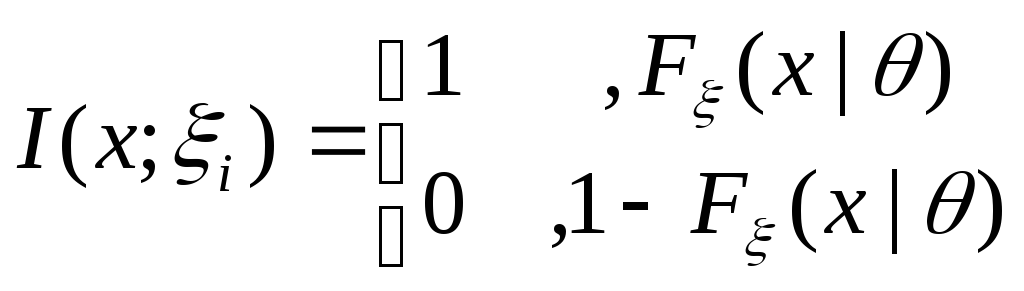
Таким образом, окончательно статистика имеет вид:

(2.1)

где - случайные величины,

.

Исследуем свойства оценки (2.1), покажем, что статистика (2.1) является несмещенной оценкой , действительно, по свойству математического ожидания,

.

Для исследования свойства состоятельности оценки достаточно вспомнить теорему о сходимости по вероятности значений эмпирической функции распределенияк значениямпри всяком фиксированном. Поскольку оценкав точности совпадает с, то очевидносходится по вероятности кприи, следовательно, является состоятельной.