3. Доверительный интервал для дисперсии нормального распределения с известным математическим ожиданием.

Пусть – выборка из нормального распределения с известным математическим ожиданиеми неизвестной дисперсией, построим доверительный интервал для дисперсиис уровнем доверия.

Рассмотрим статистику :

.

Поскольку случайные величины имеют нормальное распределениеи независимы, то статистикаимеет распределение(«хи-квадрат сстепенями свободы») и кроме того одновременно при всех реализациях выборкифункциякак функция параметра:

является непрерывной и убывающей. Таким образом, статистика является центральной статистикой для.

Для построения доверительного интервала выберем числа итак, чтобы выполнялось равенство:

.

Для выполнения равенства достаточно, например, в качестве взять квантиль уровняраспределения, а качестве– квантиль уровняраспределения, действительно:

,

где – случайная величина, имеющая распределение, и– функция распределения.

При таких значениях иполучается так называемый «центральный интервал» (название обусловлено тем, что слева от«сосредоточена» вероятностьи справа от«сосредоточена» вероятность). Построение «наикратчайшего» доверительного интервала, то есть нахождение чиселис наименьшей разностьюсреди всех чисел удовлетворяющих, в данном случае является технически сложным ([1] стр. 86), поэтому на практике ограничиваются более простым «центральным интервалом».

Преобразование неравенств приводит к следующему доверительному интевалу:

,

,

.

Поскольку последнее равенство справедливо при всяком значении , то интервал:

,

где и– квантили уровнейираспределениясоответственно, является доверительным интервалом дляс уровнем доверия.

Нетрудно также получить и доверительный интервал для с.к.о. , действительно, поскольку:

,

то

,

тогда при тех же значениях иинтервал:

является доверительным интервалом для с уровнем доверия.

4. Доверительный интервал для дисперсии нормального распределения с неизвестным математическим ожиданием.

Теорема 5.5.(Фишер)

Пусть – выборка из нормального распределения, статистикии, тогда:

1) Статистика имеет распределение;

2) Статистики и– независимые случайные величины.

Доказательство:

1) Преобразуем статистику следующим образом:

.

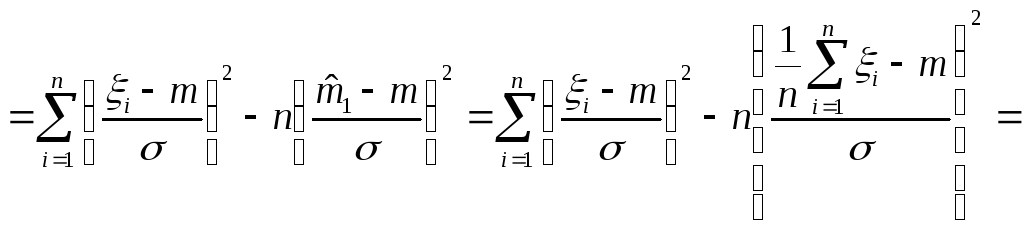
Определим вектор-столбец случайных величин :

,

тогда,

.

Поскольку случайные величины имеют нормальное распределение, то случайные величинытакже имеют нормальное распределение (как линейное преобразование нормальной случайной величины). Легко видеть, что математическое ожиданиеесть нулевой вектор:

,

и дисперсионная матрица является единичной матрицей, поскольку:

,

где припосколькуинезависимы (- выборка по условию теоремы).

Пусть – ортогональная матрица (т.е., где– транспонированная матрица), в которой все элементы первой строки равны:

(5.1)

Определим вектор-столбец случайных величин :

,

.

Каждая случайная величина имеет нормальное распределение, поскольку всеимеют нормальное распределение. Математическое ожиданиеесть нулевой вектор:

,

и дисперсионная матрица есть единичная матрица, поскольку:

,

поскольку – ортогональная матрица (). Таким образом, случайные величинынекоррелированные и поскольку всеимеют нормальное распределение, то следовательно случайные величинынезависимы.

Покажем, что , действительно:

.

Из определения матрицы (5.1):

(5.2)

Таким образом,

(5.3)

где все величины имеют нормальное распределение и независимы, поэтому статистикаимеет распределение.

2) Из (5.2) следует:

Из (5.3) следует:

.

Поскольку случайные величины независимы, то следовательно независимыи.

Теорема доказана.

Теорема 5.5позволяет построить доверительный интервал для дисперсии нормального распределение в случае, когда математическое ожидание неизвестно. Пусть– выборка из нормального распределения, из теоремы5.5следует, что статистика:

имеет распределение , не зависящее от неизвестных параметрови, и одновременно при всех реализациях выборкифункциякак функцияявляется непрерывной и убывающей. Следовательно, статистикаявляется центральной статистикой для. Пустьи– квантили уровнейираспределения, тогда:

,

,

.

Таким образом, интервал

,

где иявляются квантилями уровнейираспределения, является доверительным интервалом для дисперсиис уровнем доверия. Заметим, что при тех же значенияхиинтервал

является доверительным интервалом для с.к.о. с уровнем доверия.