15.Свойства критерия хи-квадрат(состоятельность, мощность критерия, нецентральное распределение хи-квадрат). Применение Критерия для проверки гипотезы о распределении.

Состоятельность:

β(P)=P(откл. H/: p ≠)1 - мощность критерия.

Теорема: если H не верна, т.е. p ≠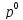, то прираспределениестремится к нецентральному распределению(a), а – параметр нецентральности

Нецентральное распределение 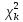(a):

=,

=

M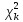(a)=k+a

D

Проверка гипотезы о распределении:

Выборка -

Проверяется гипотеза H:

Разобьём диапазон значений с.в. на m промежутков

попадания в i-й промежуток

Одно из набл. Может закончится попаданием:

P(=H:

16.Критерий хи-квадрат в случае неизвестных параметров. Проверка гипотезы о независимости признаков.

Критерий хи-квадрат в случае неизвестных параметров:

Выборка -

Проверяется гипотеза H:

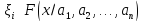
Разобьём диапазон значений с.в. на m промежутков

попадания в i-й промежуток

Одно из набл. Может закончится попаданием:

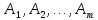
P(=(H:

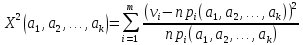
Пусть - оценка поmin

: >h, то H отклоняется

h: P(ош./H) = α

P(>h/H) = α

Теорема Фишера: если H верна и n, распределение статистики сходится к

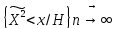PP

Проверка гипотезы о независимости признаков:

Предположим, имеется большая совокупность объектов, каждый из которых обладает двумя признаками А и В; признак А имеет m уровней: A₁, ..., A_m, а признак В – k уровней: B₁, ..., B_k . Пусть уровень А_i встречается с вероятностью P(A_i), а уровень B_j - c вероятностью P(B_j). Признаки А и В независимы, если

P(A_i B_j) = P(A_i)P(B_j), i = 1, ..., m, j = 1, ..., k ,

т.е. вероятность встретить комбинацию A_i B_j равна произведению вероятностей. Пусть признаки определены на n объектах, случайно извлеченных из совокупности; _ij - число объектов, имеющих комбинацию A_i B_j, =n. требуется проверить гипотезу Н о независимости признаков А и В. Задача сводится к случаю с неизвестными параметрами; ими являются вероятности

P(A_i), i = 1, ..., m; P(B_j), j = 1, ..., k,

всего (m-1) + (k-1); их оценки:

,

. (10)

Если гипотеза Н верна, то по теореме Фишера асимптотически распределена по закону хи-квадрат с числом степеней свободы

f = mk - 1 - (m - 1) - (k - 1) = (m - 1)(k - 1),

и потому, если

, (11)

то гипотезу о независимости признаков следует отклонить.

Ясно, что по (10) - (11) можно проверять независимость двух случайных величин, разбив диапазоны их значений на m и k частей.

17. Проверка гипотезы об однородности выборок

 1-я выборка: -n₁ наблюдений

2-я выборка: –n₂ наблюдений

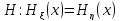
Разбиваем допустимую область на m частей:

Попадание в промежуток:

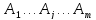
1 выб. ;

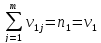
2 выб. ;H:

Составляем (*)

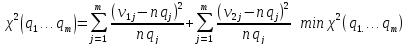­– это выражение подставляем в (* ) ()

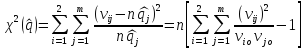
Если H верно, то

Обобщение для k выборок:

Если H верно, то

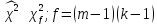
18. Критерий согласия Колмогорова

Проверяется гипотеза H о том, что последовательность независимых наблюдений извлечена из совокупности с непрерывной ф-ей распределения . Строим вариационный ряди ф-ю эмпирического распределения. Мерой качества согласования эмпирического и гипотетического распределения примем максимальное отклонение функции эмпирического распределениягипотетического, то есть максимум модуля разности

. Распределение статистики при истинностиH не зависит от

Если тоH отклоняется.

–табл. (статистические таблицы Большева, Смирнова)

;

Ассимптотическое распределение для

;

если ;

если