
- •41.Наибольшее и наименьшее значение функции на отрезке.
- •42.Выпуклость функции. Точки перегиба.
- •44. Общая схема исследования функций и построения их графиков.
- •Определение, предел и непрерывность функции нескольких переменных.
- •Частные производные первого и высших порядков.
- •48.Определение экстремума функции двух переменных. Необходимые и достаточные условия экстремума функции двух переменных.
- •Первообразная функции и неопределенный интеграл.
- •54.Таблица основных интегралов
- •55. Интегрирование при помощи подстановки.
- •56.Интегрирование по частям.
- •Интегрирование рациональных функций. Метод неопределенных коэффициентов.
41.Наибольшее и наименьшее значение функции на отрезке.
Т. Если ф-ция определена и непрерывна на отрезке, то она достигает на нем своего наименьшего и наибольшего значения
Т. Если непрерывная ф-ция имеет на отрезке единственный локальный экстремум, то он будет являться наибольшим значением в случае максимума, и наименьшим в случае минимума.
Алгоритм исследования
1.Найти значения на концах отрезка. 2. Найти внутренние точки отрезка, где производная равна нулю или не существует, и вычислить значения в этих точках. 3. Из вычисленных значений выбрать наибольшее и наименьшее значения функции.
Т.Если функция непрерывна на отрезке [a;b], и на интервале (a;b) производная меньше нуля (больше нуля), то наибольшее значение будет на левом конце, а наименьшее – на правом (наименьшее - на левом; наибольшее – на правом)
42.Выпуклость функции. Точки перегиба.
График дифференцируемой функции в интервале (а,b) функции - называют выпуклым (вогнутым), если он расположен ниже (выше) любой совей касательной.

Т.
«Достаточный признак выпуклости
(вогнутости) графика функции» Если
функция
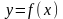 во
всех точках интервала
во
всех точках интервала
 имеет
вторую производную меньше (больше) нуля,
то во всех точках интервала кривая
выпукла (вогнута)
имеет
вторую производную меньше (больше) нуля,
то во всех точках интервала кривая
выпукла (вогнута)
(При доказательстве теоремы используют уравнения касательной к графику функции в точке и теорему Лагранжа)
Точка графика непрерывной функции, в которой выпуклость изменяется на вогнутость или наоборот называют точкой перегиба.
Т.
«Достаточный признак существования
точки перегиба»: Если в точке
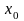 функция
f(x)
имеет первую производную, вторая
производная в точке
равна
нулю или не существует, и кроме того,
при переходе через точку x0
вторая производная меняет знак,
функция
f(x)
имеет первую производную, вторая
производная в точке
равна
нулю или не существует, и кроме того,
при переходе через точку x0
вторая производная меняет знак,
то точка с координатами (x0, f(x0))является точкой перегиба графика функции y=f(x)
.Д-во Так как функция дифференцируема в точке, то она непрерывна в этой точке и существует значение функции f( ).
Рассмотрим
случай
 при
при
 и
и
 при
при
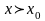 .
Согласно достаточному признаку выпуклости
(вогнутости) получаем, что слева от точки
кривая выпуклая, а справа – вогнутая.
Следовательно, точка координатами есть
точка перегиба графика функции с
выпуклости на вогнутость. (Аналогично
доказывается случай
при
и
при
)
.
Согласно достаточному признаку выпуклости
(вогнутости) получаем, что слева от точки
кривая выпуклая, а справа – вогнутая.
Следовательно, точка координатами есть
точка перегиба графика функции с
выпуклости на вогнутость. (Аналогично
доказывается случай
при
и
при
)
43. Асимптоты графика функции.
Прямая
х=а
называется вертикальной
асимптотой
к графику функции
,
если хотя бы один из пределов f(а+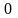 )
или
f(a+
)
равен
)
или
f(a+
)
равен
 (
(
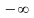 )
)
Прямая
y=kx+b
называют
невертикальной
(наклонной)
асимптотой
к графику функции
при
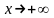 (
( ),
если f
(х)= k
),
если f
(х)= k x+b+a(x),
где a(x)-бесконечно
малая функция при
(
)
x+b+a(x),
где a(x)-бесконечно
малая функция при
(
)
Т.
Для того, чтобы прямая у=k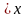 +b
являлась
невертикальной асимптотой графика
функции y=f(x)
при
(
)
необходимо и достаточно существования
двух пределов:
+b
являлась
невертикальной асимптотой графика
функции y=f(x)
при
(
)
необходимо и достаточно существования
двух пределов:
предела
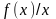 при
(
),
который равен угловому коэффициенту
k
невертикальной асимптоты и предела
при
(
),
который равен угловому коэффициенту
k
невертикальной асимптоты и предела
 при
(
),
который
равен начальной ординате b
невертикальной асимптоты.
при
(
),
который
равен начальной ординате b
невертикальной асимптоты.
Вертикальных асимптот может быть сколько угодно, а невертикальных не может быть более двух
44. Общая схема исследования функций и построения их графиков.
1) Найти область определения.
Найти область значений (если это возможно, а если невозможно, то сделать это в конце исследования).
Исследовать на четность и периодичность.
Исследовать на непрерывность.
Найти асимптоты.
Найти промежутки возрастания, убывания и экстремумы.
Исследования на выпуклость и вогнутость, точки перегиба
8)Найти точки пересечения с координатными осями. 9. Построить график
