№2.Основные понятия теории игр. Матричные игры

Лабораторная работа № 2

Тема: Основные понятия теории игр. Матричные игры

Цель работы: 1.Ознакомиться с разделом исследования операций - теорией игр.

2.Научиться моделировать задачи и находить их решение в чистых стратегиях.

Раздел исследования операций, связанный с математическим моделированием условий конфликта и поиском на этой основе оптимальных решений называют теорией игр.

Основные понятия теории игр

Под термином “игра” понимается “математическая модель конфликта”. Обозначим U - множество конфликтующих сторон. Произвольно взятая сторона AU располагает некоторым набором (множеством) S_A допустимых (определённых правилами игры) стратегий S_1A,S_2A,..., т.е. S_A={S_1A,S_2A,...}. Стратегией называется совокупность правил, определяющих выбор варианта действий в зависимости от сложившейся ситуации. Формально, стратегия -функция x=(y,z), отображающая NZM, где N - неопределенные, Z - случайные, M - контролируемые факторы.

Использование каждой стороной какой либо из своих стратегий определяет один из возможных исходов конфликта, принадлежащий множеству J всех возможных исходов. Реализацией игры называется отображение S_A1S_A2S_A3... J. На множестве J задаётся числовая функция C_A(j), jJ, называемая платёжной функцией. Она определяет размеры выигрыша (положительного или отрицательного), получаемого стороной A при исходе j. Таким образом, давая формальное определение игры, можно сказать, что игра-это система J, объединяющая компоненты U, {S_A}_AU, J, {C_A(j)}_{AU, jJ}.

Классификация игр по различным признакам

1. Если у каждого участника игры имеется конечное число стратегий, то игра называется конечной. Если хотя бы один участник имеет в своём распоряжении бесконечно много стратегий, то игра называется бесконечной.

2. Игры, где возможно объединение участников для совместных действий (образование коалиций), называются кооперативными. Если в игре образование коалиций невозможно, то такая игра называется бескоалиционной.

3. Противником оперирующей стороны может быть:

a) разумный противник, который стремится так выбрать свою стратегию, чтобы получить для себя наибольшую выгоду.

b) “природа” - нейтральный противник (в понятие “природа” вкладывается вся совокупность внешних обстоятельств, в которых приходится принимать решение). Природу нельзя рассматривать как разумного противника, который мог бы использовать ошибки, совершаемые человеком.

Антагонистические игры

Рассмотрим конечную бескоалиционную игру G, в которой участвуют два игрока A и B.

Пусть A₁ ... A_m - стратегии игрока A,

B₁ ... B_n - стратегии игрока B,

C_A(i,j) - выигрыш игрока A, если он применяет стратегию A_i, а B применяет стратегию B_j

C_B(i,j) - выигрыш игрока B, таком же случае.

Если C_A(i,j) + C_B(i,j) = 0 для i, j, то игра называется игрой с нулевой суммой или антагонистической. В таких играх выигрыш одного игрока определяется проигрышем другого (C_A(i,j)= - C_B(i,j)), поэтому её можно задать матрицей C(i,j) с элементами {a_ij}, являющимися выигрышами для игрока А (проигрышами игрока В), строки которой соответствуют стратегиям A, а столбцы - стратегиям B. Эту матрицу называют платёжной.

Ai\Bj	B1	B2	...	Bn
A1	a11	a12	...	a1n
A2	a21	a22	...	a2n
...	...	...	...	...
Am	am1	am2	...	amn

Сторона A пытается найти наилучшую из своих стратегий, оценивая выигрыши a_ij поочерёдно для A₁,A₂, ... A_m. Очевидно, при использовании стратегии A_i безусловно достижимым (гарантированным) будет 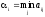. Тогда наилучшей с точки зрения A оказывается та стратегия, для которой _i максимально и - наилучший гарантированный результат для игрока A. Если A будет придерживаться этой стратегии, то выиграет не меньше при любом поведении B. В силу этого величина называется нижней ценой игры.

Аналогично для игрока B. В этом случае речь идёт о проигрышах стороны A, так как в антагонистической игре C_B(i,j)= - C_A(i,j)= - a_ij. Следовательно, произвольно взятая стратегия B_j (1jn) должна характеризоваться показателем , определяющим наибольший из ожидаемых проигрышей. Тогда наилучшей для B становится стратегия, дающая минимум _j, равный 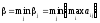она называется минимаксной стратегией. Величина называется верхней ценой игры. Если второй игрок будет применять оптимальную стратегию, то больше чем он не проиграет. Легко показать, что .

Рассмотрим два случая:

1. = ;

2. < .

1)Равенство = означает, что в платёжной матрице присутствует элемент a_ij, который одновременно оказывается минимальным в i-й строке и максимальным в j-м столбце (1im, 1jn, a_ij==). В этом случае элемент a_ij называется седловой точкой.

Примером может служить матрица:

Ai\Bj	B1	B2	B3	B4	i
A1	2	4	7	5	2
A2	7	6	8	7	6
A3	5	3	4	1	1
j	7	6	8	7

В игре с седловой точкой стороны A и B, решившие придерживаться минимаксных стратегий, попадают в ситуацию, когда и для A, и для B невыгодно изменять стратегии. Если в какой-то момент один из участников попытается изменить свою стратегию, то выгоду из этого извлечёт другой участник. Положение, при котором ни одна из сторон не имеет никаких разумных оснований для изменения своей стратегии, называется ситуацией равновесия. В играх с седловой точкой такая ситуация возникает если стороны A и B используют A_i и B_j. Величина a_ij== называется ценой игры, стратегии A_i и B_j - оптимальными.

2)В случае < в матрице не существует седловой точки и не возникает ситуации равновесия, поэтому игроки вынуждены менять свои стратегии. В этом случае для определения решения игры вводится понятие смешанной стратегии. Смешанной стратегией игрока A называется полный набор вероятностей применения стратегий A₁ ... A_m, т.е. вектор P т.ч. P=(p₁,p₂,...p_m), p_i0, , где p_i - вероятность выбора i-й стратегии (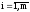). Стратегии A₁ ... A_m при этом называются чистыми. Стратегии A_k , для которых p_k>0, называются активными. Аналогично для игрока B, смешанной стратегией называется вектор Q т.ч. Q=(q₁,q₂,...q_n), q_j0, , где q_j - вероятность выбора j-й стратегии (). Оценка эффективности смешанных стратегий производится с точки зрения среднего выигрыша, который представляет собой математическое ожидание выигрыша игрока А (проигрыша игрока В):

.

Наилучший гарантированный результат для игрока A - , для игрока B - 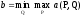. Стратегии, при которых достигаются a и b называются оптимальными смешанными стратегиями. Теорема о минимаксе утверждает, что величины a и b связаны между собой: в конечной игре двух лиц с нулевой суммой и полной информацией имеет место равенство a = b. Величина =a=b называется ценой игры. При этом существует пара оптимальных стратегий P^* и Q^*, таких что a(P^*,Q^*)=.

Имеет место основная теорема теории игр: если один из игроков придерживается оптимальной смешанной стратегии, то средний ожидаемый выигрыш равен , независимо от действий противника в рамках его активных стратегий. Таким образом, любая конечная игра двух лиц с нулевой суммой имеет по крайней мере одно решение либо в чистых, либо в смешанных стратегиях.

Пример 1. Игра “Три пальца”.

Два игрока выкидывают одновременно и независимо друг от друга один, два или три пальца. Выигрыш - число выкинутых пальцев. Если сумма - числа чётное, то платит A, а если нечётное, то платит B.

Решение: Составляем платёжную матрицу

A₁, B₁ : 1 + 1 = 2 - чётное, поэтому A получает 2

A₁, B₂ : 1 + 2 = 3 - нечётное, поэтому A платит 3 и т. д.

A\B		B1		B2		B3	i
A1		2		-3		4	-3
A2		-3		4		-5	-5
A3		4		-5		6	-5
j	4		4		6

Находим _i - минимальные числа в строках, _j - максимальные числа в столбцах. Из них выбираем

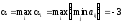, и .

Получаем: -3 < 4 ( < ), т.е. игра не имеет седловой точки и не имеет решения в чистых стратегиях.

Пример 2. Противовоздушная оборона.

У игрока A имеется три типа вооружений A₁, A₂, A₃ (зенитки, ракеты, самолёты), а у игрока В самолёты трёх типов. А - обороняется, В - нападает. Цель игрока А перехватить и сбить самолет противника, а цель В - сохранить свой самолёт. Если А применяет зенитки A₁, то поражает самолёты В с вероятностями 0.5, 0.6, 0.8; игрок В при этом старается применить самолёт, для которого вероятность поражения наименьшая. Если А применяет ракеты A₂, то поражает самолёты В с вероятностями 0.9, 0.7, 0.8. Когда А пускает в ход самолёты - истребители A₃, то поражает самолёты В с вероятностями 0.7, 0.5, 0.6. Определить оптимальную стратегию для игрока А.

Решение: Строим платежную матрицу:

A\B	B1	B2	B3	i
A1	0.5	0.6	0.8	0.5
A2	0.9	0.7	0.8	0.7
A3	0.7	0.5	0.6	0.5
j	0.9	0.7	0.8

Находим нижнюю и верхнюю цену игры

,

.

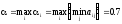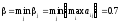Игра имеет седловую точку (α₂;β₂). Оптимальными стратегиями для A и B будут соответственно A₂ и B₂.

Задание к лабораторной работе № 2

Построить математическую модель следующих задач в форме матричной игры. Пользуясь принципом минимакса найти решения этих задач или установить, что они не решаются в чистых стратегиях (задачи приводятся с двумя вариантами числовых данных).

1.Два противника А и В ведут борьбу за два стратегических пункта. Под командованием А находится два (три) полка, под командованием В - три (три). Обе стороны должны распределить свои силы между двумя пунктами. Пусть n₁ и n₂ числа полков, посланных со стороны А на пункты 1 и 2 соответственно. Аналогично, пусть m₁ и m₂ - распределения полков противника по соответствующим пунктам. Выигрыш А подсчитывается следующим образом: если n₁>m₁, то он получает m₁+1, и, если n₂>m₂, он получает m₂+1. С другой стороны, если n₁<m₁, то он теряет n₁+1, и, если n₂<m₂, он теряет n₂+1. Если число полков на каждой стороне одно и тоже, то каждая сторона получает нуль. Определить оптимальные стратегии для каждого игрока.

2.Два предприятия предполагают выпустить конкурирующие товары. Первое - А или В, второе - С или D, причем одновременный выпуск двух типов товаров каждым из предприятий признан экономически невыгодным. По прогнозам специалистов найдет сбыт 1(2) тысяча изделий. В случае выпуска товаров двумя предприятиями спрос на них распределится в соответствии с данными таблицы:

	A	B	C	D
A	—	40(35)%	70(60)%	90(85)%
B	60(65)%	—	30(25)%	50(50)%
C	30(40)%	70(75)%	—	20(30)%
D	10(15)%	50(50)%	80(70)%	—

т.е. при выпуске товаров A и D, 90(85)% покупателей отдадут предпочтение товару D. Определить оптимальные стратегии руководства предприятий. (В качестве выигрышей взять прогнозируемый спрос (число изделий)).