3. Для отопления помещения необходимо приобрести топливо. Однако, расход топлива и цены на него зависят от погоды в зимнее время:

погода	мягкая	нормальная	суровая
расход, т	6(4)	10(11)	12(13)
цена усл.ед./т	10	16	20

В настоящее время уголь может быть приобретен по минимальной цене 10(15) усл.ед/т и излишек неиспользованного угля можно реализовать весной по цене 5(7) усл.ед/т.

а) Определить оптимальную стратегию в образовании запасов, если известно, что вероятность теплой и холодной зимы практически одинакова, а нормальная зима бывает в 2 раза чаще.

б) Решить задачу а) при условии, что ничего не известно о предстоящей зиме. (использовать критерии Сэвиджа и Гурвица при =).

4. Швейная фабрика по плану должна израсходовать в апреле 35 тыс. Денежных единиц на пошив мужских брюк и костюмов, причем брюки ей обходятся по 10 (12) денежных единиц, а костюм по 25(28). Реализация продукции происходит в мае по следующим ценам: брюки - 20(22), костюм - 45(46). По статистическим данным в мае в прохладную погоду можно продать 500 брюк и 1200 костюмов, в теплую погоду - 2000 брюк и 600 костюмов. Как показала практика, товар, не реализованный в течении месяца, долго лежит на складах и дохода не приносит.

а) Требуется изготовить такое количество товаров, которое максимизирует средний доход фабрики, если по прогнозам погода будет прохладной с вероятностью 0.6(0.7) и 0.4(0.3) - теплой.

б) Решить а), если нет никакой информации о вероятностях состояния природы (использовать критерии Сэвиджа и Гурвица при =).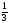

5. Сельскохозяйственное предприятие может посеять одну из 4-х культур A₁, A₂, A₃, A₄. Урожайность культур в центнерах в зависимости от погоды и цена одного центнера каждой культуры дана в таблице.

Погода	Урожайность в центнерах
	A1	A2	A3	A4
сухая	20(18)	7.5(8)	0(2)	3(2.5)
нормальная	5(7)	12.5(14)	7.5(7)	1(1.5)
дождливая	15(12)	5(6)	10(9)	6(5)
цена за центнер	2	4	8	5

Определить какую из культур необходимо посеять для получения максимального дохода, если

а) известны вероятности состояний природы:

Погода	Вероятность
сухая	0.3(0.2)
нормальная	0.4(0.3)
дождливая	0.3(0.5)

б) ничего не известно о вероятностях состояний природы (использовать критерии Сэвиджа и Гурвица при =).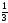

6. На базе организации имеется 3 типа товаров. В магазин должен быть завезен товар одного из типа. Если товар пользуется спросом, то магазин от его продажи получает прибыль, в противном случае несет убытки от его хранения (см. таблицу).

	Тип товара
	1	2	3
Доход от реализации	8(6)	7(9)	9(7)
Убыток при хранении	1(1)	2(3)	3(2)

Известно, что в период продажи спросом будет пользоваться один из трех товаров.

Определить тип товара, который целесообразно завести в магазин, если а) известно распределение вероятностей спроса:

Тип товара	1	2	3
Вероятность спроса	0.25(0.2)	0.4(0.35)	0.35(0.45)

б) распределение вероятностей спроса неизвестно (использовать критерии Сэвиджа и Гурвица при =).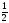

7. Один из 4-х станков должен быть выбран для изготовления партии изделий, размер которой Q может принимать значения: 200(250), 500(450) или 700(600) штук. Производственные затраты C_i для станка i задаются формулой C_i= K_i+c_iQ. Числовые данные для всех станков приведены в таблице:

Станок i	Ki	ci
1	100(110)	5(6)
2	40(50)	12(10)
3	150(120)	3(4)
4	90(80)	8(12)

Необходимо решить задачу выбора станка с целью минимизации затрат, если:

а) известно распределение вероятности размера партии изделий:

Размер партии	200(250)	500(450)	700(600)
Вероятность	0.2(0.25)	0.35(0.4)	0.45(0.35)

б) распределение вероятности размера партии изделий неизвестно (использовать критерии Сэвиджа и Гурвица при =).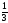

8. Директору одного универмага нужно принять решение о том, какого вида рекламное объявление целесообразно поместить в местной газете. В частности, он может выбрать краткую рекламу или подробную. Еженедельные объемы продаж директор разделяет на 3 группы: средний (А), выше среднего (В) и ниже среднего (С), считая, что объем продаж рассматриваемой недели зависит как от объема продаж предыдущей недели, так и от категории рекламы. Данные о вероятностях объема продаж текущей недели представлены в таблице:

Объем продаж предыду-	Вероятность объема продаж текущей недели
щей недели	краткая реклама				подробная реклама
	В	А	С	В		А	С
В	0.2 (0.15)	0.5 (0.45)	0.3 (0.4)	0.6 (0.55)		0.3 (0.25)	0,1 (0.2)
А	0(0)	0.6(0.55)	0.4(0.45)	0.4(0.35)		0.5(0.5)	0.1(0.15)
С	0(0)	0.3(0.35)	0.7(0.65)	0.2(0.25)		0.7(0.7)	0.1(0.05)

Так, например, если объем продаж предыдущей недели относится к группе А, а используется подробная реклама, то с вероятностью 0.4(0.35) объем продаж текущей недели относится к группе В, с вероятностью 0.5(0.5) - к группе А и с вероятностью 0.1(0.15) - к группе С. Краткая реклама стоит 100(120) долл., а подробная 300(350) долл. и недельная прибыль (без учета затрат на рекламу) при объеме продаж В составит 12(12.5) тыс. долл., при объеме А - 10(9.5) тыс. долл. и при объеме С - 8(7.5) тыс. долл.

а) Определить оптимальные стратегии рекламы в зависимости от объема продаж предыдущей недели, максимизирующие чистую еженедельную прибыль.

б) Определить оптимальные стратегии рекламы, если не известно, какая реклама давалась в предыдущую неделю и, соответственно, не известны вероятности объема продаж текущей недели (использовать критерий Гурвица при =).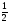

9. Завод приобрел станок стоимостью 100(120) единиц. Для организации ремонта можно приобрести специализированное оборудование стоимостью 50(55) единиц или же обойтись имеющимся ремонтным оборудованием. Если станок выходит из строя, его ремонт с помощью специализированного оборудования обходится в 10(9) единиц. Ремонт без специализированного оборудования обходится в 40(45) единиц. Известно, что в течение срока эксплуатации станок выходит из строя не более 3-х раз. Определить целесообразность приобретения специализированного оборудования, если

а) известно: вероятность того, что станок не выйдет из строя, равна 0,3; выйдет из строя один раз - 0,4; два раза - 0,2; три раза - 0,1.

б) нет информации о вероятностях выхода станка из строя (использовать критерии Сэвиджа и Гурвица при =).

10. Выпуск продукции завода зависит от двух видов деталей, производство которых в местных условиях не представляется возможным. Завод заключил контракты с двумя поставщиками, однако нет гарантии своевременной поставки. Если поставка первого вида детали не прибывает в срок, завод несет убыток в 600(700) усл.ед., второго вида - 500(650) усл.ед. Завод имеет возможность отправить транспорт к одному из поставщиков, в этом случае доставка деталей гарантирована. Расходы поездки составляют 30(60) усл.ед. - к первому поставщику, 50(55) усл.ед. - ко второму. Определить оптимальную стратегию руководства завода, если

а) известны вероятности своевременной доставки: первым поставщиком - 0.8(0.7), вторым - 0.7(0.8) (считаем, что доставка деталей двумя поставщиками - события независимые )

б) не известны вероятности своевременной поставки (использовать критерии Сэвиджа и Гурвица при =).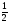

11. Принимается решение о вложение средств (10 тыс. долл.) в одну из отраслей: облигации правительственного займа, военную промышленность или торговлю. Возможны следующие ситуации:

1. изменение курса в сторону смягчения налоговой политики правительства;

1. изменение курса в сторону ужесточения налоговой политики правительства;

2. смена правительства.

Ожидаемый доход от облигаций составляет 10%(10.5%) и не зависит от налоговой политики, однако при смене правительства все его обязательства теряют силу. Доход от вложений в военную промышленность составит 8%(8.5%), не зависит от налоговой политики, но при смене правительства ожидаемый доход увеличивается в 2(1.5) раза. Доход от вложений в торговлю при различных ситуациях составит:

1. смягчение налоговой политики правительства - 12%(11.5%);

2. ужесточение налоговой политики правительства - 8%(7.5%):

3. смена правительства - 6%(5.5%).

Определить отрасль вложения средств, если

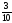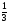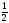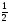а)известны вероятности возникновения ситуаций: a)(), b)(), c)().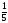

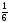б) вероятности возникновения ситуаций не известны (использовать критерии Сэвиджа и Гурвица при =).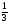

12. Химический комбинат может производить два вида продукции. В начале каждого месяца принимается решение о том, какой вид продукции производить в данном месяце. Принимаемое решение целиком определяется спросом. Спрос имеет случайный характер, причем если в текущем месяце изготовляется продукт вида 1, то в следующем месяце с вероятностью 0.2(0.3) окажется необходимым продолжать изготовление этого продукта и с вероятностью 0.8(0.7) - переключаться на изготовление продукта вида 2. Если же в текущем месяце выпускается продукт вида 2, то в следующем месяце с вероятностью 0.6(0.8) придется продолжать выпуск этого продукта и с вероятностью 0.4(0.2) - переключаться на выпуск продукта вида 1. Для борьбы с загрязнением окружающей среды используют один из трех процессов очистки. Уровень загрязнения при производстве продуктов и использовании процессов очистки представлен в таблице:

	процесс 1	процесс 2	процесс 3
продукт вида 1	80(60)	30(20)	20(30)
продукт вида 2	20(10)	25(40)	50(20)

Для подготовки к началу каждого из процессов очистки необходимо достаточно длительное время, поэтому вопрос о том, какой процесс очистки будет использоваться в данном месяце, приходится решать в начале предыдущего месяца.

а) Определить, какой процесс необходимо использовать в зависимости от вида продукта в текущем месяце.

б) Решить а) при неизвестном распределении вероятностей спроса. (использовать критерий Севиджа и Гурвица при =).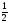

4