5.1.4. Двухбарабанный привод с индивидуальными двигателями

При одинаковых диаметрах барабанов соотношение окружных тяговых сил барабанов пропорционально соотношению мощностей двигателей. Минимально допустимое натяжение ленты по сцеплению при заданной тяговой силе

.

При жестких механических характеристиках двигателей и разных диаметрах барабанов распределение нагрузки между ними существенно меняется.

Тяговую силу, необходимую для перемещения ветвей ленто, можно создать любым из рассмотренных приводных блоков, но требуемое для работы без срыва сцепления натяжение ленты каждого из приводов различно. Меньшего натяжения ленты требуют более сложные конструкции приводов - двухбарабанные с дифференциальным редуктором или с индивидуальными двигателями. Однако целесообразность использования того или иного привода зависит от конкретных условий эксплуатации и определяется тяговыми расчетами (раздел 7). Например, в тех случаях, когда натяжение ленты на приводе создается составляющей силы тяжести перемещаемого груза, необходимости в применении сложных и дорогих приводов нет.

5.2. Ведущие звездочки

Характерной особенностью передачи тяговой силы зацеплением является неравномерность движения цепи, что ограничивает номинальную скорость движения цепи. Оценим изменение скорости движения цепи за один оборот ведущей звездочки, пренебрегая незначительными вертикальными перемещениями цепи.

Дано: расчетная схема (рис. 5.5); 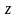- число граней звездочки; 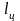- длина граней з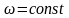вездочки; - частота вращения звездочки.

Определить: характер изменения скорости движения и ускорения цепи во времени.

Каждый зуб звездочки является ведущим при повороте ее на угол .

Время 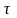поворота звездочки на угол является периодом зацепления.

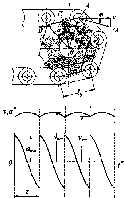
Рис. 5.5. Кинематические параметры передачи тяговой силы зацеплением

Уравнение движения цепи имеет вид:

. (5.16)

При постоянной угловой скорости угол для любого положения ведущего радиуса звездочки

, (5.17)

тогда

. (5.18)

Дифференцируя уравнение (5.18) по времени, получим

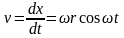. (5.19)

т.е, скорость точки А центра шарнира цепи в функции угла поворота звездочки изменяется по косинусоиде.

Угол изменяется от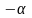 в начале зацепления шарнира до 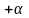в конце зацепления.

В начале периода зацепления

В середине периода зацепления

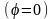
. (5.21)

В конце периода зацепления

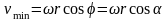. (5.22)

Период зацепления одного шарнира равен времени перемещения цепи на длину грани звездочки (шага цепи)

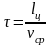, (5-23)

где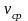 - средняя скорость движения цепи.

Если период одного оборота звездочки Т, то

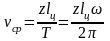, (5.24)

т.е. средняя скорость цепи пропорциональна числу граней звездочки, частоте ее вращения и шагу цепи. Ускорение цепи

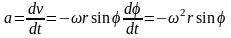, (5.25)

т.е. ускорение изменяется по синусоиде.

При 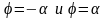ускорение имеет наибольшее по абсолютной величине значение

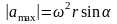. (5.26)

Согласно рис. 5.5 из ΔВОС .

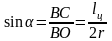Тогда, подставляя в (5.26) 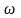из (5.24), получим

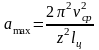, (5.27)

т.е. пропорционально квадрату скорости движения цепи.

Неравномерность движения цепи является источником динамических нагрузок. С ростом скорости движения возрастают удары при входе в зацепление очередного шарнира и износ трущихся частей. Вследствие этого скорость движения цепи ограничивают значениями 1,2... 1,5 м/с выбором соответствующего передаточного отношения редуктора.