4.5Приклади
4.5.1 Визначити втрати тиску на тертя по довжині Рl у сталевій трубі круглого перерізу і квадратного перерізу при рівних довжині, площі живого перерізу труб і швидкості руху води. Довжина труби l, площі живого перерізу , середня швидкість руху води , температура води t.
Розв’язування
Для таких даних: l = 100 м; =0,03 м2 ; v =10 м/с; t=20C.
Визначимо еквівалентні діаметри труб:
для труби круглого перерізу
для труби квадратного перерізу
де d, a, – відповідно геометричний діаметр круглої труби, сторона квадрата, змочений периметр; для труби – = р·d , для квадрата = 4·а.
Знайдемо величини d і a :
Отже, для круглої труби dе.кр=d =0,196м; для труби квадратного перерізу dе.кв= а =0,174 м.
Для визначення коефіцієнта гідравлічного тертя знайдемо числа Рейнольдса і відносну шорсткість при ke=0,05мм=5·10-5м (див. табл. Б.1) і =1,01·10-6м2/с (див. табл. А.12):
для труби круглого перерізу
для труби квадратного перерізу
За універсальною формулою Альтшуля
;
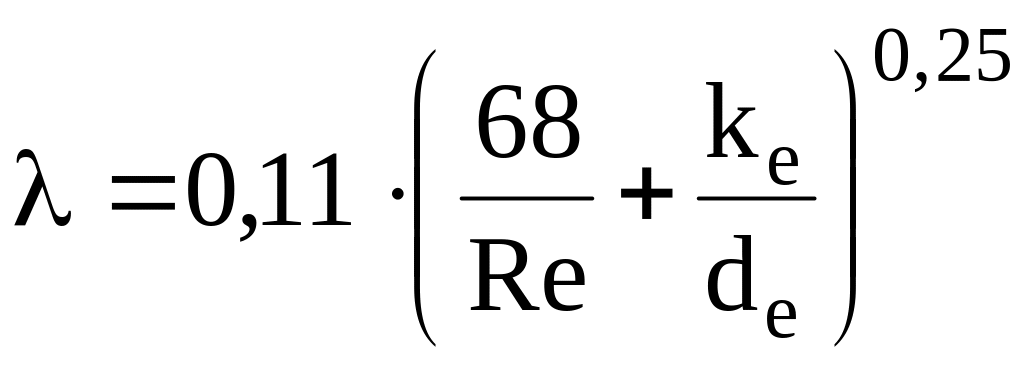для труби круглого перерізу
для труби квадратного перерізу
Втрати тиску на тертя при густині води = 998,2кг/м3 (див. табл. А.12) визначаємо за формулою:
для труби круглого перерізу
;
для труби квадратного перерізу
.
Отже, в трубі квадратного перерізу втрати тиску в 1,18 раза більші, ніж у круглій трубі.
4.5.2. Визначити межове значення швидкості води в трубопроводах теплової мережі, вище якої лінійне зменшення тиску (втрати напору) прямопропорційне квадрату швидкості. Температура води t = 150°С, абсолютна шорсткість труб kе = 5 · 10-4 м.
Розв’язування
Межове значення швидкості води визначаємо за формулою
Кінематичну в’язкість води при t = 150°С знаходимо в табл. А.12
= 0,202 · 10-6 м2/с.
Межова швидкість води в трубах теплової мережі
м/с.
4.5.3 Визначити питоме лінійне зменшення тиску в трубопроводі теплової мережі. Внутрішній діаметр трубопроводу d = 100 мм, температура води t =150°С, швидкість v = 2 м/с, абсолютна шорсткість труб ke = 0,5 мм.
Розв’язування
Питоме лінійне зменшення тиску визначається за формулою
Для того, щоб вибрати розрахункову формулу , необхідно визначити режим руху води за критерієм Рейнольдса
Кінематична в'язкість для води t = 150°С
= 0,202 · 10-6 м2/с (див. табл. А.12)
Оскільки Re>Reгр, то коефіцієнт опору тертя визначається за формулою Шифринсона (4.49)
Густина води при t =150°С в =917 кг/м3. Питоме лінійне зменшення тиску
Па/м.
4.5.4 В круглій трубі довжиною L, діаметром d, витрата рідини G, температура рідини 20 С. Труба нова сталева. Визначити, як зміниться втрата тиску на тертя, якщо замість води з тою ж витратою пропустити касторове масло?
Дано: d = 50 мм, L = 23 м, G = 0,6 кг/с.
Розв’язування
1. З табл. А.4 та табл. А.5 визначаємо теплофізичні властивості рідин при температурі 20 С:
- для води – в = 998 кг/м3; в = 1,0110-6 м2/с;
- для касторового масла – м = 970 кг/м3; м = 10,0210-4 м2/с.
2. Швидкість води в трубі
м/с.
Число Рейнольдса
тобто, режим руху турбулентний.
Коефіцієнт тертя по довжині труби (kе із табл. Б.1)
.
Втрати на тертя при русі води в круглій трубі
Па.
3. Швидкість касторового масла в трубі
м/с.
Число Рейнольдса
,
тобто, режим руху ламінарний.
Коефіцієнт тертя по довжині труби
.
Втрати на тертя при русі касторового масла в круглій трубі
Па.
Втрати на тертя при русі касторового масла в n раз більші ніж при русі води при тій же масовій витраті
.
4.5.5 По трубі діаметром d=0,5 м транспортується вода. В двох точках живого перерізу трубопроводу заміряні швидкості: u = 2,3 м/с на відстані від стінки у = 0,11 м і umax = 2,6 м/с на осі труби. Знайти втрати напору на тертя на 10 м довжини трубопроводу.
Розв’язування
Визначимо коефіцієнт гідравлічного тертя за формулою
логарифмуючи яку, отримаємо:
,
звідки
.
Середню швидкість знаходимо за допомогою залежності
,
м/с.
Втрати напору на тертя визначаємо за формулою Дарсі-Вейсбаха (4.12)
м
на 1 м труби.